3884: 上帝与集合的正确用法
Time Limit: 5 Sec Memory Limit: 128 MBSubmit: 523 Solved: 237
[ Submit][ Status][ Discuss]
Description
根据一些书上的记载,上帝的一次失败的创世经历是这样的:
第一天,
上帝创造了一个世界的基本元素,称做“元”。
第二天,
上帝创造了一个新的元素,称作“α”。“α”被定义为“元”构成的集合。容易发现,一共有两种不同的“α”。
第三天,
上帝又创造了一个新的元素,称作“β”。“β”被定义为“α”构成的集合。容易发现,一共有四种不同的“β”。
第四天,
上帝创造了新的元素“γ”,“γ”被定义为“β”的集合。显然,一共会有16种不同的“γ”。
如果按照这样下去,上帝创造的第四种元素将会有65536种,第五种元素将会有2^65536种。这将会是一个天文数字。
然而,上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来,因此,日复一日,年复一年,他重复地创造着新的元素……
然而不久,当上帝创造出最后一种元素“θ”时,他发现这世界的元素实在是太多了,以致于世界的容量不足,无法承受。因此在这一天,上帝毁灭了世界。
至今,上帝仍记得那次失败的创世经历,现在他想问问你,他最后一次创造的元素“θ”一共有多少种?
上帝觉得这个数字可能过于巨大而无法表示出来,因此你只需要回答这个数对p取模后的值即可。
你可以认为上帝从“α”到“θ”一共创造了10^9次元素,或10^18次,或者干脆∞次。
一句话题意:
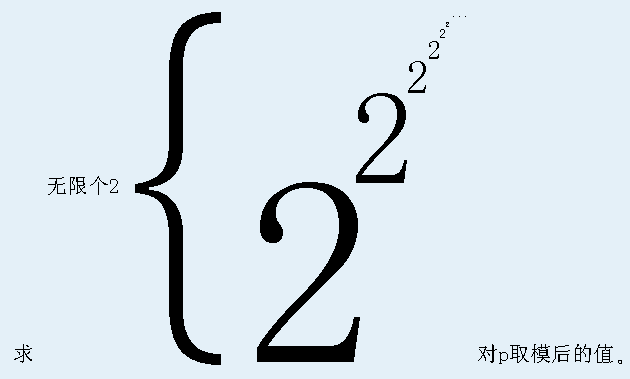
Input
接下来T行,每行一个正整数p,代表你需要取模的值
Output
T行,每行一个正整数,为答案对p取模后的值
Sample Input
3
2
3
6
2
3
6
Sample Output
0
1
4
1
4
HINT
对于100%的数据,T<=1000,p<=10^7
Source
数论题
直接贴 [BZOJ 3884] 上帝与集合的正确用法【欧拉定理/初等数论】 不想列公式了
· Solution 1
我们温习一下欧拉定理:
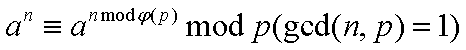
和它的推广:
我们发现,这题的n,p并不一定互素啊,怎么办呢?我们可以让他们强行互素。
利用公式:
我们把原题中的p分为2^k+y
所以原式化为
此时y是奇数,和指数互质了!然后就可以愉快地使用欧拉定理–原式化为
我们发现中间的指数一部分又与原问题相似,于是想到可以递归求解。
那边界是什么呢?我们发现,phi(y)会不断缩小,而且每次至少会除去一个2,所以递归的深度最多为log2(p),当y=1时,返回0即可。
需要事先筛好phi值或者直接需要的时候根号时间计算求解。
复杂度O(p+log2(p))–线性筛/O(log2(p)*sqrt(p))–直接计算。
实践过程中第二种方法远远快于第一种。
· Solution 2
还是根据公式
设答案为f(p),有
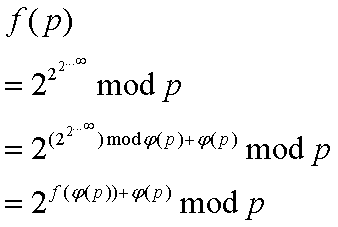
同样递归求解即可,复杂度同第一个解。
发现在模板中沿用至今的sub()居然是错的,666...
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define MAXN (1000000)
typedef long long ll;
ll mul(ll a,ll b,ll F){return (a*b)%F;}
ll add(ll a,ll b,ll F){return (a+b)%F;}
ll sub(ll a,ll b,ll F){return (a-b+llabs(a-b)/F*F+F)%F;}
void upd(ll &a,ll b,ll F){a=(a%F+b%F)%F;}
class Math
{
public:
ll gcd(ll a,ll b){if (!b) return a;return gcd(b,a%b);}
// ll abs(ll x){if (x>=0) return x;return -x;}
ll exgcd(ll a,ll b,ll &x, ll &y)
{
if (!b) {x=1,y=0;return a;}
ll g=exgcd(b,a%b,x,y);
ll t=x;x=y;y=t-a/b*y;
return g;
}
ll pow2(ll a,int b,ll p) //a^b mod p
{
if (b==0) return 1;
if (b==1) return a;
ll c=pow2(a,b/2,p);
c=c*c%p;
if (b&1) c=c*a%p;
return c;
}
ll Modp(ll a,ll b,ll p) //a*x=b (mod p)
{
ll x,y;
ll g=exgcd(a,p,x,y),d;
if (b%g) {return -1;}
d=b/g;x*=d,y*=d;
x=(x+abs(x)/p*p+p)%p;
return x;
}
int h[MAXN];
ll hnum[MAXN];
int hash(ll x)
{
int i=x%MAXN;
while (h[i]&&hnum[i]!=x) i=(i+1)%MAXN;
hnum[i]=x;
return i;
}
ll babystep(ll a,ll b,int p) // a^x = b (mod p)
{
MEM(h) MEM(hnum)
int m=sqrt(p);while (m*m<p) m++;
ll res=b,ans=-1;
ll uni=pow2(a,m,p);
if (!uni) if (!b) ans=1;else ans=-1; //特判
else
{
Rep(i,m+1)
{
int t=hash(res);
h[t]=i+1;
res=(res*a)%p;
}
res=uni;
For(i,m+1)
{
int t=hash(res);
if (h[t]) {ans=i*m-(h[t]-1);break;}else hnum[t]=0;
res=res*uni%p;
}
}
return ans;
}
ll phi(ll x)
{
ll re=x;
for(ll i=2;i*i<=x;i++)
{
if (x%i==0)
{
re=re/i*(i-1);
while (x%i==0) x/=i;
}
}
if (x>1) re=re/x*(x-1);
return re;
}
}S;
int p;
ll calc(ll p)
{
if (p==1) return 0;
ll q=p;
int k=0; while (q%2==0) q/=2,k++;
ll phiQ=S.phi(q);
ll res=(1<<k)*S.pow2( 2LL, sub(calc(phiQ),k,phiQ) ,q );
return res%p;
}
int main()
{
// freopen("bzoj3884.in","r",stdin);
// freopen(".out","w",stdout);
int T;
cin>>T;
while(T--)
{
cin>>p;
cout<<calc(p)<<endl;
}
return 0;
}










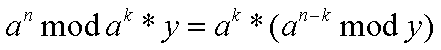
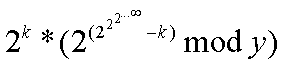
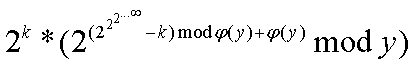
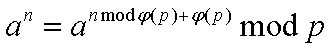














 148
148

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








