Part 4 - Simulation & Base Graphics
Simulation
Generating Random Numbers
Generally, every probability distribution function is associated with four R corresponding functions, which are prefixed with
- d for probability density
- r for random number generation
- p for cumulative distribution
- q for quantile function
Take normal distribution for example, the four functions have the following prototypes:
dnorm(x, mean = 0, sd = 1, log = FALSE)
rnorm(n, mean = 0, sd = 1)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)where the arguments mean and sd (standard deviation) stand for
μ
and
σ
in the normal distribution respectively, which are 0 and 1 by default (i.e. standard normal distribution).
The argument log/log.p implies whether the probabilities p are given as log(p). Lower.tail implies whether the probabilities involved are P[X <= x] or P[X > x].
Assuming the normal distribution to be
f(x)=12π‾‾‾√σe−(x−μ)22σ2
then the cumulative distribution function is
Φ(x)=P(X≤x)=∫x−∞f(t)dt
and the above four functions give the result as follows:
- dnorm(x, μ , σ ) = f(x)
- rnorm(n, μ , σ ) = a numeric vector with n values sampled from f(x)
- pnorm(q, μ , σ ) = P(X≤q) = Φ(q)
- qnorm(p, μ , σ ) = Φ−1(p)
Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known average rate and independently of the time since the last event.
The probability of observing k events in an interval, if they follow Poisson distribution, is given by the equation
P(k)=λkk!e−λ
where
λ
is the average number of events per interval, named the rate parameter.
For Poisson distribution, we have dpois, rpois, ppois and qpois as well. But since Poisson distribution is discrete, dpois(x, λ ) will give a warning and return 0 if x is not an integer.
> rpois(10, 20)
[1] 17 20 16 20 25 16 19 28 27 22
> ppois(6, 2)
[1] 0.9954662
> dpois(1.1, 2)
[1] 0
Warning message:
In dpois(1.1, 2) : non-integer x = 1.100000Reproducibility of random numbers can be achieved by setting identical random seeds with set.seed() function. For others’ convenience to replicate your computation, it is highly recommended to set the seed whenever conducting a simulation.
> set.seed(5)
> rnorm(5)
[1] -0.84085548 1.38435934 -1.25549186 0.07014277 1.71144087
> rnorm(5)
[1] -0.6029080 -0.4721664 -0.6353713 -0.2857736 0.1381082
> set.seed(5)
> rnorm(5)
[1] -0.84085548 1.38435934 -1.25549186 0.07014277 1.71144087Simulating a Linear Model
Suppose we want to simulate from a simple linear model as follows
y=a+bx+ε
where the noise
ε∼N(0,22)
. Now assume
x∼N(0,12)
,
a=0.5
and
b=2
.
> set.seed(20) ## Important for reproducibility
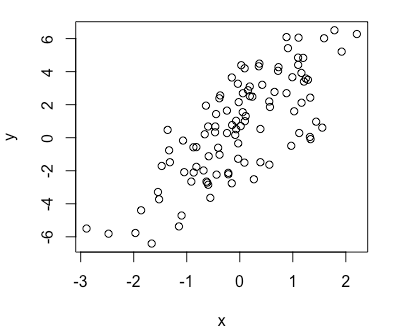
> x <- rnorm(100)
> e <- rnorm(100, 0, 2)
> y <- 0.5 + 2 * x + e
> summary(y)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-6.4080 -1.5400 0.6789 0.6893 2.9300 6.5050
> plot(x, y) ## Plot (x, y) in a graphNow suppose x is binary, either 0 or 1 with 50/50 probability in each trial, then similarly
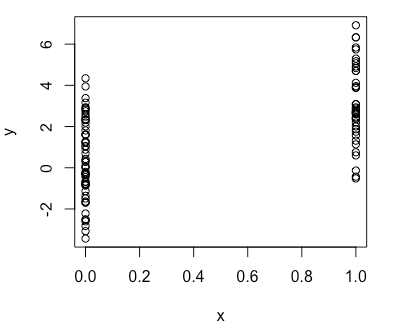
> set.seed(20)
> x <- rbinom(100, 1, 0.5)
> e <- rnorm(100, 0, 2)
> y <- 0.5 + 2 * x + e
> summary(y)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.4360 -0.2675 1.7800 1.5720 2.8810 6.9170
> plot(x, y)Now try simulating from a generalized linear model, e.g. Poisson model.
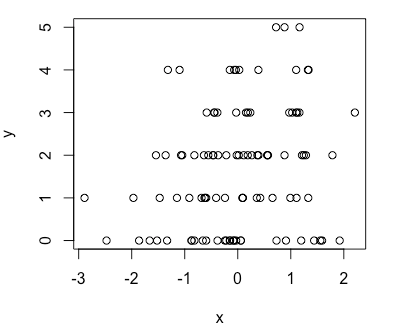
Suppose we have a Poisson model where
y∼Pois(λ)
logλ=a+bx
and assuming
x∼N(0,12)
,
a=0.5
,
b=0.3
. We can simulate it with rpois function.
> set.seed(20)
> x <- rnorm(100)
> log_lambda <- 0.5 + 0.3 * x
> y <- rpois(100, exp(log_lambda))
> summary(y)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 0.00 2.00 1.69 3.00 5.00
> plot(x, y)Note: Almost all of the arguments in functions associated with probability distribution can be vectors EXCEPT one which represents the number of variates to be generated in r* series functions.
E.g. rnorm(5, 1:5, 1:5) produces 5 variates which follow N(1, 1), N(2, 2), …, N(5, 5) respectively.
But rnorm(1:5, 5, 1:5) does not produce the expected result. Mapply(rnorm, 1:5, 5, 1:5) can achieve the desired goal.
Other than normal, Poisson, binomial and uniform distribution, there are a lot more built-in standard distributions, like Bernoull, geometric, hypergeometric, negative binomial, Beta, Gamma, chi-squared, exponential, log-normal, multinomial, Cauchy, F (ratio of two chi-squared), etc.
Random Sampling
The sample() function can be used to draw random samples from arbitrary vectors.
Argument list: sample(x, size, replace = FALSE, prob = NULL)
- x: an arbitrary vector or a single positive integer (treated as 1:x)
- size: number of samples to be drawn, which is the length of x by default
- replace: indicates whether to sample with replacement
- prob: a vector of weights implying the probabilities each element in the vector is to be sampled, no need to sum to one
If only the argument x is assigned, then by default, size is equal to the length of x and replace is set to FALSE, so the sampling result is equivalent to a permutation of the original vector x.
> set.seed(20)
> sample(1:20, 5)
[1] 18 15 6 9 16
> sample(20, 5) ## x = 20 equivalent to x = 1:20
[1] 20 2 19 6 17
> sample(letters, 5) ## Any vector can be sampled from
[1] "s" "z" "a" "r" "e"
> sample(10) ## A permutation of 1:10
[1] 5 3 1 9 10 7 8 2 4 6
> sample(10, replace = TRUE) ## Sample with replacement
[1] 1 10 10 1 7 4 5 9 2 6
> sample(10, 5, replace = TRUE, prob = c(rep(1, 9), 100))
[1] 10 10 10 10 10Base Graphics
All data in the following sections are available here.
Basic Histogram
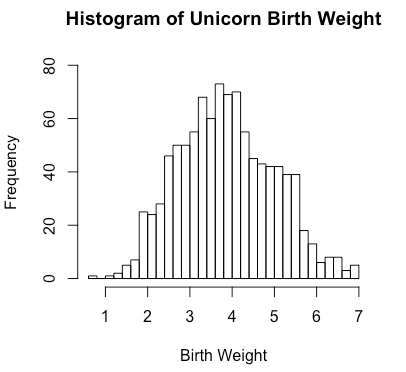
Have a look at our data about birthweight of male and female unicorns.
> unicorns <- read.table("unicorns.txt", header = T)
> head(unicorns)
birthweight sex longevity
1 4.478424 Male 1
2 5.753458 Male 0
3 3.277265 Male 0
4 3.929379 Male 0
5 3.972810 Male 0
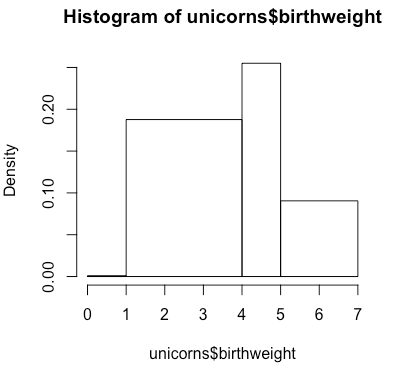
6 4.912954 Male 0We use hist() function to plot a histogram, whose arguments are listed as follows.
> hist(unicorns$birthweight, # Values of x-axis
breaks = 40, # Number of cells
xlab = "Birth Weight", # X-axis label
main = "Histogram of Unicorn Birth Weight", # Plot title
ylim = c(0,80)) # Limits of the y axis (min, max)By default, breaks will be computed according to a particular formula, xlab = vectorName, ylab = “Frequency”, main = “Histogram of” + vectorName.
The argument breaks can also be a vector indicating the breakpoints between the histogram cells.
> hist(unicorns$birthweight, breaks = c(0, 1, 4, 5, 7))Basic Line Graph with Regression
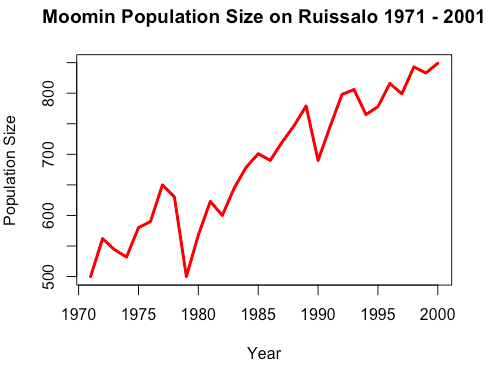
We have data on the population of moomins, a common pest species in Finland, on the island of Ruissalo from 1971 to 2001.
> moomins <- read.table("Moomin Density.txt", header = T)
> head(moomins)
Year PopSize
1 1971 500
2 1972 562
3 1973 544
4 1974 532
5 1975 580
6 1976 590> plot(moomins$Year, moomins$PopSize, # X variable and y variable
type = "l", # Draw a line graph
col = "red", # Line colour
lwd = 3, # Line width
xlab = "Year", # X-axis label
ylab = "Population Size", # Y-axis label
main = "Moomin Population Size on Ruissalo 1971 - 2001")
# Plot titleType indicates which type of plot should be drawn. Some possible options are “p” for points, “l” for lines, “b” for lines covered by points, “o” for lines not covered by points.
Lty (line type) argument controls the type of lines, e.g. “solid“, “dashed”, “dotted”, etc.
Col argument specifies the line color. Numbers can be colors too!
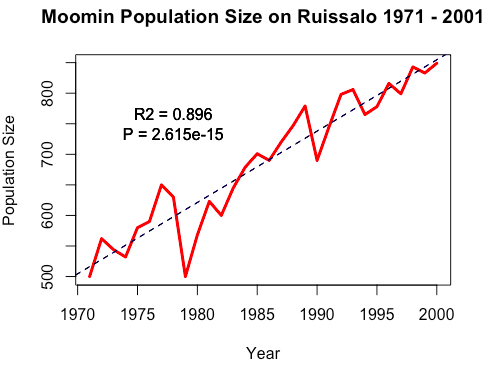
To show the population trend over these years, we can add a basic linear regression to the plot using abline().
> fit <- lm(PopSize ~ Year, data = moomins)
> abline(fit, lty = "dashed")
> text(x = 1978, y = 750, labels = "R2 = 0.896\nP = 2.615e-15")Abline() function also supports the arguments of lty, lwd, col, etc.
Text() function adds texts to the plot at the specified (x, y) coordinates.
Scatterplot with Legend
In this section, we make use of a built-in dataset named iris.
> data("iris")
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
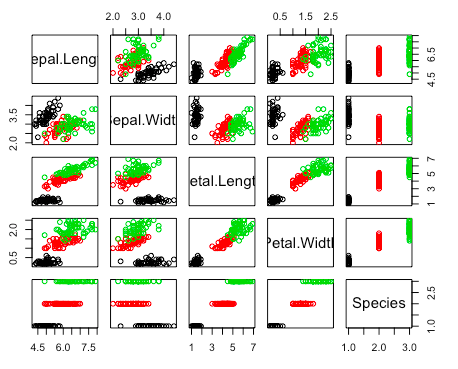
6 5.4 3.9 1.7 0.4 setosaUse pairs() function to see plots on every two variables. We specify different colors of points according to their species.
> pairs(iris, col = iris$Species)Now we come to produce a scatterplot on Sepal.Length and Petal.Length.
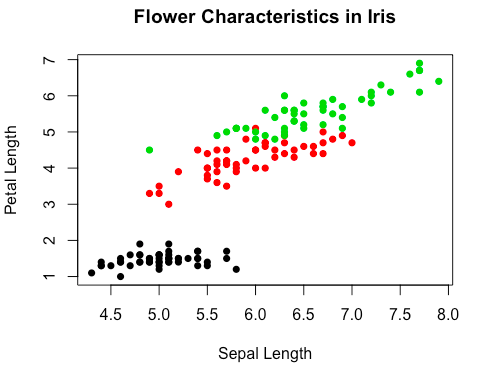
> plot(iris$Sepal.Length, iris$Petal.Length, # X variable, y variable
col = iris$Species, # Color by species
pch = 16, # Type of points
cex = 1, # Size of points
xlab = "Sepal Length", # X-axis label
ylab = "Petal Length", # Y-axis label
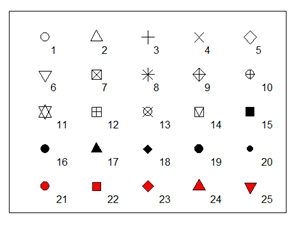
main = "Flower Characteristics in Iris") # Plot titlePch argument specifies a particular type of point, usually by a number index or a character (e.g. “A”).
The list of indexed point types follows.
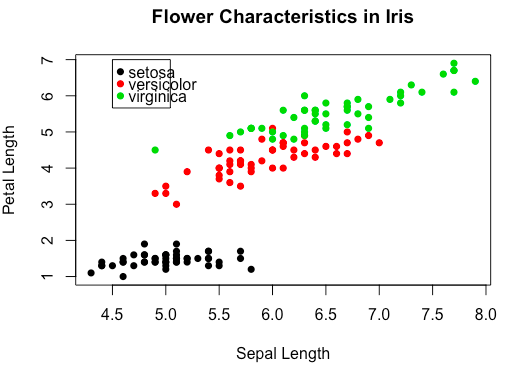
To tell these points apart, we’d better add a legend to the plot.
> legend(x = 4.5, y = 7, legend = levels(iris$Species), col = 1:3, pch = 16)Note 1: It is possible to specify colors to the data frame.
Note 2: It is possible to specify lines in the legend by using lty instead of pch.
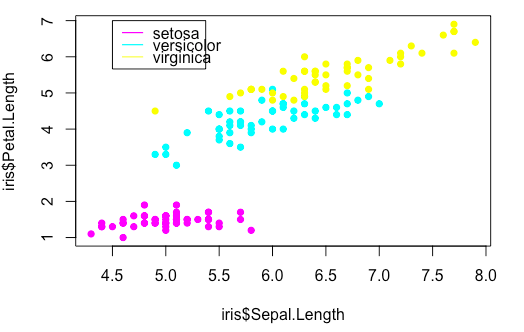
> iris$Colour <- ""
> iris$Colour[iris$Species == "setosa"] <- "magenta"
> iris$Colour[iris$Species == "versicolor"] <- "cyan"
> iris$Colour[iris$Species == "virginica"] <- "yellow"
> plot(iris$Sepal.Length, iris$Petal.Length,
col = iris$Colour, pch = 16, cex = 1)
> legend(x = 4.5, y = 7,
legend = levels(iris$Species),
col = c("magenta", "cyan", "yellow"),
lty = "solid")Boxplot with Reordered and Formatted Axes
Let us continue with the iris dataset.
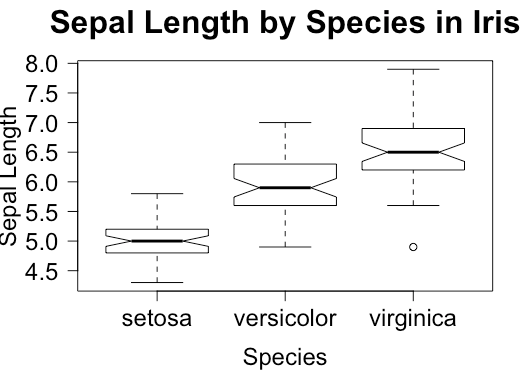
> boxplot(iris$Sepal.Length ~ iris$Species, # x variable, y variable
notch = T, # Draw notch
las = 1, # Orientate the axis tick labels
xlab = "Species", # X-axis label
ylab = "Sepal Length", # Y-axis label
main = "Sepal Length by Species in Iris", # Plot title
cex.lab = 1.5, # Size of axis labels
cex.axis = 1.5, # Size of the tick mark labels
cex.main = 2) # Size of the plot titleIn a boxplot, the bottom and top of the box are always the first and third quartiles, and the band inside is the median. But the ends of whiskers can represent some alternative values, among which the minimum and the maximum are the most common.
Notch argument allows you to compare the medians of the boxplot.
Las argument allows you to rotate the labels of axis.
Cex.lab, cex.axis and cex.main allows you to specify the size of labels, axes and the title respectively.
To reorder the species list in the label, we can reorder it by specifying a particular order like the following command.
iris$Species <- factor(iris$Species, levels = c("virginica", "versicolor", "setosa"))Barplot with Error Bars :(
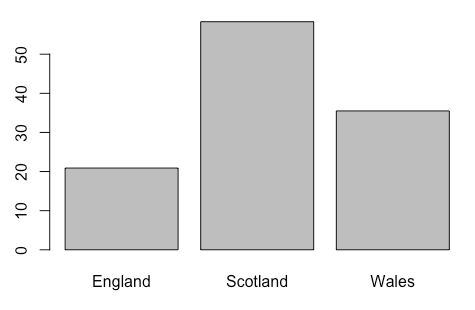
Drawing barplots with base graphics is not that comfortable.
> dragons <- data.frame(
TalonLength = c(20.9, 58.3, 35.5),
SE = c(4.5, 6.3, 5.5),
Population = c("England", "Scotland", "Wales"))
> dragons
TalonLength SE Population
1 20.9 4.5 England
2 58.3 6.3 Scotland
3 35.5 5.5 Wales
> barplot(dragons$TalonLength, names = dragons$Population)But it is really COMPLICATED to draw a barplot with error bars!
Limitations of Base Graphics
You could feasibly do anything you require in base graphics, but some common actions are not straightforward, such as
- Legends
- Dodged plots
- Faceting
- Error bars
- Formatting axes and plot area
Base graphics are best for quick, simple and exploratory graphics, but they are really time-consuming when it comes to complex graphs.
It is HIGHLY RECOMMENDED to use ggplot2 for statistical graphics.
Advantages of ggplot2:
- Consistent underlying grammar of graphics (Wilkinson, 2005)
- Plot specification at a high level of abstraction
- Very flexible
- Theme system for polishing plot appearance
- Mature and complete graphics system
- Many users, active mailing list
A blog on introduction to ggplot2 will come out this summer.






















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








