线性代数 - 高斯消元解线性方程组 + 高斯消元解异或线性方程组

线性代数 - 高斯消元解线性方程组 + 高斯消元解异或线性方程组

1、高斯消元解线性方程组

输入一个包含n个方程n个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含m个方程n个未知数的线性方程组示例：

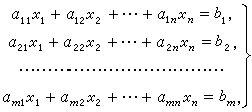
输入格式
第一行包含整数n。

接下来n行，每行包含n+1个实数，表示一个方程的n个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共n行，其中第i行输出第i个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出“Infinite group solutions”。

如果给定线性方程组无解，则输出“No solution”。

数据范围
1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过100。

输入样例：
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例：
1.00
-2.00
3.00

---

分析：

$对给定的增广矩阵进行初等变换，得到矩阵的行最简形式。$

$再从矩阵的最后一行开始倒推每个解。$

$①、无解：系数行列式为0。$

$②、唯一解：线性方程组的矩阵的列是满秩的。$

$③、无穷解：线性方程组的矩阵的列不是满秩的。$

具体落实：

$①、枚举每一列c，找到绝对值最大的一行。$

$②、将该行与第一行交换。$

$③、该行的第一个数变成1。$

$④、将这个1同一列的下面的数都减为0。$

$⑤、判断矩阵的最简形式，倒推把一列只消除剩下一个1，最后的解就是增广矩阵的最后一列。$

代码：

#include<iostream>
#include<cmath>

using namespace std;

const int N=110;
const double eps=1e-6;

int n;
double a[N][N];

int gauss()
{
    int c,r;
    for(c=0,r=0;c<n;c++)
    {
        int t=r;
        for(int i=r;i<n;i++)
            if(fabs(a[i][c])>fabs(a[t][c])) 
                t=i;
                
        if(fabs(a[t][c])<eps) continue;   //若该列已全0，则无需操作
        
        for(int i=c;i<=n;i++) swap(a[t][i],a[r][i]);
        for(int i=n;i>=c;i--) a[r][i]/=a[r][c];   //该列第一个数变成1，整行都缩小a[r][c]倍，从后向前推
        
        for(int i=r+1;i<n;i++)
            if(fabs(a[i][c])>eps)   //将该列其他行的数清0
                for(int j=n;j>=c;j--)
                    a[i][j]-=a[r][j]*a[i][c];
        
        r++;
    }
    
    if(r<n)   //上三角矩阵的行数小于n，系数矩阵不满秩，不是唯一解
    {
        for(int i=r;i<n;i++)
            if(fabs(a[i][n])>eps) return 2;   //此时r行以后的系数矩阵部分全0，若增广矩阵的最后一列对应的值非0，说明矛盾，即无解
        return 1;
    }
    
    for(int i=n-1;i>=0;i--)
        for(int j=i+1;j<n;j++)
            a[i][n]-=a[j][n]*a[i][j];  //从后往前把每一列只消除了剩下一个1
            
    return 0;
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<=n;j++) 
            cin>>a[i][j];
            
    int t=gauss();
    
    if(t==0) 
        for(int i=0;i<n;i++) printf("%.2lf\n",a[i][n]);
        
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
    
    return 0;
}

---

2、高斯消元解异或线性方程组

输入一个包含n个方程n个未知数的异或线性方程组。

方程组中的系数和常数为0或1，每个未知数的取值也为0或1。

求解这个方程组。

异或线性方程组示例如下：

M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中“^”表示异或(XOR)，M[i][j]表示第i个式子中x[j]的系数，B[i]是第i个方程右端的常数，取值均为0或1。

输入格式
第一行包含整数n。

接下来n行，每行包含n+1个整数0或1，表示一个方程的n个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共n行，其中第i行输出第i个未知数的解。

如果给定线性方程组存在多组解，则输出“Multiple sets of solutions”。

如果给定线性方程组无解，则输出“No solution”。

数据范围
1≤n≤100

输入样例：
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例：
1
0
0

---

分析：

$与第一题相似，仅仅在消‘0’的过程从减法变成了异或。$

代码:

#include<iostream>
#include<algorithm>

using namespace std;

const int N=110;

int n,a[N][N];

int gauss()
{
    int c,r;
    for(c=0,r=0;c<n;c++)
    {
        int t=r;
        for(int i=r;i<n;i++)
            if(a[i][c])
                t=i;
        
        if(!a[t][c]) continue;
        
        for(int i=c;i<=n;i++) swap(a[r][i],a[t][i]);
        for(int i=r+1;i<n;i++)
            if(a[i][c])
                for(int j=n;j>=c;j--)
                    a[i][j]^=a[r][j];
                    
        r++;
    }
    
    if(r<n)
    {
        for(int i=r;i<n;i++)
            if(a[i][n]) 
                return 2;
        return 1;
    }
    
    for(int i=n-1;i>=0;i--)
        for(int j=i+1;j<n;j++)
            a[i][n]^=a[i][j]*a[j][n];
    
    return 0;
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n+1;j++)
            cin>>a[i][j];
    
    int t=gauss();
    
    if(t==0) 
        for(int i=0;i<n;i++) cout<<a[i][n]<<endl;
        
    else if(t==1) puts("Multiple sets of solutions") ;
    else puts("No solution");
    
    return 0;
}