“傻瓜”学计量——面板数据1（数据分类）（模型选择？混合vs固定vs随机）

提纲：

1.数据分类

2.模型选择？：混合模型、固定效应模型和随机效应模型

1 数据分类：

1.1 时间序列数据

定义：是指同一个指标按照时间顺序记录的数据列。在同一数据列中各个数据必须是同口径的，要求可比性。

1.2 横截面数据

定义：横截面数据是在同一时间，不同统计单位相同统计指标组成的数据列。

1.3 面板数据

定义：时间序列上取多个截面，在这些截面上同时选取样本观测值所构成的样本数据。

例子：一年内每天所有a股的开盘价（注：要是同一个指标）

优点：可以控制个体异质性

           提供更多信息（20%人是B站活跃用户。每个人的概率为20%or只有20%的人活跃）

缺点：收集 困难

           自选择问题

分类：

平衡面板数据	非平衡面板数据
数据完整	数据部分缺失。补全：不随时间变化的数据

长面板数据	短面板数据
i个体  >  t时间  短面板数据

动态面板模型	静态面板模型
包含被解释变量的滞后值，即往期值

伪面板数据	轮换面板数据
要用的是“个体”特征值， 实际用整个群体的特征值来表示	每个时间所统计的个体中， 都有一定量的个体被新的个体替换

2 面板模型

---

总结（放前面啦）

不同面板模型的区别

如何选用合适的模型

---

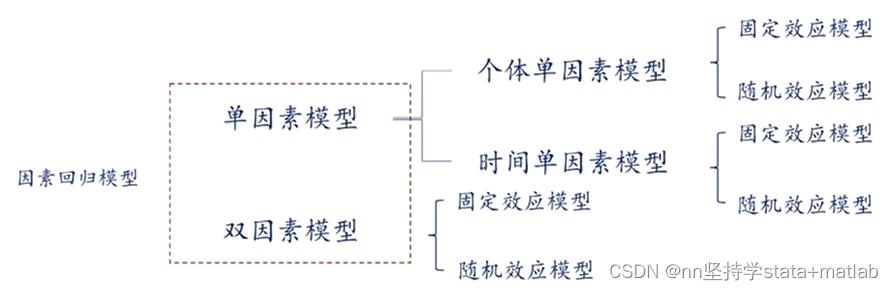
2.1 混合模型Pooled model

不存在个体和时间不可观测因素，即：

2.2 固定效应模型：

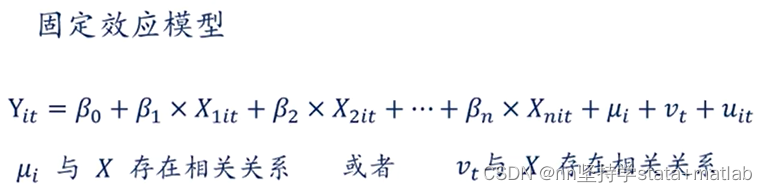
举个不恰当的例子：

μi与X存在相关关系：例如一位“少数民族“up主，天生就会比产出流量相对较高的视频，这就会影响自变量”视频质量”，从而影响Y;

Vt与X存在相关关系：2008年奥运会，导致同一时产出相关内容的视频播放量普遍增长。

2.3 随机效应模型

（以上三种，均假设“自变量X对因变量Y的影响，对每个个体都是一样的，即系数都相同）

2.4 变系数模型

系数不都相同

资料来源：

面板数据4 模型简介：混合模型、固定效应模型和随机效应模型_哔哩哔哩_bilibili