我的java算法:
import java.util.Arrays; /** * Created by Administrator on 2018/4/21. */ public class CityTravel { static int cityCount = 4; //城市数量 static int maxstep = cityCount -1; //城市数量 int shortestval = Integer.MAX_VALUE; //最小的值 int[] shortestarr = new int[cityCount]; //最小的集合 int stepval = 0; int[] steparr = new int[cityCount]; int[] choosecity = new int[cityCount]; int[][] citydistanceArr = null; public void travel(int step){ if(step >= maxstep+1){ //表示走完了所有城市 if(stepval < shortestval){ shortestarr = Arrays.copyOf(steparr,4); shortestval = stepval; System.out.println("当前最短长度是" + shortestval + ",路线是 " + Arrays.toString(shortestarr)); } return; } //继续下一步 for(int i = 0; i < cityCount ; i++){ //下一步没有走过,并且可达,则选中 if(choosecity[i] == 0 && citydistanceArr[steparr[step-1]][i] != -1){ steparr[step] = i; stepval += citydistanceArr[steparr[step-1]][i]; choosecity[i] = 1; travel(step+1); //这里是退回到上一步 steparr[step] = -1; choosecity[i] = 0; stepval -= citydistanceArr[steparr[step-1]][i]; } } } public static void main(String[] args) { int[][] citydistanceArr = new int[cityCount][cityCount]; citydistanceArr[0][0] = -1; citydistanceArr[0][1] = 30; citydistanceArr[0][2] = 6; citydistanceArr[0][3] = 4; citydistanceArr[1][0] = 30; citydistanceArr[1][1] = -1; citydistanceArr[1][2] = 5; citydistanceArr[1][3] = 10; citydistanceArr[2][0] = 6; citydistanceArr[2][1] = 5; citydistanceArr[2][2] = -1; citydistanceArr[2][3] = 20; citydistanceArr[3][0] = 4; citydistanceArr[3][1] = 10; citydistanceArr[3][2] = 20; citydistanceArr[3][3] = -1; CityTravel cityTravel = new CityTravel(); cityTravel.citydistanceArr = citydistanceArr; for(int i = 0 ; i < cityCount ; i++){ cityTravel.steparr[i] = -1;// key表示第几步,value表示选择的城市,用于表示当前路线 cityTravel.choosecity[i] = 0;//key表示城市编号,value表示是否选择,判断当前路线是否已经存在该城市,用于去重 } //城市编号为 0,1,2,3 //固定第一步走城市0 cityTravel.steparr[0] = 0;// step的值表示走过的城市编号,表示第0步选择城市0 cityTravel.choosecity[0] = 1; cityTravel.travel(1); System.out.println("运行结束================"); System.out.println(" 最短距离 " + cityTravel.shortestval); System.out.println(" 最短路线 " + Arrays.toString(cityTravel.shortestarr)); } }
一、问题描述
某售货员要到若干城市去推销商品,已知各城市之间的路程(或旅费)。他要选定一条从驻地出发,经过每个城市一次,最后回到驻地的路线,使总的路程(或总旅费)最小。
如下图:1,2,3,4 四个城市及其路线费用图,任意两个城市之间不一定都有路可达。
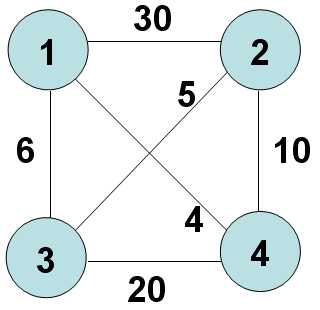
二、问题理解
1.分支限界法利用的是广度优先搜索和最优值策略。
2.利用二维数组保存图信息City_Graph[MAX_SIZE][MAX_SIZE]
其中City_Graph[i][j]的值代表的是城市i与城市j之间的路径费用
一旦一个城市没有通向另外城市的路,则不可能有回路,不用再找下去了
3. 我们任意选择一个城市,作为出发点。(因为最后都是一个回路,无所谓从哪出发)
下面是关键思路:
想象一下,我们就是旅行员,假定从城市1出发,根据广度优先搜索的思路,我们要把从城市1能到达的下一个城市,都要作为一种路径走一下试试。
可是程序里面怎么实现这种“试试”呢?
利用一种数据结构,保存我们每走一步后,当前的一些状态参数,如,我们已经走过的城市数目(这样就知道,我们有没有走完,比如上图,当我们走了四个城市之后,无论从第四个城市是否能回到起点城市,都就意味着我们走完了,只是这条路径合不合约束以及能不能得到最优解的问题)。这里把,这种数据结构成为结点。这就需要另一个数据结构,保存我们每次试出来的路径,这就是堆。
数据结构定义如下:
a.我们刚开始的时候不知道最总能得到的路径是什么,所以我们,就认为按照城市编号的次序走一遍。于是有了第一个结点0,放入堆 中。 相当于来到了城市1(可以是所有城市中的任意一个,这里姑且设为图中城市1)。
b.从城市1,出发,发现有三条路可走,分别走一下,这样就产生了三个结点,都放入堆中。
结点1 数据为:x[1 2 3 4],深度为s=1(深度为0表示在城市1还没有开始走),这说明,结点1是从城市1走来,走过了1个城 市,当前停在城市2,后面的城市3 和城市4都还没有走,但是具体是不是就按照3.4的顺序走,这个不一定。
结点2 数据为:x[1 3 2 4],深度为s=1,表示,从城市1走来,走过了1个城市,当前停在了城市3,后面2.4城市还没走
结点3 数据为:x[1 4 3 2],深度为s=1,表示,从城市1走来,走过了1个城市,当前停在了城市4,后面3.2城市还没有走
c. 从堆中取一个结点,看看这个结点是不是走完了的,也就是要看看它的深度是不是3,是的话,说明走完了,看看是不是能回到起 点,如果可以而且费用少于先前得到最优的费用,就把当前的解作为最优解。
如果没有走完,就继续把这条路走下去。
以上就是简单的想法,而实际的程序中,堆还需要提供对结点的优先权排序的支持。而当前结点在往下一个城市走时,也是需要约束和限界函数,这些书上讲的很清楚,不懂,就翻翻书。
有点要提出来说说的就是结点优先权和限界函数时都用到了一个最小出边和,就相当于把所有城市最便宜的一条路(边)费用加起来的值。
下面是代码
二、代码实现
程序实现了 递归回溯 解决该问题
迭代回溯算法仍在考虑中...
- /****************************************************************
- *问 题:旅行售货员
- *算 法:回溯法
- *描 述:解空间为 排列树
- ****************************************************************/
- #include <stdio.h>
- #define N 4 //城市数目
- #define NO_PATH -1 //没有通路
- #define MAX_WEIGHT 4000
- int City_Graph[N+1][N+1]; //保存图信息
- int x[N+1]; //x[i]保存第i步遍历的城市
- int isIn[N+1]; //保存 城市i是否已经加入路径
- int bestw; //最优路径总权值
- int cw; //当前路径总权值
- int bestx[N+1]; //最优路径
- //-----------------------------------------------------------------
- void Travel_Backtrack(int t){ //递归法
- int i,j;
- if(t>N){ //走完了,输出结果
- for(i=1;i<=N;i++) //输出当前的路径
- printf("%d ",x[i]);
- printf("/n");
- if(cw < bestw){ //判断当前路径是否是更优解
- for (i=1;i<=N;i++){
- bestx[i] = x[i];
- }
- bestw = cw;
- }
- return;
- }
- else{
- for(j=1;j<=N;j++){ //找到第t步能走的城市
- if(City_Graph[x[t-1]][j] != NO_PATH && !isIn[j]){ //能到而且没有加入到路径中
- isIn[j] = 1;
- x[t] = j;
- cw += City_Graph[x[t-1]][j];
- Travel_Backtrack(t+1);
- isIn[j] = 0;
- x[t] = 0;
- cw -= City_Graph[x[t-1]][j];
- }
- }
- }
- }
- void main(){
- int i;
- City_Graph[1][1] = NO_PATH;
- City_Graph[1][2] = 30;
- City_Graph[1][3] = 6;
- City_Graph[1][4] = 4;
- City_Graph[2][1] = 30;
- City_Graph[2][2] = NO_PATH;
- City_Graph[2][3] = 5;
- City_Graph[2][4] = 10;
- City_Graph[3][1] = 6;
- City_Graph[3][2] = 5;
- City_Graph[3][3] = NO_PATH;
- City_Graph[3][4] = 20;
- City_Graph[4][1] = 4;
- City_Graph[4][2] = 10;
- City_Graph[4][3] = 20;
- City_Graph[4][4] = NO_PATH;
- //测试递归法
- for (i=1;i<=N;i++){
- x[i] = 0; //表示第i步还没有解
- bestx[i] = 0; //还没有最优解
- isIn[i] = 0; //表示第i个城市还没有加入到路径中
- }
- x[1] = 1; //第一步 走城市1
- isIn[1] = 1; //第一个城市 加入路径
- bestw = MAX_WEIGHT;
- cw = 0;
- Travel_Backtrack(2); //从第二步开始选择城市
- printf("最优值为%d/n",bestw);
- printf("最优解为:/n");
- for(i=1;i<=N;i++){
- printf("%d ",bestx[i]);
- }
- printf("/n");
- }






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








