刷题笔记：从全排列到二叉树

目录

一、全排列（LeetCode 46）：回溯算法的经典应用 

 二、验证二叉搜索树（LeetCode 98）：BST的中序遍历特性 

三、二叉搜索树中第K小的元素（LeetCode 230）：中序遍历的计数应用

四、二叉树的所有路径（LeetCode 257）：回溯法遍历路径 

总结：算法解题的“套路”与“变通”

---

作为一名算法学习者，最近刷了几道很有代表性的题目，涵盖了回溯算法和**二叉搜索树（BST）**的核心知识点。今天就以这几道题为例，分享一下我的解题思考和代码实现~
 

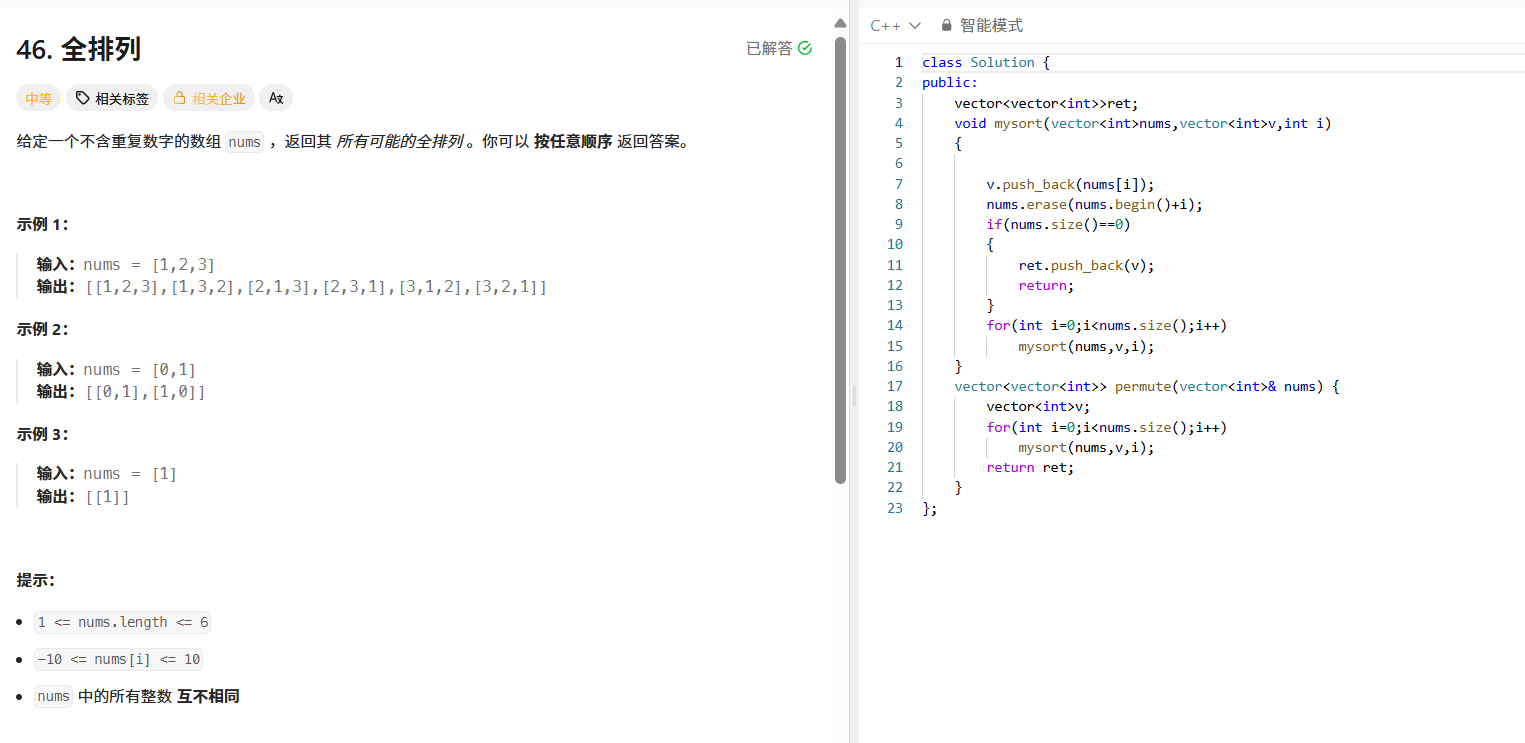
一、全排列（LeetCode 46）：回溯算法的经典应用 

题目分析
 
给定一个不含重复数字的数组，返回其所有可能的全排列。这道题是回溯算法的典型场景——我们需要枚举所有可能的排列组合，每一步选择一个未使用的元素，直到选满所有元素。
 
解题思路
 
- 用一个辅助数组  v  记录当前的排列路径，用原数组  nums  记录剩余可选的元素。
- 每一步从  nums  中选一个元素加入  v ，然后删除该元素（避免重复选择），递归处理剩余元素。
- 当  nums  为空时，说明已经选完所有元素，将当前路径  v  加入结果集。
 
代码实现

class Solution {
public:
    vector<vector<int>> ret;
    void backtrack(vector<int> nums, vector<int> v, int i) {
        v.push_back(nums[i]);  // 选择当前元素
        nums.erase(nums.begin() + i);  // 从剩余元素中删除
        if (nums.size() == 0) {  // 所有元素已选完
            ret.push_back(v);
            return;
        }
        for (int j = 0; j < nums.size(); j++) {  // 递归遍历剩余元素
            backtrack(nums, v, j);
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<int> v;
        for (int i = 0; i < nums.size(); i++) {
            backtrack(nums, v, i);
        }
        return ret;
    }
};
 

关键理解
 
回溯的本质是“选与不选”的决策树遍历，这里通过**修改原数组（删除已选元素）**来控制“不重复选”，确保每一步的决策都是基于剩余元素的。

 二、验证二叉搜索树（LeetCode 98）：BST的中序遍历特性 

题目分析
 
验证一棵二叉树是否是有效的二叉搜索树。BST的定义是：左子树所有节点值严格小于当前节点，右子树所有节点值严格大于当前节点，且左右子树也必须是BST。
 
解题思路
 
BST的中序遍历序列是严格递增的，这是解题的关键！我们可以用中序遍历遍历整棵树，记录前一个节点的值  prev ，如果当前节点值小于等于  prev ，则不是有效BST。
 
代码实现

class Solution {
public:
    long long prev = LLONG_MIN;  // 初始化为long long最小值，避免与int范围冲突
    bool ValidBST(TreeNode* root) {
        if (root == nullptr) return true;
        if (!ValidBST(root->left)) return false;  // 先遍历左子树
        if (root->val <= prev) return false;     // 检查当前节点是否递增
        prev = root->val;                        // 更新prev为当前节点值
        return ValidBST(root->right);            // 遍历右子树
    }
    bool isValidBST(TreeNode* root) {
        return ValidBST(root);
    }
};
 

关键理解
 
中序遍历的“左-根-右”顺序，天然契合BST的“左小右大”特性，通过一个全局变量  prev  就能轻松判断序列是否严格递增。
 

三、二叉搜索树中第K小的元素（LeetCode 230）：中序遍历的计数应用

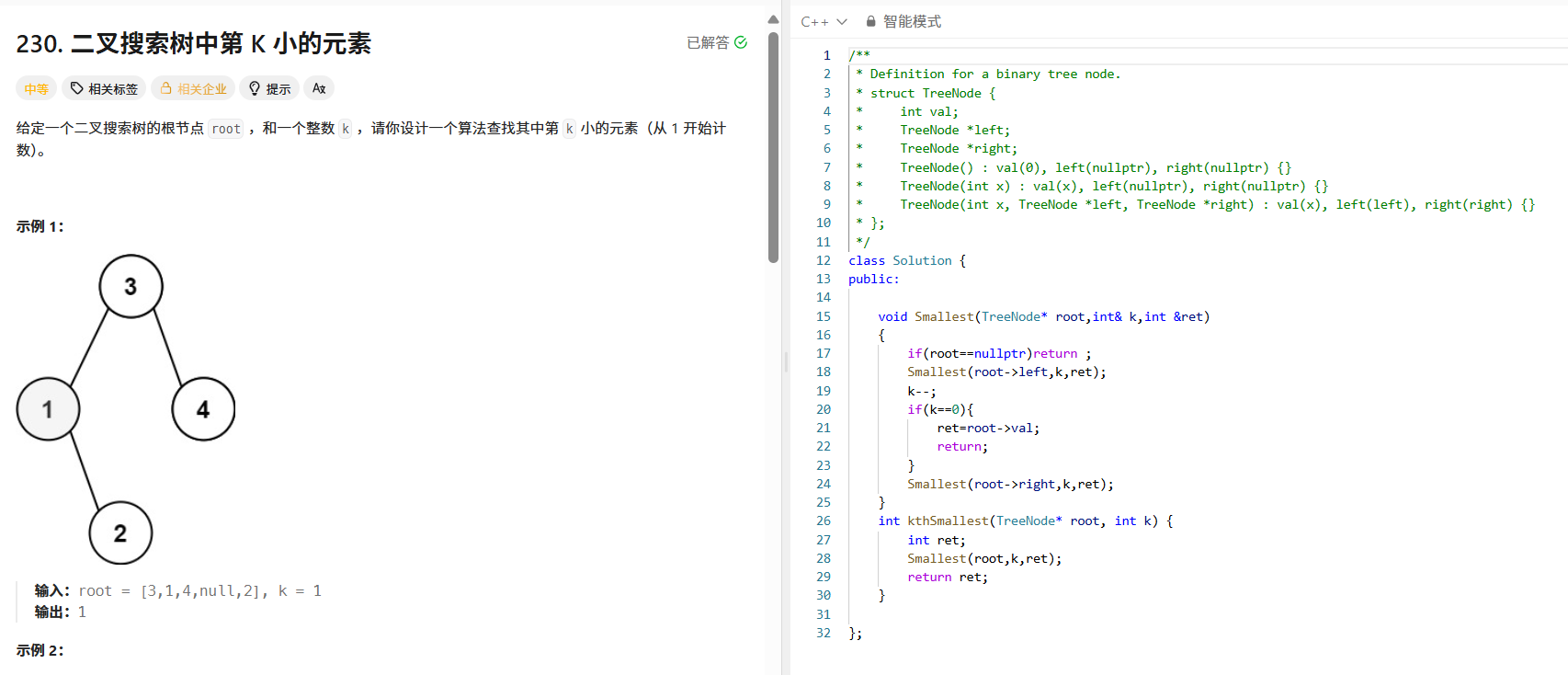
题目分析
 
在BST中找第K小的元素（从1开始计数）。结合BST中序遍历递增的特性，我们可以在中序遍历时进行计数，当计数等于K时，就是目标元素。
 
解题思路
 
- 用中序遍历遍历BST，每访问一个节点就将  k  减1。
- 当  k  减到0时，当前节点的值就是第K小的元素。
 
代码实现

class Solution {
public:
    void findKth(TreeNode* root, int& k, int& ret) {
        if (root == nullptr) return;
        findKth(root->left, k, ret);  // 先遍历左子树（最小的元素在左子树）
        k--;
        if (k == 0) {  // 找到第K小的元素
            ret = root->val;
            return;
        }
        findKth(root->right, k, ret); // 遍历右子树
    }
    int kthSmallest(TreeNode* root, int k) {
        int ret;
        findKth(root, k, ret);
        return ret;
    }
};

关键理解
 
BST的中序遍历是“从小到大”的顺序，所以第1小的是最左节点，第2小的是左子树遍历完后的下一个节点，以此类推，通过递减k并判断是否为0即可精准定位。
 

四、二叉树的所有路径（LeetCode 257）：回溯法遍历路径 

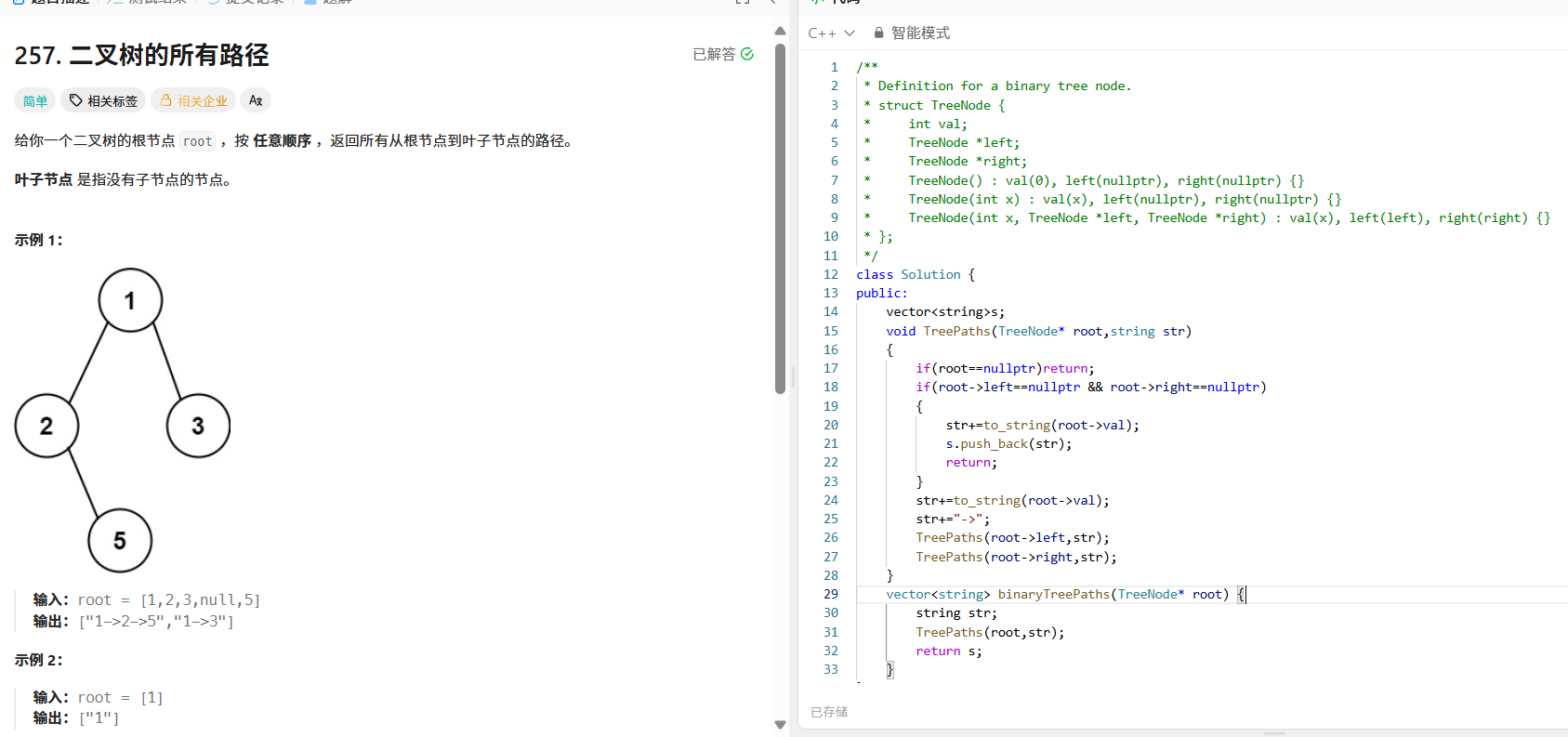
题目分析
 
返回二叉树中所有从根节点到叶子节点的路径。叶子节点是指没有子节点的节点。
 
解题思路
 
这是一道典型的回溯+路径记录题目：
 
- 用一个字符串  str  记录当前路径，每访问一个节点就将其值加入字符串。
- 当遇到叶子节点时，将当前路径加入结果集。
- 递归遍历左右子树，遍历完成后无需“回退”（因为字符串是按值传递的，递归层之间不共享）。
 
代码实现

class Solution {
public:
    vector<string> s;
    void dfs(TreeNode* root, string str) {
        if (root == nullptr) return;
        if (root->left == nullptr && root->right == nullptr) {  // 叶子节点
            str += to_string(root->val);
            s.push_back(str);
            return;
        }
        str += to_string(root->val) + "->";  // 非叶子节点，加入路径并添加箭头
        dfs(root->left, str);
        dfs(root->right, str);
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        string str;
        dfs(root, str);
        return s;
    }
};
 

关键理解
 
路径记录的核心是“走到哪记到哪”，叶子节点是路径的终点，此时将完整路径保存即可。由于字符串是值传递，递归调用时会自动维护不同路径的独立性，无需手动回溯。
 

总结：算法解题的“套路”与“变通”

从这几道题可以看出，经典算法思想是可以复用的：
 
- 全排列和二叉树路径用了回溯法，核心是“选择-递归-撤销选择”（本题中通过数组删除和字符串拼接天然实现了路径的维护）。
- 二叉搜索树的两道题则利用了中序遍历的特性，将BST的结构特性转化为“序列递增”的可量化条件。
 
刷题的关键不是死记硬背代码，而是理解每一种算法思想的适用场景和核心逻辑，这样才能在遇到新题时灵活变通~ 希望这篇笔记能帮到和我一样在算法路上摸索的小伙伴！