炮弹碎片飞行轨迹模拟展示

最新推荐文章于 2024-06-11 19:07:54 发布

西瓜刀盹了

最新推荐文章于 2024-06-11 19:07:54 发布

阅读量747

点赞数

分类专栏：数据结构与算法文章标签：算法

本文链接：https://blog.csdn.net/npu_nazi/article/details/129695466

版权

数据结构与算法专栏收录该内容

4 篇文章

订阅专栏

文章通过物理原理和编程模拟了不同初始角度（30/45/60度）下弹片的飞行轨迹，并运用二分法寻找最大飞行距离对应的初始角度。程序使用Python实现，结合数学和物理知识，计算出在给定条件下的弹片运动路径和最优化角度（约18.57度）。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一. 问题描述

弹片飞行轨迹是多重因素影响的抛物线问题：炸药赋予弹片初速，重力始终控制弹片向地面运动，空气阻力和弹片飞行速度相关，方向始终和弹片飞行方向相反以阻止弹片无限制运动。假设给定弹片初速为 1000m/s，重力加速度为 9.8m/s2，空气阻力系数为-k*v*v（k 为常数，取 0.003 或其他指定数值，v 为弹片当前速度），请给出特定速度方向（30/45/60 度）的弹片飞行轨迹，并算出最大飞行距离时的弹片抛射角度。

二. 结果展示

1. 参数为:初始角度45度时:

2. 初始角度为30度时:

3. 初始角度为60度时:

4. 最远飞行轨迹下的初始角度计算:

计算迭代过程:

初始角度为18.57度时的轨迹展示:

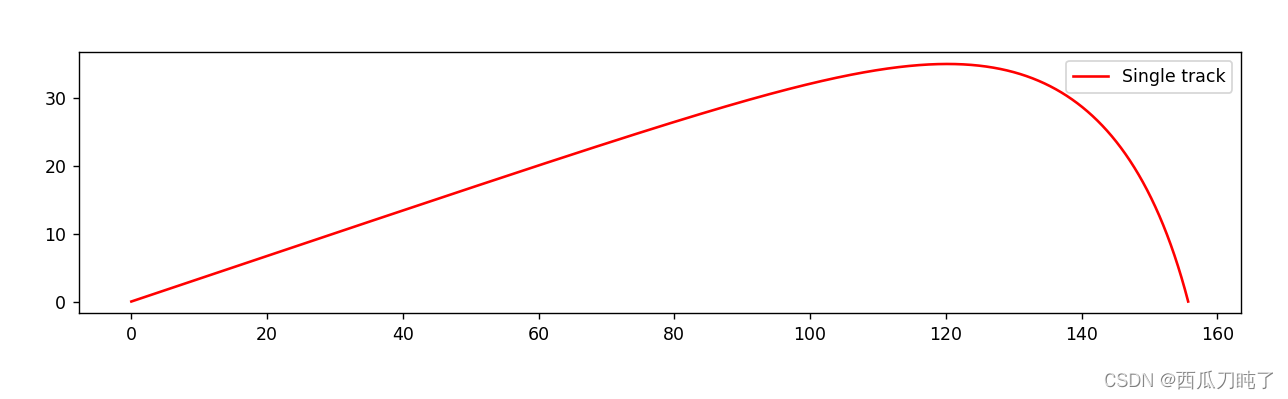
三. 解题思路

1. 使用单步模拟法, 依据物理原理, 计算出每一小步的值,存入list,最后统一输出.

2. 对于最大飞行距离时的弹片抛射角度问题,

首先我们设想, 飞行距离 y 相对于初始角度 x 是一个先增后减的函数, 那么,对于这个函数极值的求解, 可转化为求导后, 零点的求解. 因此, 采用此思想求解.

但是, 实际中还有一些问题, 任何一个初始角度的飞行距离都要进行模拟计算, 如果直接暴力排列,则非常消耗计算资源.(由于我们第一步, step设置为0.0001,即0.0001秒当成一个直线运动,之后重新计算角度, 重新模拟, 精度非常高)因此, 对于此问题, 设计二分斜率查找法.

采用二分斜率查找的方法, 首先设置初始最大角度30°, 最小角度10°, 采用二分法,每一次记录mid角度时, 的最远距离. 此时判断斜率是正还是负, 如果是负的 ,则把up_bound = mid_bound, 反之同理, 同时计算出第二次mid角度时,最远距离,继续迭代判断.

最终设置两次斜率差值小于设置的精度时(0.001), 完成计算, 即最终迭代计算出斜率为0.0001590的时候,终止了迭代,(经过多次尝试,精度再进一步, python 数字精度的损失要大于算法精度的损失, 对于编程语言无法模拟无理数的问题, 目前我也无法解决.)

四. 程序源码

1. 弹片飞行轨迹模拟

import math
import matplotlib.pyplot as plt


def draw(x, y):
    plt.figure(figsize=(12, 6))
    plt.plot(x, y, c='red', label='Single track')
    plt.legend()
    plt.gca().set_aspect(1)
    plt.show()


def main():
    step = 0.0001
    initial_speed = 1000
    initial_angle = 18.57
    g = 9.8
    k = 0.003
    m = 0.1
    # 横纵坐标初1
    # 计算结果
    x_list = [0]
    y_list = [0]
    # 坐标
    x = 0
    y = 0
    v = initial_speed
    v_y = v * math.sin(math.radians(initial_angle))
    v_x = v * math.cos(math.radians(initial_angle))
    angle = math.radians(initial_angle)
    while y >= 0 and v > 0:
        f = k * v * v
        a_f = f / m
        a_f_y = a_f * math.sin(angle)
        a_f_x = a_f * math.cos(angle)

        v_y = v_y - g * step - a_f_y * step
        v_x = v_x - a_f_x * step
        x1 = x + v_x * step
        y1 = y + v_y * step
        x_list.append(x1)
        y_list.append(y1)
        # 更新相关参数
        v = math.sqrt(v_y * v_y + v_x * v_x)
        angle = math.atan((y1 - y) / (x1 - x))

        # if x1 - x > 0:
        #     angle = math.atan((y1 - y) / (x1 - x))
        # else:
        #     angle = math.radians(-90)
        x = x1
        y = y1

    print(x_list)
    print(y_list)
    draw(x_list, y_list)
    print("max_x : " + str(x_list.pop()))


if __name__ == '__main__':
    main()

2. 最远时的角度求解

import math
import matplotlib.pyplot as plt


def draw(x, y):
    plt.figure(figsize=(12, 6))
    plt.plot(x, y, c='red', label='Single track')
    plt.legend()
    plt.show()


def find_dis(angle):
    step = 0.00001
    initial_speed = 1000
    initial_angle = angle
    g = 9.8
    k = 0.003
    m = 0.1
    # 横纵坐标初1
    # 计算结果
    x_list = [0]
    y_list = [0]
    # 坐标
    x = 0
    y = 0
    v = initial_speed
    v_y = v * math.sin(math.radians(initial_angle))
    v_x = v * math.cos(math.radians(initial_angle))
    angle = math.radians(initial_angle)
    while y >= 0 and v > 0:
        f = k * v * v
        a_f = f / m
        a_f_y = a_f * math.sin(angle)
        a_f_x = a_f * math.cos(angle)

        v_y = v_y - g * step - a_f_y * step
        v_x = v_x - a_f_x * step
        x1 = x + v_x * step
        y1 = y + v_y * step
        x_list.append(x1)
        y_list.append(y1)
        # 更新相关参数
        v = math.sqrt(v_y * v_y + v_x * v_x)
        angle = math.atan((y1 - y) / (x1 - x))

        # if x1 - x > 0:
        #     angle = math.atan((y1 - y) / (x1 - x))
        # else:
        #     angle = math.radians(-90)
        x = x1
        y = y1

    # print(x_list)
    # print(y_list)
    # draw(x_list, y_list)
    pop = x_list.pop()
    print("find_dis: x: " + str(initial_angle) + "   dis:  " + str(pop))
    return pop


def find_angle():
    delta = 0.001
    max_x = 0.0
    gradient = 10.0  # 初始斜率,无穷大
    up_bound = 30.0
    low_bound = 10.0
    mid_bound = 20.0
    precision = 0.001
    while abs(gradient) > precision:
        mid_bound = (up_bound + low_bound) / 2
        now_gradient = (find_dis(mid_bound) - find_dis(mid_bound - delta)) / delta
        if now_gradient < 0:
            up_bound = mid_bound
        else:
            low_bound = mid_bound
        print("x: " + str(mid_bound) + "     gradient: " + str(now_gradient))

        if abs(now_gradient) < gradient:
            gradient = abs(now_gradient)
        elif now_gradient == gradient:
            precision /= 10
            delta /= 10
        pass
    print("最小斜率时的x: " + str(mid_bound) + "    斜率: " + str(gradient))


if __name__ == '__main__':
    find_angle()
    pass