开源数学推理模型DeepSeek-Prover-V2：88.9%通过率+超长推理链-CSDN博客

本文链接：https://blog.csdn.net/nulifancuoAI/article/details/147758421

DeepSeek-Prover-V2是由中国深度求索（DeepSeek）团队推出的开源数学推理大模型，包含6710亿参数（671B）和70亿参数（7B）两个版本。该模型专攻数学形式化证明，支持将自然语言问题转化为Lean 4代码并完成逻辑严谨的定理验证，在MiniF2F-test评测中通过率高达88.9%，刷新了AI数学推理的行业纪录。

核心能力亮点：

超长推理链处理：支持163,840 tokens的上下文窗口，可拆解数学奥赛题至20+引理步骤；
双模式解题：快速模式直接生成代码答案，逻辑模式分步拆解推理过程；
低成本部署：7B版本可在RTX 4090显卡运行，推理速度达60 tokens/秒；

AI快站限时免费体验地址：

https://chat.aifasthub.com/

AI快站下载：

https://aifasthub.com/deepseek-ai/DeepSeek-Prover-V2-671B

数据解读DeepSeek-Prover-V2的强大

DeepSeek-Prover-V2的卓越性能并非偶然，其背后是多项技术创新和海量数据训练的支撑。

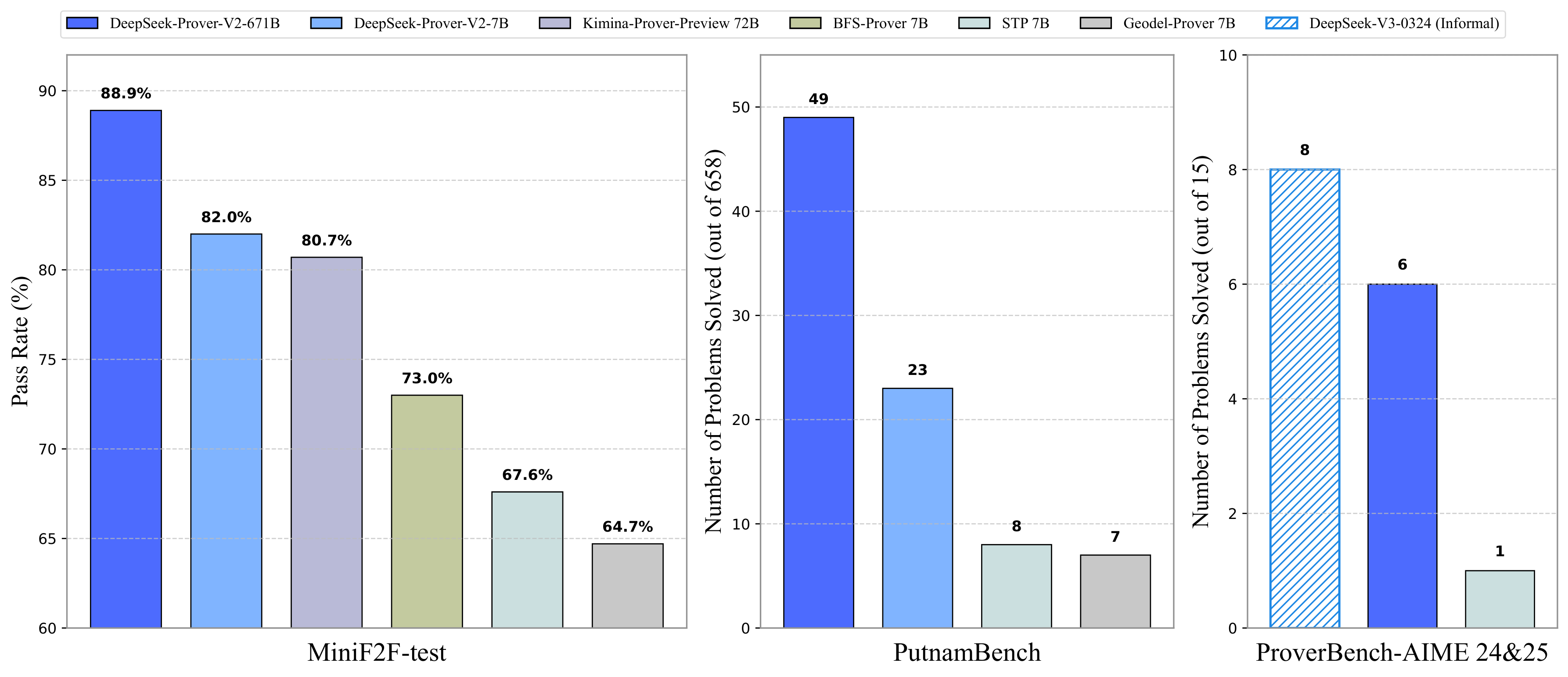
惊人的性能：MiniF2F测试集88.9%通过率

衡量一个数学证明模型的性能，权威的基准测试是关键。在备受关注的 MiniF2F-test 测试集（一个包含奥林匹克级别数学问题的集合）上，DeepSeek-Prover-V2 取得了高达88.9%的通过率！这是一个非常了不起的成绩，意味着该模型能够成功解决绝大多数具有挑战性的形式化数学问题。

例如，在包含488个问题的MiniF2F-test上，DeepSeek-Prover-V2利用其递归证明搜索策略，能够解决434个问题，这一数据充分证明了其在解决复杂数学难题方面的强大实力。

此外，在另一个具有挑战性的 PutnamBench 数据集（包含来自著名的Putnam数学竞赛的问题）上，DeepSeek-Prover-V2 能够解决658个问题中的49个。在更侧重于实际证明场景的 ProofNet 测试集上，该模型在 Pass@1024 指标下实现了 37.1% 的解题率。这些数据共同描绘了DeepSeek-Prover-V2在不同难度和类型的数学问题上的全面能力。

超大规模与先进架构：6710亿参数与MoE设计

DeepSeek-Prover-V2 拥有惊人的 6710亿参数，这使其能够学习和存储海量的数学知识和推理模式。该模型基于 DeepSeek-V3 架构，并采用了先进的混合专家（Mixture-of-Experts, MoE）设计。

具体来说，在其MoE层中，包含了256个路由专家（routing experts）和1个共享专家（shared expert）。在推理过程中，每个token会激活8个专家进行计算。这种设计允许模型在保持巨大参数规模的同时，有效控制推理时的计算量，实现了性能与效率的平衡。

强大的长程推理能力：支持163,840 tokens上下文

数学证明往往涉及冗长而复杂的推理链条。DeepSeek-Prover-V2 支持高达 163,840个tokens的上下文长度，这意味着它可以处理非常长的数学问题描述、背景知识和中间推理步骤，而不会轻易丢失关键信息。这对于解决需要多步推导的复杂定理至关重要。

创新的训练方法：递归定理证明与强化学习

为了提升模型的证明能力，DeepSeek-Prover-V2 采用了创新的训练方法。研发团队设计了一个递归定理证明流程（recursive theorem-proving process），让模型能够像人类数学家一样，将复杂问题分解为子问题，并逐步解决。

更重要的是，该模型还引入了强化学习（Reinforcement Learning）技术。通过将非形式化的数学推理（人类的直觉和草稿）与形式化的证明过程相结合，模型能够在统一的框架下学习和优化其证明策略。这种方法使得模型不仅能理解形式化语言的严谨性，也能借鉴人类解决问题时的灵活性和创造性。

全新的评测基准：ProverBench

为了更全面、更准确地评估数学证明模型的能力，DeepSeek团队还推出了一个全新的评测基准——ProverBench。该基准包含了325个精选的形式化问题，这些问题来源于奥林匹克竞赛、数学出版物以及专门为AI设计的证明题，覆盖了数论、代数、几何等多个数学分支。ProverBench的提出，为该领域的研究者提供了一个更具挑战性和代表性的评估平台。

架构浅析：MoE如何赋能数学推理？

如前所述，DeepSeek-Prover-V2的核心架构优势之一在于其混合专家（MoE）设计。简单来说，MoE可以将一个庞大的神经网络拆分成多个相对较小的“专家网络”。当输入数据（在这里是数学问题或证明步骤）到来时，一个“门控网络”（gating network）会判断哪些专家最擅长处理当前任务，然后将任务分配给这些被选中的专家。

在DeepSeek-Prover-V2中，每层有256个路由专家和1个共享专家。共享专家负责处理一些通用的模式，而路由专家则各自专精于不同类型的数学知识或推理技巧。推理时仅激活8个专家，大大减少了计算负载，使得如此庞大的模型也能在可接受的时间内完成推理。这种“各司其职、协同作战”的方式，使得模型能够更高效地学习和应用广泛的数学知识。