第四章矩阵分解

ouger爱编程

已于 2023-12-08 11:16:42 修改

阅读量85

点赞数

分类专栏：矩阵分析文章标签：矩阵算法线性代数

于 2023-11-17 11:02:03 首次发布

本文链接：https://blog.csdn.net/onlyyoujojo/article/details/134457780

版权

矩阵分析专栏收录该内容

7 篇文章 1 订阅

订阅专栏

矩阵分解

奇异值分解：

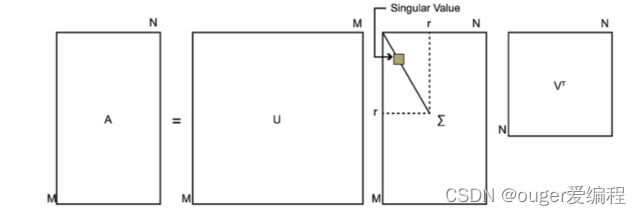
在这里插入图片描述

$U\Sigma V^H\\ \Sigma =\left[ \begin{matrix} \Delta & 0 \\ 0 &0 \end{matrix} \right]$

$U$ 和 $V$ 都是酉矩阵，满足 $U^TU=I,V^TV=I$

$U$ 的列向量就是 $AA^H$ 的标准正交特征向量， $\lambda_i$ 是 $AA^H$ 的特征值

$V$ 的列向量就是 $A^HA$ 的标准正交特征向量， $\mu_i$ 是 $A^HA$ 的特征值，显然特征值分解不唯一（因为特征向量不唯一，特征向量标准正交化时也不唯一）。

其中
$\Delta=\left[ \begin{matrix} \alpha_1 & \\ & \alpha_2 &\\ & &\ddots\\ &&&\alpha_r \end{matrix} \right]$
其中 $r$ 为奇异值个数。 $\alpha_i$ 就是矩阵 $A$ 的奇异值。

因为 $\sqrt{\lambda_i} =\sqrt{\mu_i}=\alpha_i$

所以只需要求出 $A^HA$ 或者 $AA^H$ 里面较为简单的那个矩阵的特征值和特征向量。

如：求出 $A^HA$ 的特征值 $\lambda_i$ 和特征向量 $U_i$ 后，就可以直接求得
$V_i = A^HU_i\Delta^{-1}$
求法：
请添加图片描述

正交三角分解（UR分解）

要求 $A$ 为方阵：
${\large A = UR}， \\其中U是酉矩阵，R是正线上三角矩阵$
直接看计算过程：

第一步：对 $A=[\alpha1,\alpha_2,\dots,\alpha_n]$ 的列向量标准正交化

正交化：
$\begin{align} \beta_1 &= \alpha_1\\ \beta_i &= \alpha_i - \frac{(\alpha_i,\beta_1)}{(\beta_1,\beta_1)}\beta_1- \frac{(\alpha_i,\beta_2)}{(\beta_2,\beta_2)}\beta_2-\dots-\frac{(\alpha_i,\beta_{i-1})}{(\beta_{i-1},\beta_{i-1})}\beta_{i-1} \end{align}$
标准化： $\Large \eta_i=\frac{\beta_i}{||\beta||}$

再找到 $\alpha_i$ 和 $\eta_i$ 之间的数量关系，这是先通过 $\eta_i$ 和 $\beta_i$ ，再通过 $\beta_i$ 和 $\alpha_i$ 找到的。

在这里插入图片描述

谱分解

要求 $A$ 为正规矩阵，即 $A^HA=AA^H$
$\large {\begin{align} A &= [\alpha_1,\alpha_2,\dots,\alpha_n] \left[ \begin{matrix} \lambda_1 & \\ & \lambda_2 &\\ & &\ddots\\ & & &\lambda_n \end{matrix} \right ] \left[ \begin{matrix} \alpha_1^H\\ \alpha_2^H\\ \vdots\\ \alpha_n^H \end{matrix} \right]\\ &=\lambda_1\alpha_1\alpha_1^H + \lambda_2\alpha_2\alpha_2^H + \dots +\lambda_n\alpha_n\alpha_n^H\\ &=\sum_{i=1}^r \lambda_i\sum_{j=1}^{n_i}\alpha_{ij}\alpha_{ij}^H\\\ &=\sum\lambda_i G_i\\ \end{align} }$

计算：

第一步：求 $A$ 的特征值和特征向量 $\large[\alpha_1,\alpha_2,\dots,\alpha_n]$ 。

第二步：将有重根的特征值对应的特征向量正交化。

第三步：把所有特征向量单位化为 $\large[\eta_1,\eta_2,\dots,\eta_n]$

第三步：于是 $\large G_i = \eta_{i1} \eta_{i1}^H + \eta_{i2} \eta_{i2}^H + \dots+\eta_{im} \eta_{im}^H，m为\lambda_i 对应的几何重数$
最后： $A$ = $\large \sum\lambda_iG_i$

谱分解还有一种特殊的情况
当 $A$ 为可对角化的矩阵时，谱分解可以这么来求;

求 $A$ 的特征值，特征向量，得到可逆矩阵 $P$ ， $P^{-1}AP = \Lambda$
求 $(P^{-1})^T=(\beta_1, \beta_2, \dots, \beta_n)$
$G_i = \sum\limits_{j=1}^{m}\alpha_{ij}\beta_{ij}^T$ ，其中 $m$ 为特征值 $\lambda_i$ 对应的代数重数。
原理如下，因为 $\large P^{-1}AP=\Lambda = diag(\lambda_1,\lambda_2,\dots,\lambda_n)$ ：

注： $A^H中 i 需要变-i$ ,如： $\alpha = [1, 2, -i]^T$ ， $\alpha^H=[1,2,i]$