基于PEV的智能家居用电优化

一种考虑需求响应和隐私保护的智能家居用电优化调度方案

1. 引言

越来越多的电气设备接入电网，导致全社会用电量逐渐增加，用电峰谷差加大。此外，新能源也作为分布式电源接入电网，但由于受季节、气候等因素影响，新能源发电具有随机性、间歇性和发电不稳定的特点，给电网调度工作带来巨大挑战[1]。需求响应能够很好地应对可再生能源的不确定性[2,3]。高级量测体系（AMI）技术的细粒度电力采集为实施需求响应（DR）提供了技术支持[4]。在用电高峰时段，当电力供应不足时，电力系统可通过需求响应调节用户的用电负荷，实现削峰填谷、节能减排等目标，从而维持电网的稳定运行。文献’中提出了一种考虑用户主导的需求侧响应和点对点交易的智能社区能源管理方案，有助于能源共享并降低智能社区的能源账单[5]。用户主导的需求侧响应侧响应（UDDSR）与电池储能系统被引入到需求响应操作中，提高了用户负荷的利用效率。文献[6]中提出了一种分布式需求响应框架。在此方案中，用户根据独立系统运营商发布的价格信号调整其用电或发电模式。该方案同时最小化了供应商的发电成本和消费者的不适成本。文献[7]中提出了一种移动优化算法，以降低智能电网中的峰值用电，并减少用户的用电成本。文献[8]中提出了一种针对用户家庭中可调节负荷的基于激励的需求响应方案。该方案是一种新的需求响应方法，根据用户所承受的不便程度提供补偿。本杰明等人[9]采用约束非线性规划模型，通过削减高峰负荷、增加低谷负荷来优化居民用电消费，帮助电网运营商降低高峰时段的生产成本，并在低谷时段增加收入。该方案可利用基于激励的需求响应帮助居民用户从智能电网中获取更多收益。

在智能家居环境中，智能家居能源管理系统（SHEMS）通过智能电表（SMs）采集智能家居的实时细粒度用电信息，智能电表[10]将用电信息上传至电力控制中心（CC）。需求响应（DR）中央控制器（CC）发出的信号需要通过智能电表传输到家庭能源管理系统（SHEMS），SHEMS通过家庭局域网（HAN）实现电力调度，并合理安排用电。由于实时细粒度数据包含用户的详细用电信息，该过程可能导致用户隐私泄露[11]。为解决隐私泄露问题，研究人员开展了多项研究。一些研究提出了数据注入技术[12], ，即向智能电表数据中注入新数据以掩盖用户的用电数据。数据注入技术主要包括数据聚合技术和可充电电池技术。数据聚合技术[13]无法为单个用户提供增值服务，且方案计算成本较大，不适用于存储容量和计算能力有限的智能终端设备。可充电电池因安装成本低且隐私保护效果良好而受到青睐。徐等人[14]提出了一种包含太阳能发电和可充电电池的智能电表隐私保护方案，并分析了电池容量和太阳能发电对隐私保护的影响。但该方案采用太阳能发电成本较高。在[15],中采用负荷调度来保护用户隐私，通过随机化方法对隐私泄露、电费以及用户体验牺牲进行加权最小化，求解多目标优化问题。该方案在保证用户隐私的同时，降低了对电池容量的需求并减少了电池损耗。为克服因能源需求过高或过低而难以保障隐私的问题，穆罕默德等人[16]提出一种考虑时变目标输出负荷的启发式方法。该方案不仅能保护用户隐私，还能降低能源成本。为了减少对可充电电池的依赖，孙等人[17]结合电动汽车与空调系统替代可充电电池以保护用户隐私，并提出一种考虑用户需求随机性的马尔可夫决策过程，对方案性能进行评估。该方案可降低对电池的依赖并减少用户成本。杨等人[18]提出一种考虑隐私的家庭能源管理调度策略，利用可充电电池保护用户隐私，并引入偏好因子，使用户可在运行成本与隐私之间进行权衡。多米尼克等人[19]引入负荷隐藏技术，提出基于可控电池的负荷隐藏（BLH）和基于负荷的负荷隐藏（LLH），以模糊家庭用电需求，实验评估表明两种方案均可增强家庭隐私，且LLH可提升设备水平的隐私性。阿卜杜勒卡里姆等人[20]提出了两种隐私保护方案：单层消耗（OLC）可与需求响应管理结合使用。最大差值（MD）方法发送模糊的用电量值而非原始读数。本文方案引入了光伏、分布式电源和弹性负荷，不仅确保了收益最大化，也保障了隐私。上述所有方案均采用可充电电池来保护隐私，而本方案则使用插电式电动汽车（PEV）替代可充电电池。其优势如下：由于可充电电池的安装与维护需要一定成本，且混合需求响应资源的电动汽车正进入千家万户，因此本文采用PEV替代可充电电池，既节省了成本，又保证了用户的隐私。研究表明，家庭用插电式电动汽车平均有95%的时间处于在家闲置状态[21], ，这为本方案的实施奠定了基础。车辆到家庭（V2H）为PEV与智能家居之间的双向互动提供了技术支持，PEV可在电力系统处于低负载时通过充电桩利用低电价充电，并在电价高时为智能家居供电。PEV在外充电后回家为智能家居供电，这不仅可以从电价差中获利，还能避免智能家居的月用电量进入阶梯电价的高水平档位。此外，PEV还能保障用户隐私，隐藏实际功率，即实际用电功率低于智能电表检测到的功率。缺点是对于没有电动汽车的家庭，该方案可能不适用。

综上所述，本文的贡献如下：
1. 针对上述问题，提出了一种考虑需求响应和隐私保护的智能家居电力优化调度方案；
2. 给出了基于价格的需求响应(PDR)和基于激励的需求响应(IDR)下的智能家居电力负荷模型，在负荷建模中考虑了负荷功耗，并采用BAS算法获得最低用电成本，同时提出了一种彩票式IDR模型以鼓励用户参与需求响应；
3. 利用电动汽车储能来模糊用户的电力消耗数据，以保护用户隐私，并给出一种具有可调权重的隐私量化方法。仿真实验对比了三种不同调度策略下的用电成本以及该方案的隐私保护效果。

本文其余部分安排如下。第二部分介绍相关技术，如V2G和需求响应的详细内容，第三部分介绍智能家居的结构和功率负荷模型，第四部分建立了两种需求响应下的电力需求模型，第五部分给出了该方案的调度目标，并采用BAS算法进行求解，第六部分通过仿真实验比较了三种调度方案的性能以及插电式电动汽车储能对智能家居用电成本和隐私保护的效果，第七部分为本研究的总结。

2. 相关技术

2.1. 车辆到电网（V2G）技术

电动汽车的大规模普及以及无序充电可能会导致电力系统出现电压越限、线路过载和负荷波动等问题。然而，作为可控柔性负荷，电动汽车具有储能功能，并且能够向电网输送电能，从而实现电网与电动汽车之间的双向互动[22,23] 。即在负荷较低时，插电式电动车用户通过充电桩以低电价充电，在电价较高时为智能家居负荷供电，达到削峰填谷的目的。同时，插电式电动车用户可通过电价差获得收益，并降低智能家居的月总用电量，避免进入下一阶梯的高电价。

2.2. 需求响应

需求响应分为两种类型：基于价格的需求响应(PDR)和基于激励的需求响应(IDR)[24–26]。PDR通过建立分时电价引导用户转移功率负荷分布，是一种可控负荷调节方法；IDR由调度中心直接控制，引导用户参与系统备用服务，并支付相应的备用补偿。智能家居可以实时或近实时接收电价或IDR信号，根据该信号以及用户负荷的优先级，选择优化调度方案，在满足居民需求的同时降低家庭能源成本。’

2.3. 甲虫触角搜索算法

甲虫触角搜索算法（BAS算法）[27]是一种于2017年提出的高效智能优化算法。该算法具有计算量小、快速收敛、全局优化和代码简洁的优点。本文采用BAS算法求解目标函数的优化问题，得到最低耗电成本的最优调度策略。

3. 方案设计

3.1. 设计思路

为了缓解电网压力并实现负荷曲线的削峰填谷，需求响应和插电式电动车被广泛应用于智能电网中。本文提出了一种考虑需求响应和隐私保护的智能家居用电优化调度方案，该方案综合考虑了两种需求响应下的优化调度，以降低用户的功耗成本。此外，利用PEV储能电池为智能家居供电，可以模糊智能家居的用电模式，确保用户隐私，并降低用户的电力消耗成本。

3.2. 智能家居结构

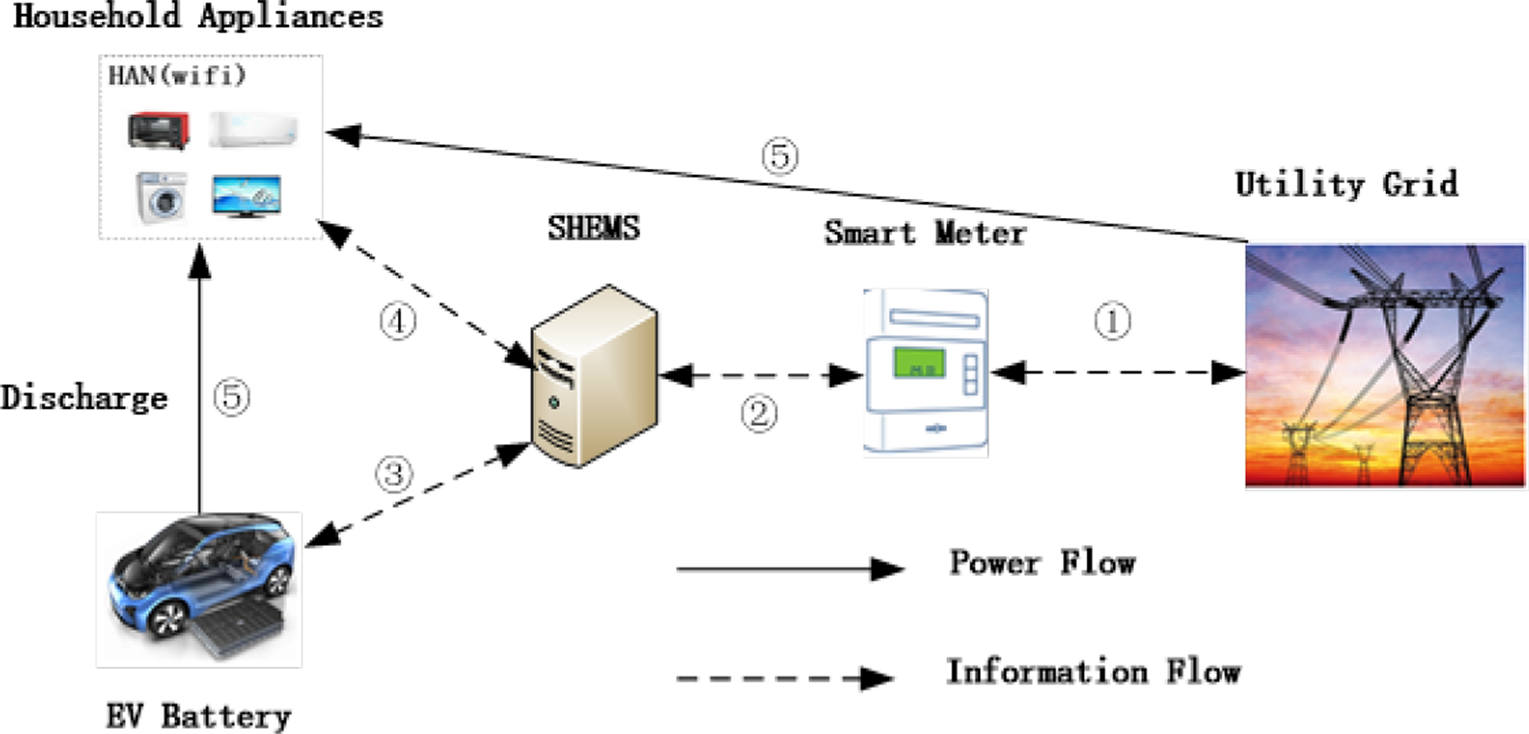
根据[28],中的智能家居架构图，构建了一个由家庭能源管理系统 SHEMS、插电式电动车PEV、家庭负荷、智能电表SM及其他实体组成的智能家居结构图，如图1所示。

各实体的功能如下：
SHEMS：家庭能源管理系统是实现智能家居能源调度的控制中心。一方面，SHEMS通过智能电表收集智能家居负荷的用电量信息，另一方面通过智能电表接收来自电网的需求响应信号，并通过家庭局域网合理安排智能家居负荷的用电计划，优先消纳PEV储能电池的电力，以最小化用户的用电量。

插电式电动车：除了削峰填谷以维持电网稳定外，电动汽车还可以在高峰时段向用户供电，使用户获得电价差收益。此外，PEV储能电池可为智能家居供电，模糊智能家居的用电模式，从而保护用户隐私。由于本方案中的插电式电动车不在智能家居内部充电，因此降低了智能家居的月用电量，避免进入高电价等级。

智能电表：智能电表收集智能家居中所有电力负荷的电力消耗信息，并将其发送给电力供应商。此外，智能电表还负责接收电力供应商发送的需求响应信号、电价信号、账单等信息。

3.3. 方案实施流程

1. 电力供应商发起激励型需求响应请求或调整某段时间的电价，并实时传输至智能电表。
2. 智能电表将接收到的信号传输至家庭能源管理系统。
3. 家庭能源管理系统制定最优调度策略，在峰时优先调度PEV储能电池为智能家居负荷供电。
4. 当PEV储能电池的能量耗尽后，家庭能源管理系统安排电网为智能家居供电。
5. 根据最优调度策略，PEV储能电池和电网同时或分别向智能家居供电。

4. 方案实现

4.1. 考虑需求响应的智能家居功率负荷模型

为了优化能源的使用，我们将智能家居用电负荷分为三类：不可延迟负荷、可延迟负荷和优先级负荷。需求响应模型旨在用户实施PDR或 IDR后建立家庭负荷计划，其中PDR主要通过需求弹性实现，IDR主要通过激励值或电价折扣实现。根据参考文献[29], ，PDR可以转移用户的负荷分布，但负荷削减能力不如IDR；IDR能够降低负荷峰值需求，但无法转移用户的负荷。因此，设计了一种包含两种需求响应和插电式电动车的智能家居功率负荷模型，并通过实验验证了该模型的性能。

4.1.1. 考虑需求响应的智能家居不可延迟负荷模型设计

在PDR和IDR下，构建了一天的电价弹性矩阵和每个用户的动态激励值，并获取了智能家居在最大效益下的电力需求，作为响应负荷。

（1）PDR模型设计
价格型需求响应主要通过需求弹性实现，弹性系数[30]表达如下：

$$
e_{t,t} = \frac{\Delta P^{DR} t}{\Delta \rho^{DR}_t} \cdot \frac{\rho^0_t}{P^0_t}, \quad e {t,t} \leq 0 \tag{1}
$$

其中，$e_{t,t}$表示自弹性系数，用于描述在时间段t内用电量变化与电价变化之间的关系。$\Delta P^{DR}_t$表示需求响应后电力的变化，$\Delta \rho^{DR}_t$表示电价的变化，$\rho^0_t$而 $P^0_t$表示需求响应前的电价和电力消耗。价格弹性矩阵如下：

$$
e = \begin{bmatrix}
e_{1,1} & \cdots & e_{1,T} \
\vdots & \ddots & \vdots \
e_{T,1} & \cdots & e_{T,T}
\end{bmatrix} \tag{2}
$$

(2) 彩票式IDR模型设计
为了维持电网稳定性并减少高峰时段的用电量，电力公司向用户发放激励值以鼓励其参与激励型需求响应（IDR）。但激励值的设定是一个关键问题：激励值过小会导致用户参与度低；激励值过大则会降低电网收益。通常情况下，用户不会因奖励过少而在中午关闭空调。因此，为了增强用户粘性，本文提出了一种高奖池机制，即用户参与需求响应的程度越高，其中奖概率越大，获得的奖励也越多。我们定义中奖概率 ε如下：

$$
\varepsilon = x_i \cdot p_{initial}, \quad \varepsilon \in [0, 1) \tag{3}
$$

其中，$x_i$表示用户i参与需求响应的次数。$p_{initial}$表示电力公司设定的初始中奖概率。

$$
B_t = \begin{cases}
B, & \varepsilon = x_i \cdot p_{initial} \
B_t, & \varepsilon = 1 - x_i \cdot p_{initial}
\end{cases} \tag{4}
$$

其中，$B$ 表示电力公司设定的高激励值，$B_t$表示用户在时间t获得的实际激励值（未中奖时的低激励值）。

（3）考虑PDR和IDR的智能家居不可延迟负荷模型设计
总之，用户参与需求响应的收益是：

$$
V(P^{DR} t) = U(P^0_t) + \rho^0_t \cdot (P^{DR}_t - P^0_t) \cdot \left(1 + \frac{P^{DR}_t - P^0_t}{2e {t,t} \cdot P^0_t}\right) - \rho^{DR}_t \cdot P^{DR}_t + B_t (P^0_t - P^{DR}_t) \tag{5}
$$

其中$U(P^0_t)$表示用户在时刻t用电量为$P^0_t$时的收益，$P^{DR} t$表示用户执行需求响应后的用电量，$\rho^{DR}_t$表示时刻t的需求响应下的实时电价。根据参考文献[31,32],当$\partial V(P^{DR}_t)/\partial P^{DR}_t = 0$时，用户获得最大收益。$P^t {UN}$表示时刻t不可延迟负荷的总功率。对公式(5)进行推导后，用户在时刻t执行需求响应调整后的负荷需求为：

$$
P^{DR} {t,URN} = P^t {UN} \cdot \left(1 + e_{t,t} \frac{\rho^{DR}_t - \rho^0_t + B_t}{\rho^0_t}\right) \tag{6}
$$

4.1.2 考虑需求响应的智能家居可延迟负荷设计

可延迟负荷没有固定的使用时间，且仅需在给定时间范围内完成任务，用户只关心任务结果。可延迟负荷具有较大的调度灵活性，是家庭能源管理系统（SHEMS）的主要调度优化对象。通过SHEMS的优化调度，可延迟负荷可以帮助用户缓解高峰电力消耗并降低用户的用电成本。

（1）考虑PDR和IDR的智能家居可延缓负荷设计
将一天划分为T个时段，L表示智能家居中可延缓负荷的数量。$P_{avg}$表示负荷的平均功率。二进制变量$S^t_L$表示负荷l的状态，$S^t_L = 1$表示负荷开启；$S^t_L = 0$表示负荷关闭。时间t智能家居中负荷L的总电力消耗如下所示。

$$
P^t_{DE} = \sum_{L}^{l=1} S^t_L \cdot (P_{avg})_l \tag{7}
$$

计算可交叉弹性系数 $e_{t,s}$，类似于不可延迟负荷：

$$
e_{t,s} = \frac{\Delta P^{DR} t}{\Delta \rho^{DR}_s} \cdot \frac{\rho^0_s}{P^0_t}, \quad e {t,s} \geq 0 \tag{8}
$$

其中，$\rho^0_s$ 表示在时段 $s$ 需求响应前的电价，$\Delta \rho^{DR}_s$ 表示在时段 $s$ 需求响应后电价的变化量。

类似地，计算需求响应后可延迟负荷的负荷需求为：

$$
P^{DR} {t,DE} = P^t {DE} \cdot \left(1 + \sum_{s=1}^{T} e_{t,s} \frac{\rho^{DR}_s - \rho^0_s + B_s}{\rho^0_s}\right) \tag{9}
$$

(2) 不可中断负荷模型设计

可延迟负荷可进一步细分为可中断负荷和不可中断负荷。不可中断负荷从设备启动到任务完成必须保持连续工作时间，此类负荷包括洗衣机、洗碗机等。不可中断负荷模型如下：$T_l$表示完成负载l，$[t_b, t_e]$表示允许负荷运行的时间范围，二进制变量$S^t_{NL}$表示不可中断负荷的状态，$t_s$表示负荷开启的时刻。负载l的运行时间约束如下所示。

$$
\sum_{t=t_b}^{t_e} S^t_{NL} = T_l \tag{10}
$$

$$
S^t_{NL} \in {0, 1} \tag{11}
$$

如公式(10)所示，不可中断负荷只需在时间范围$[t_b, t_e]$内选择一段连续的时间完成任务，其持续时间为$T_l$。

(3) 可中断负荷模型设计

可中断负荷的工作时间是离散的，用户对其工作不具有实时性和连续性要求。这类负荷可在允许工作的时间段内随时启动或停止工作。因此，此类负荷是可中断负荷中最重要的调度对象。通过家庭能源管理系统（SHEMS）的优化调度，可以降低具有碎片化运行时间用户的功率压力。此类负荷包括电动汽车、空调等。可中断负荷模型如下：

$$
S^t_{IL} = {0, 1}, \quad t \in [t_b, t_e] \tag{12}
$$

在智能家居负荷中，存在一些具有时间协同的设备，它们属于多任务工作模式。例如，烘干机需要在洗衣机之后运行。这种多任务可中断负荷建模如下： $r \in {1, 2, 3, \cdots, R}$ 表示一个任务集，$S_{IL}(r, t)$ 表示在时间 $t$, $T_r$ 时任务 $r$的负荷工作状态，$[t_b, t_e]$ 表示多任务工作的时长范围。

$$
S_{IL}(r, t) = {0, 1}, \quad t \in [t_b, t_e] \tag{13}
$$

$$
\sum_{t=t_b}^{t_e} S_{IL}(r, t) = T_r, \quad r \in {1, 2, 3, \cdots, R} \tag{14}
$$

为了确保多任务的时间顺序，在任务r开始之前，前 $r - 1$个任务必须已完成，约束条件如下。

$$
\sum_{r’=1}^{r-1} \sum_{t=t_b}^{t_e} S_{IL}(r’, t) \geq \sum_{r’=1}^{r-1} T_{r’} \cdot S_{IL}(r, t) \tag{15}
$$

根据用户的意愿，任何家庭负荷都可以被分类为优先级负荷。对于被归类为优先级负荷的设备，家庭能源管理系统将优先调度电力以确保其稳定运行；对于未被列为优先级负荷的设备，家庭能源管理系统则根据设备自身的特性安排电力调度。

4.1.3 需求响应下的电动汽车负荷模型设计

考虑需求响应的能源存储如下：

$$
P^t_{grid} = P^t_{DR} - P^t_{pev}, \quad t = 0, 1, \cdots, T - 1 \tag{16}
$$

$$
P_{min} \leq P^t_{pev} \leq P_{max} \tag{17}
$$

$$
S^t_{pev} = \begin{cases}
0, & \text{Discharge} \
1, & \text{Charge}
\end{cases} \tag{18}
$$

其中，$P^t_{pev}$表示电动汽车的功率，$P^t_{DR}$表示智能家居执行需求响应后的负荷总功率，$P^t_{grid}$表示需要从电网获取的功率。$P_{min}$和$P_{max}$分别表示电动汽车的最小功率和最大功率。二进制变量$S^t_{pev} = 0$表示电动汽车处于放电状态，$S^t_{pev} = 1$表示电动汽车处于充电状态。为了确保用户的最大效益，我们让电动汽车在低电价时通过充电桩充电，在用电高峰期向智能家居供电。电动汽车不在智能家居内充电，以避免用户月用电量过高，并防止电荷进入下一阶梯。考虑需求响应的电动汽车充电模型如下：

时间t内电动汽车充满电所需的电荷：

$$
H_t = \sum_{t} P_{pev} \cdot y_t \cdot h_t \tag{19}
$$

其中$P_{pev}$表示电动汽车的功率，$h_t$表示电动汽车的充电时间，$y_t$表示时间t的电价。

对于电动汽车用户，价格变化和激励值可以引导用户改变充电行为。需求响应后，时刻t的负荷$D^{DR}_{t,pev}$以及电动汽车数量$A^{DR}_t$分别如下：

$$
D^{DR} {t,pev} = D^0 {t,pev} \cdot \left(1 + \sum_{s=1}^{T} e_{s,t} \cdot \frac{H_s - H_t + B^{pev}_s}{H_s}\right) \tag{20}
$$

$$
A^{DR} t = \sum {s=1}^{T} \left( e_{s,t} \cdot \frac{H_s - H_t + B^{pev}_s}{H_s} \cdot A^0_t \right) \tag{21}
$$

其中$A^0_t$表示需求响应前t时间内充电的电动汽车数量，$B^{pev}_s$ 表示激励值。

插电式电动汽车不仅作为日常交通工具，还充当智能家居中的储能载体。因此，插电式电动车可以缓解家庭在高峰时段的压力，同时还能削峰填谷以维持电力系统的稳定性。与此同时，插电式电动车需满足以下约束：PEV可行驶距离、PEV的充放电功率、PEV储能电池的可用容量以及PEV的充电价格。其约束模型如下：

（1）PEV可行驶距离

$$
M_{max} = \begin{cases}
(E_{out} - E_{in}) \cdot M_{avg}, & E_{in} > E_{min} \
(E_{out} - E_{min}) \cdot M_{avg}, & E_{in} < E_{min}
\end{cases} \tag{22}
$$

其中$E_{in}$ 和$E_{out}$ 分别表示电动汽车通电和断电时的存储能量。$E_{min}$是电动汽车功率的临界值，起到保护电动汽车的作用。$M_{avg}$ 表示单位电动汽车可行驶的距离。

(2) PEV的充放电功率

$$
0 \leq P^t_{ch} \leq S^t_{pev} \cdot P^{max}_{ch} \tag{23}
$$

$$
0 \leq P^t_{dish} \leq (1 - S^t_{pev}) \cdot P^{max}_{dish} \tag{24}
$$

其中，$P^t_{ch}$ 和$P^t_{dish}$ 分别表示PEV的充放电功率，$P^{max} {ch}$ 和$P^{max} {dish}$ 分别表示 PEV充放电功率的最大值。为了保护PEV储能电池，规定不能同时进行充放电，则：

$$
P^t_{ch} \cdot P^t_{dish} = 0 \tag{25}
$$

4.2. 智能家居用电负荷隐私量化模型

为了量化隐私保护的效果，参考文献[18]引入了决策系数R²，R² = 1表示智能电表记录的电力消耗与实际家庭负荷完全相同，R² = 0表示智能电表记录的电力消耗与实际总电力消耗不同。即，R²越接近零，隐私保护效果越好。

$$
R^2 = 1 - \frac{\sum_{t=1}^{T} (P^t_{\text{meter}} - P^t_{\text{load}})^2}{\sum_{t=1}^{T}( P^t_{\text{meter}} - \bar{P} {\text{meter}})^2 + \sum {t=1}^{T} (P^t_{\text{meter}} - P^t_{\text{load}})^2} \tag{28}
$$

其中，$P^t_{\text{load}}$ 表示智能家居中所有负荷的总电力消耗，$\bar{P}_{\text{meter}}$表示智能电表测得的平均值。

5. 方案调度目标

5.1. 考虑需求响应和隐私保护的最优调度目标

家庭能源管理系统的调度目标是在尽可能满足用户需求的同时，节省用户的用电成本。也就是说，SHEMS应在需求响应条件下合理安排家庭负荷的工作，并在用电高峰时段合理分配插电式电动车的能源，使家庭负荷从大电网购电的数量最少，从而确保用户成本最低。此外，在考虑隐私保护时，上述单目标优化问题被转化为多目标优化问题。通过引入偏好因子 α，将其转化为如下所示的单目标优化模型[18]：

$$
\min F = \alpha \left{ \sum_{t=1}^{T} \left[ \rho_t (P^{DR} t - P^t {\text{batt}}) - B_t \Delta P_t \right] + \sum_{s=1}^{T} P^{DR} {s,\text{pev}} \cdot \rho_s + C {\text{pev}} \right} + (1 - \alpha)\beta \sum_{t=1}^{T} (P^{t+1} {\text{meter}} - P^t {\text{meter}})^2 \tag{29}
$$

$$
P^t_{\text{meter}} = P^t_{DE} + P^t_{UN} - P^t_{\text{pev}} \tag{30}
$$

$$
P^t_{\text{batt}} = P^t_{\text{ch}} - P^t_{\text{dish}} \tag{31}
$$

其中$P^t_{\text{meter}}$表示智能电表检测的总电力消耗。$\alpha \in (0,1)$由用户设定，用于衡量电费与隐私之间的权衡，$\beta$是用于计算单位货币隐私泄露的常数。$C_{\text{pev}}$表示电动乘用车的成本，$\Delta P_t$表示需求响应后智能家居的负荷变化，$P^{DR}_{s,\text{pev}}$表示充电桩中插电式电动车的充电容量。

公式(29) 受约束于 公式(1–28)，并且仍然是约束的：

$$
\begin{cases}
\Delta P_t \geq 0 \
\Delta P_{\text{pev}} \geq 0 \
\rho_s \leq \rho_t
\end{cases} \tag{32}
$$

5.2. 基于BAS算法的电力最优调度方案求解

5.2.1. BAS算法模型

1. 变量步长因子

$$
\text{step}(t) = \text{step}(t - 1) \cdot \text{eta} + \text{step}(0), \quad \text{eta} \in [0, 1] \tag{33}
$$

$$
\text{step}(t) = c \cdot d(t) \tag{34}
$$

其中，$t$ 表示迭代次数，$\text{step}(t)$ 表示第 $t$ 次的步长，$\text{eta}$ 和 $c$ 由用户定义，$c$ 为固定常数，通常取值小于 $\text{eta}= 0.95$。$d(t)$ 表示甲虫左右触须之间的距离。初始步长$\text{step}(0)$ 一般设置为较大的值，最好等于自变量的最大长度，以确保能够覆盖整个区域。

2. 随机方向向量

$$
\begin{cases}
\text{dir} = \text{rands}(n, 1) \
\text{dir} = \text{dir}/\text{norm}(\text{dir})
\end{cases} \tag{35}
$$

其中，$n$ 表示空间维度，$\text{norm}()$ 表示归一化函数。

3. 左右天线的空间坐标

$$
\begin{cases}
x_l(t) = x(t) + d(t) \cdot \text{dir}/2 \
x_r(t) = x(t) - d(t) \cdot \text{dir}/2
\end{cases} \tag{36}
$$

其中$x_l$表示左触角坐标，$x_r$表示右触角坐标，$x$表示质心坐标，$d$ 表示两天线之间的间距。

4. 适应度值

$$
\begin{cases}
f_{\text{left}} = f(x_l) \
f_{\text{right}} = f(x_r)
\end{cases} \tag{37}
$$

5. 下一个位置

$$
x(t) = x(t - 1) - \text{step}(t) \cdot \text{dir} \cdot \text{sign}(f_{\text{left}} - f_{\text{right}}) \tag{38}
$$

其中$\text{sign}()$表示符号函数。

5.2.2. 算法设计

上述目标函数的目标是在保护用户隐私的同时，尽可能降低用户的功耗成本。用户需要权衡功耗成本与隐私保护，并自行设置α的值以满足自身需求。我们将上述目标函数的功率问题转化为数学问题。利用BAS算法，我们设计了以下算法来求解该目标函数的优化问题。

函数，然后获得最优调度策略。

公式(29)中的目标函数旨在让用户通过设置α的值来平衡成本和隐私，α是一个常数，由用户设定。因此，无论用户的隐私要求多高，都必须确保当前用电量最低。基于此，我们给出目标函数：

$$
\min F_P = \sum_{t=1}^{T} \left[ \rho_t (P^{DR} {t,URN} + P^{DR} {t,DRE} \cdot S^t_L - P^t_{\text{batt}}) - B_t \Delta P_t \right] + \sum_{s=1}^{T} P^{DR} {s,\text{pev}} \cdot \rho_s + C {\text{pev}} \tag{39}
$$

模型中有两种变量：连续型和0–1离散型，它们受到插电式电动汽车储能和需求响应的约束。这是一个具有可变参数的非线性多目标优化问题[33]，求解解集较为困难。因此，本文选用BAS算法来求解该解集。与粒子群优化算法相比，BAS算法仅需一个个体，而粒子群优化算法需要整个种群共同寻优，从而大大降低了计算成本。利用BAS算法求解甲虫在每一点的最优值，甲虫的最终路径即为最优电力调度策略。

（1） 变量编码
假设有m个可延迟负荷，每个可延迟负荷i有n个任务，二进制变量$S^t_L$和连续变量$P^{DR}_{s,\text{pev}}$在最优调度区间$t \in [1, 24]$内进行编码，则：

$$
P^{i,DR} {\text{pev}} = (P^{i,DR} {1,\text{pev}}, P^{i,DR}_{24,\text{pev}}) \tag{40}
$$

$$
S_{i,j} = (S^1_{i,j}, S^2_{i,j}, \cdots, S^{24}_{i,j}) \in {0, 1}^{24} \tag{41}
$$

因此，总控制量编码为 $X_i = (S_{i,1}, \cdots, S_{i,j}, \cdots, S_{i,n}, P^{i,DR}_{\text{pev}})$，且每个$X_i$是一种针对智能家居用电的优化调度方案。

（2） 位置更新
根据公式(38)更新下一个位置。

（3） 算法步骤
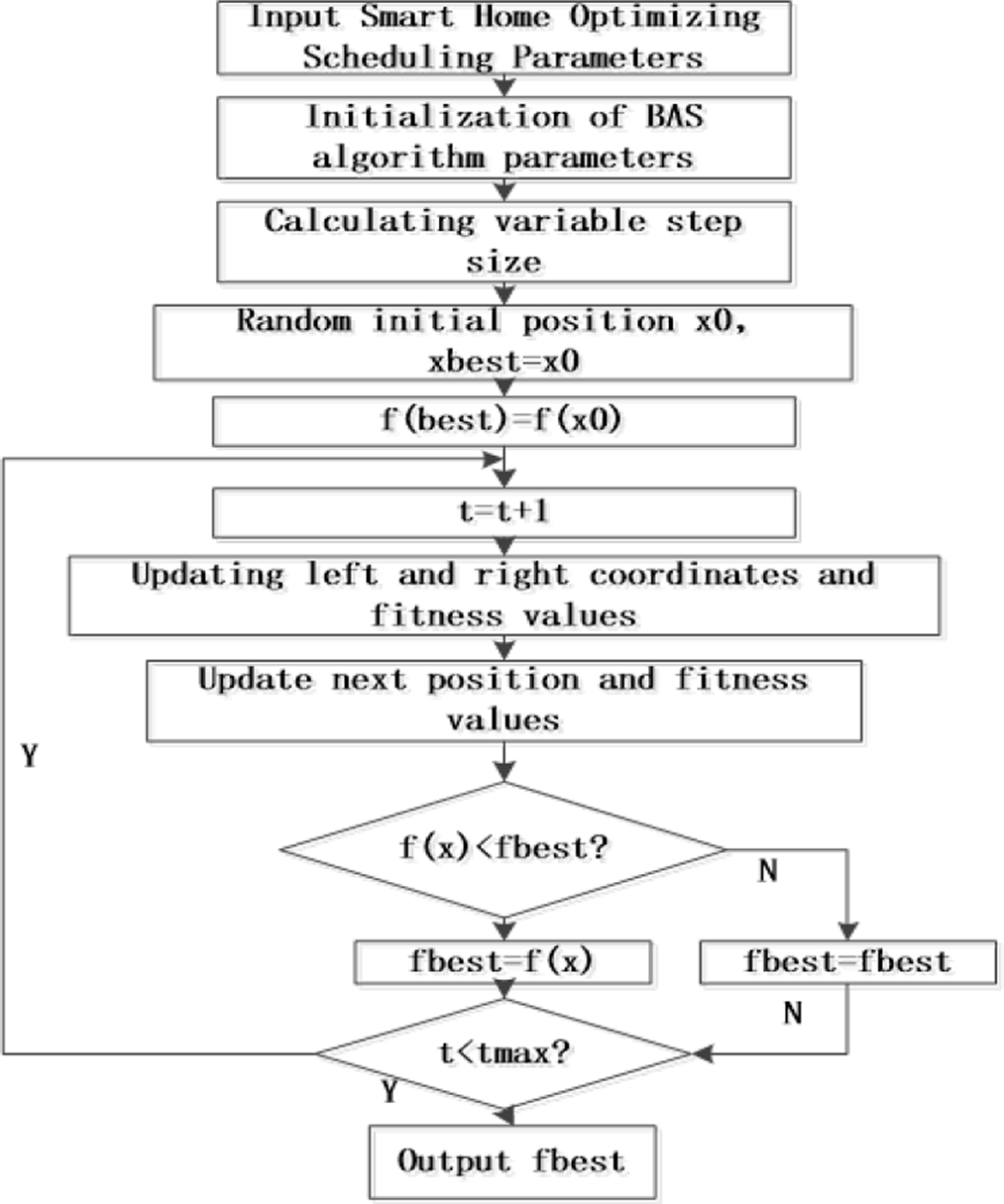
BAS算法的流程图如图2所示：

1. 参数初始化。用户输入 α和 β，SHEMS获取智能家居的电力消耗数据和需求响应激励值。初始化BAS算法参数 eta、c、t= 0以及最大迭代次数 tmax。步长因子通过公式(33)(34)计算。
2. 随机给定甲虫的初始位置 x₀，令 x_best = x₀, 计算适应度，并将值赋给 f_best, f_best = f(x_best) = f(x₀)。
3. 计数器 t = t + 1，通过公式(36)更新左右触角坐标，并通过公式(37)计算左右触角的适应度值。比较左右触角的适应度值后，通过公式(38)更新下一个位置，并计算当前适应度值 f(x_t)。
4. 比较当前值 f(x_t) 和 f_best，如果 f(x_t) < f_best，则 f_best = f(x_t)。
5. 比较 t 和 t_max，如果 t = t_max，则进入第六步；否则返回第三步。
6. 结束算法，输出最优解f_best，即智能家居的最低用电成本。

6. 仿真实验与结果分析

6.1. 仿真参数设置

采用上述模型和BAS算法，以夏季某智能家居的电力消耗情况为例，在MATLAB环境中进行仿真，相关仿真参数设置如表1所示。目前，中国采用分时电价来维持电网的稳定。根据文献[34]，时段划分及交易价格如表2所示，表中还给出了不同负荷条件下高峰时段的价格弹性系数和激励值。如文献[18]所述，表3展示了夏季智能家居中可移动负荷全天的运行时间和电力消耗，其中洗碗机、洗衣机和电饭煲为不可中断负荷。

参数说明	符号	值	Unit
总持续时间	T	24	hour
时间步长	t	1	hour
PEV充电时段	t_ch	0:00~8:00	hour
PEV放电时段	t_dish	12:00~14:00, 17:00~23:00	hour
最大电池能量	E_max	26.5	kWh
最小电池能量	E_min	4	kWh
日间行驶能量	E_dr	3.4	kWh
PEV功率	P_pev	3	kW

表1 仿真参数表

Load时间段	购电价格（元/千瓦时）	售电价格（元/千瓦时）	激励价格（元/千瓦时）	弹性系数
Peak	Flat	谷时
Peak 11:00~14:00	0.84	0.75	0.1326	-0.02 0.0032 0.0024
18:00~23:00
Flat 8:00~10:00	0.61	0.57	0	0.0032 -0.02 0.002
15:00~17:00
谷时 00:00~7:00	0.31	0.27	0	0.0024 0.002 -0.02

表2 分时电价和价格弹性系数表

Load	[tb，te]	持续时间 (h)	功率 (kW)	用户需求
洗碗机	8:00~12:00	1	0.73	不可中断 20:00~23:00
电饭煲	6:00~7:30	1	0.8	不可中断 15:00~17:00
洗衣机	6:00~9:30	2	0.38	不可中断 18:00~20:30
加湿器	0:00~9:00	4	0.15	45%~65%RH 14:00~20:30
洗衣干燥机	9:00~12:00	1.5	1.26	洗衣后 机器 20:00~23:00
热水器	4:00~8:30	2	1.85	42~55 16:00~20:00 21:00~24:00
电水壶	6:00~7:30	0.5	1.5	80~95 20:00~23:00
电烤箱	9:00~12:30	1	1.3	100~250 15:00~17:00 19:00~22:00
Air conditioner	11:00~15:00	4	2.2	23~26 17:00~23:00

表3 智能家居可移动负荷参数表

6.2. 智能家居三种优化调度策略的仿真

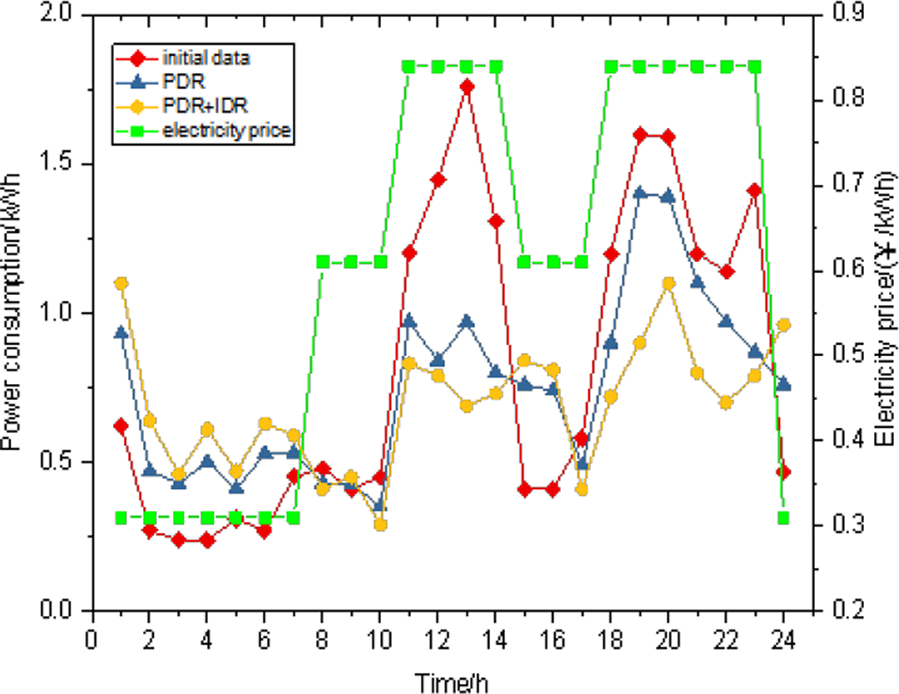
智能家居能源管理系统（SHEMS）的优化调度方案主要基于分时电价进行用户的负荷转移，旨在最小化用户的用电成本。通过转移用户负荷分布来降低用电成本的方法，可视为用户对价格型需求响应（PDR）请求的响应。我们将价格型需求响应（PDR）与激励型需求响应（IDR）相结合，比较在不参与需求响应、仅参与PDR以及同时参与两种需求响应三种情况下，智能家居一天内的负荷需求，如图3所示。

分析图3表明，结合两种需求响应的调度方案具有最佳的优化效果。该方案每天最多可将峰时用电减少1.07千瓦时。用户在无需求响应情况下的日用电成本为14.2035，采用价格型需求响应时成本为11.942，而在两种需求响应下的用电成本模式为10.4127。在扣除激励值后，该方案的日用电成本相比无需求响应的方案可降低29.26%，相比价格型需求响应方案可降低15.86%。该方案不仅能削峰填谷，还能转移用户的用电需求，保障电网稳定性并降低用户的用电成本。

6.3. 插电式电动车充电对智能家居用电成本的影响

(1) 使用插电式电动汽车储能模拟用户的用电成本。
作为移动电源的载体，PEV储能电池不仅为人们的出行提供了便利，还为用户节省了用电成本。PEV的直流电通过逆变器转换为交流电功率转换系统（PCS）以及V2H系统可从插电式电动车的电池中转换6千瓦的功率。例如，比亚迪已在其大多数新能源汽车上增加了移动电站功能。通过特制的适配器电缆，电池的电力可以以220伏电压供给家用电器。

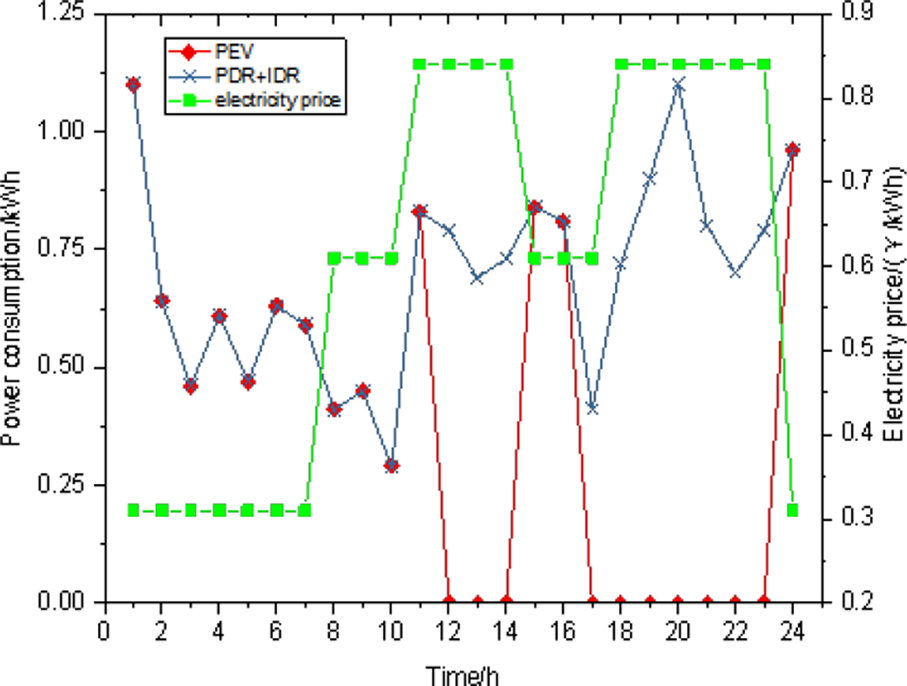
根据上述仿真参数，给出了由PEV储能电池供电的智能家居的日功率需求，如图4所示。

分析图4表明，采用PEV储能电池供电的家庭用电量大幅减少，与两种未使用插电式电动车方法的需求响应相比，用电成本降低了56.33%。然而，仍需考虑PEV储能电池的成本以及插电式电动车的充电成本。假设插电式电动车每天充电6小时，每次充电可供用户约两天的出行和家用。每日总功率成本降低了28.56%。

(2) 插电式电动车充电模式对用户用电成本的影响。
我们设定了插电式电动车的充放电时段，并确保插电式电动车仅在如车库或室外的充电桩进行充电，这样除了赚取差价外，用户还能确保每月用电量较小，避免进入下一阶梯电价。表4展示了夏季不同阶梯居民电价表。

我们考虑插电式电动车在智能家居中充电和在充电桩充电两种情况，并分别计算当前月份智能家居用户在这两种情况下的用电量。电力消耗如图5所示。

当使用阶梯电价计算用户的电费时，由于存在峰时和谷时电价，需要先按分时电价再按阶梯电价进行计算。根据表4中的数据，按每月30天计算，在家充电和在充电点充电的插电式电动车充电时间和电价相同。在家充电时，插电式电动车被视为家用电器，智能家居的用电需求如表5所示。

User 类别	分级功率（kWh/一次*m)	电价（/kWh）
阶梯电价 user	第一档 0~260	0.68
	第二档 261~600	0.73
	第三档水平 >601	0.98

表4 夏季不同阶梯居民电价表

方法	家庭负荷(kWh)	PEV负荷(kWh)	每月家庭负荷(kWh)
	Peak	Flat	谷时
充电在 home	0.83	2.8	23.46
充电在外	0.83	2.8	5.46

表5 两种充电模式下智能家居的电力负荷需求。

分析表4和表5显示，在家充电的插电式电动车月用电量已达到第三阶梯电价，而在外充电的PEV月用电量已达到第二阶梯电价。根据表5中的计算，在家充电的月电费为371.144，而在外充电的月电费为290.969，比在家充电低21.6%。

6.4. 考虑隐私的智能家居优化调度仿真

根据第4.2节中的隐私量化方法，仿真显示当α取不同值时，智能电表的测量功率如图6所示。

分析图6表明，利用插电式电动汽车储能电池可以确保智能家居的隐私，使智能电表读数变化不大。且α的值越大，智能电表数据越平滑，即隐私保护效果越好，但用户的用电量也越高。换句话说，用户需要权衡用电成本与隐私保护，设置α的值以满足自身需求。

7. 结论与展望

为了维持电力系统的稳定性以及智能家居的低成本和隐私性，提出了一种考虑需求响应和隐私保护的智能家居用电优化调度方案。本方案利用PDR和IDR实现智能家居用电的优化调度。引入PEV储能电池以降低用户的用电成本，同时确保用户的用电隐私。仿真结果表明，与传统调度方案相比，该方案的电力消耗更少，且用户可通过设置α的值来平衡功耗成本与隐私之间的关系。本方案未考虑电动汽车可充电电池的损耗问题，这将是我们的后续工作。