机器学习中的偏差(bias)和方差(variance)

版权声明：本文为博主原创文章，未经博主允许不得转载。 http://blog.csdn.net/mingtian715/article/details/53789487

内容参见stanford课程《机器学习》

对于已建立的某一机器学习模型来说，不论是对训练数据欠拟合或是过拟合都不是我们想要的，因此应该有一种合理的诊断方法。

偏差和方差

评价数据拟合程度好坏，通常用代价函数J（平方差函数）。如果只关注Jtrain(训练集误差)的话，通常会导致过拟合，因此还需要关注Jcv(交叉验证集误差)。

高偏差：Jtrain和Jcv都很大，并且Jtrain≈Jcv。对应欠拟合。

高方差：Jtrain较小，Jcv远大于Jtrain。对应过拟合。

下图d代表多项式拟合的阶数，d越高，拟合函数越复杂，越可能发生过拟合。

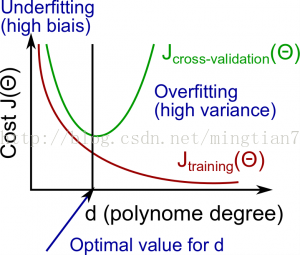
如何理解高偏差和高方差

1、高偏差对应着欠拟合，此时Jtrain也较大，可以理解为对任何新数据（不论其是否属于训练集），都有着较大的Jcv误差，偏离真实预测较大。

2、高方差对应着过拟合，此时Jtrain很小，对于新数据来说，如果其属性与训练集类似，它的Jcv就会小些，如果属性与训练集不同，Jcv就会很大，因此有一个比较大的波动，因此说是高方差。

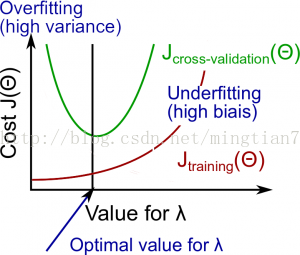
实际优化过程中，更多的是调整防止过拟合 参数λ，λ 对应正则化系数（越大，对过拟合的限制越强）。下图为λ和Jtrain、Jcv理想曲线。

学习曲线

学习曲线是描述Jtrain和Jcv和数据样本规模的关系曲线。参见下图

                                     

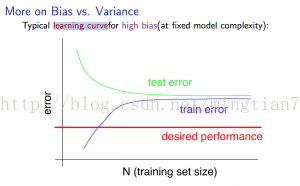
左图对应高偏差（欠拟合），右图对应过拟合。可以看出当模型属于高偏差时，随着样本数据规模增大，性能不会有什么改善，过拟合中的误差则在持续减小。这个很好理解，欠拟合一般是模型比较简单，不能准确的描述数据特征，因此盲目增大数据量是没用的；而过拟合是模型比较复杂，描述数据过于准确了，因此增加一些数据量可以减小过拟合。

模型修改策略

过拟合：增大数据规模、减小数据特征数（维数）、增大正则化系数λ

欠拟合：增多数据特征数、添加高次多项式特征、减小正则化系数λ

实际优化过程中，我们的目标就是使模型处于欠拟合和过拟合之间一个平衡的位置。