【动手学习深度学习】概率+代码实现

简单来说，机器学习就是做出预测。

#导包
%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l

fair_probs = torch.ones([6])/6
multinomial.Multinomial(1,fair_probs).sample()

tensor([0., 1., 0., 0., 0., 0.])

multinomial.Multinomial(10,fair_probs).sample()

tensor([1., 0., 3., 2., 1., 3.])

#模拟1000次投掷
#将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000,fair_probs).sample()
counts / 1000 #相对频率作为估计值

tensor([0.1670, 0.1730, 0.1590, 0.1630, 0.1700, 0.1680])

#概率如何随着时间的推移收敛到真实概率
counts = multinomial.Multinomial(10,fair_probs).sample((500,)) #进行500组实验，每组抽取10个样本
cum_counts = counts.cumsum(dim=0) #按行累加
estimates = cum_counts / cum_counts.sum(dim=1,keepdims=True) #计算频率

d2l.set_figsize((6,4.5))
for i in range(6):
    d2l.plt.plot(estimates[:,i].numpy(),
                label=("P(die="+str(i+1)+")"))
d2l.plt.axhline(y=0.167,color='black',linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend()
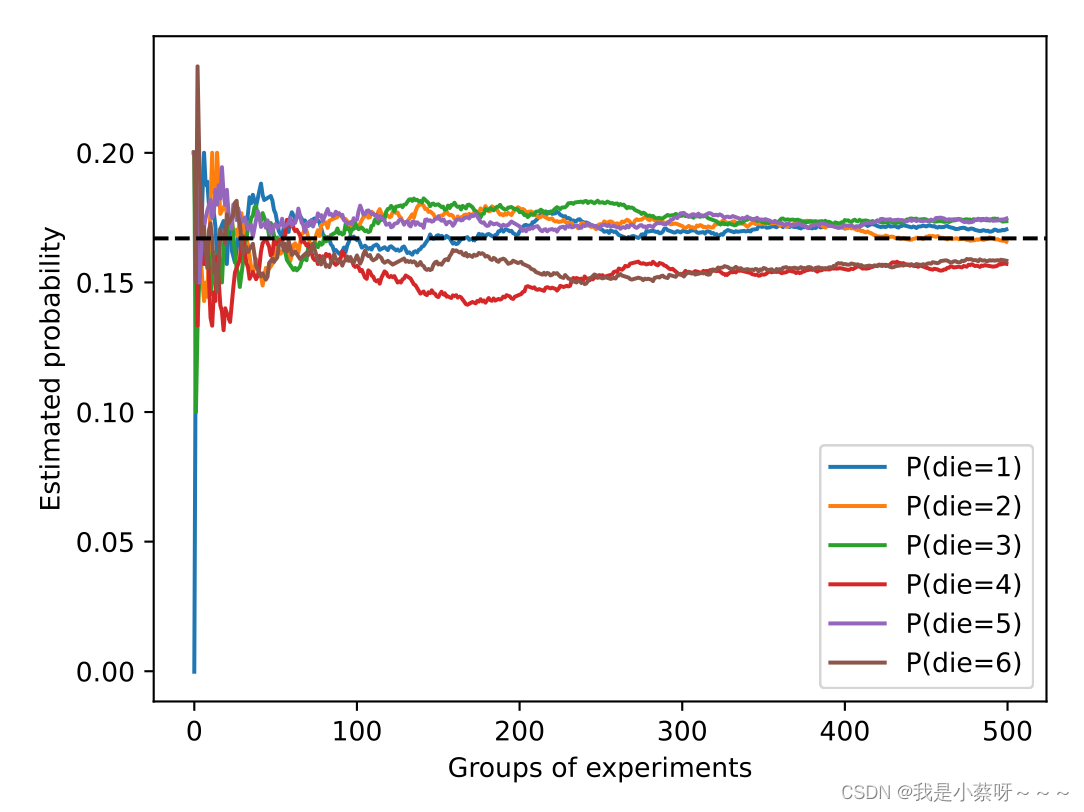
#每条实线对应于骰⼦的6个值中的⼀个，并给出骰⼦在每组实验后出现值的估计概率。
#当我们通过更多的实验获得更多的数据时，这6条实体曲线向真实概率收敛。