8.1 线性变换的思想

一、线性变换的概念

当一个矩阵 $A$ 乘一个向量 $\mathbf{v}$ 时，它将 $\mathbf{v}$ “变换” 成另一个向量 $A\mathbf{v}$. 输入 $\mathbf{v}$，输出 $T(\mathbf{v})=A\mathbf{v}$. 变换 $T$ 和函数类似：对于函数，输入数字 $x$，输出 $f(x)$；对于变换，输入一个向量 $\mathbf{v}$，我们用矩阵左乘这个向量，输出 $T(\mathbf{v})$. 我们更深入的目标是所有向量 $\mathbf{v}$ 的变换，当我们用矩阵 $A$ 左乘每个向量 $\mathbf{v}$ 时，我们是在变换整个空间 $V$.
先从矩阵 $A$ 开始，它将 $\mathbf{v}$ 变换成 $A\mathbf{v}$，将 $\mathbf{w}$ 变换成 $A\mathbf{w}$，当 $\mathbf{u}=\mathbf{v}+\mathbf{w}$ 时，我们得到 $A\mathbf{u}$ 等于 $A\mathbf{v}+A\mathbf{w}$. 矩阵乘法 $T(\mathbf{v})=A\mathbf{v}$ 给出了一个线性变换（linear transformation）：

$$\begin{gathered} 一个变换T对于每个输入的向量\mathbf{v}都对应一个输出T(\mathbf{v}). \\ 如果对于所有的\mathbf{v}和\mathbf{w}都满足如下条件，则这个变换是线性的： \\ (a)T(\mathbf{v}+\mathbf{w})=T(\mathbf{v})+T(\mathbf{w})(b)对于任意的c都有:T(c\mathbf{v})=cT(\mathbf{v}) \end{gathered}$$

由上述定义可知，如果输入 $\mathbf{v}=0$，则输出一定是 $T(\mathbf{v})=0$，我们可以将条件（a）和（b）合并成一个条件：

$$线性变换T(c\mathbf{v}+d\mathbf{w})=cT(\mathbf{v})+dT(\mathbf{w})$$

我们可以验证矩阵的乘法是线性的：$A(c\mathbf{v}+d\mathbf{w})=cA\mathbf{v}+dA\mathbf{w}$.
线性变换的限制很强。假设变换 $T$ 是对任意向量加上一个非零向量 ${\mathbf{u}}_0$，则 $T(\mathbf{v})=\mathbf{v}+{\mathbf{u}}_0,T(\mathbf{w})=\mathbf{w}+{\mathbf{u}}_0$，这个就不算线性的，我们对 $\mathbf{v}+\mathbf{w}$ 作变换 $T$ 会得到 $\mathbf{v}+\mathbf{w}+{\mathbf{u}}_0$，它并不等于 $T(\mathbf{v})+T(\mathbf{w})$：$$平移不是线性的\mathbf{v}+\mathbf{w}+{\mathbf{u}}_0不等于T(\mathbf{v})+T(\mathbf{w})=(\mathbf{v}+{\mathbf{u}}_0)+(\mathbf{w}+{\mathbf{u}}_0)$$只有当 ${\mathbf{u}}_0=0$ 时才是线性的，此时这个变换简化为 $T(\mathbf{v})=\mathbf{v}$，这个是恒等变换（identity transformation，没有任何变换，就如单位矩阵左乘向量一样）。这个当然是线性的，这种情况输入空间 $\text{V}$ 和输出空间 $\text{W}$ 是完全一样的。
“线性 + 平移（linear-plus-shift）” 变换 $T(\mathbf{v})=A\mathbf{v}+{\mathbf{u}}_0$ 称为 “仿射的（affine）”，尽管此时 $T$ 不是线性的，但是直线变换后仍为直线。移动计算机图形时，就可以使用仿射变换。

【例1】选择一个固定的向量 $\mathbf{a}=(1,3,4)$，令 $T(\mathbf{v})$ 是点积 $\mathbf{a}\cdot \mathbf{v}$：

$$\boxed{输入是\mathbf{v}=(v_1,v_2,v_3),输出是T(\mathbf{v})=\mathbf{a}\cdot \mathbf{v}=v_1+3v_2+4v_3}$$点积是线性的。输入 $\mathbf{v}$ 来自于三维空间，所以 $\text{V}={\text{R}}^3$. 输出只是数字，所以输出空间是 $\text{W}={\text{R}}^1$. 这个就相当于用行矩阵 $A=\left[\begin{array}{ccc}1& 3& 4\end{array}\right]$ 左乘 $\mathbf{v}$，即 $T(\mathbf{v})=A\mathbf{v}$.
现在我们能够很好的判断哪些变换是线性的了，如果输出包含平方、乘积或长度，$v_1^2,v_1{v}_2$ 或 $||\mathbf{v}||$，则 $T$ 就不是线性的。

【例2】长度 $T(\mathbf{v})=||\mathbf{v}||$ 不是线性的。线性条件（a）要求 $||\mathbf{v}+\mathbf{w}||=||\mathbf{v}||+||\mathbf{w}||$，条件（b）要求 $||c\mathbf{v}||=c||\mathbf{v}||$. 这两个条件均不满足！
条件（a）不成立：三角形的边满足三角不等式 $||\mathbf{v}+\mathbf{w}||\le ||\mathbf{v}||+||\mathbf{w}||$.
条件（b）不成立：长度 $||-\mathbf{v}||$ 是 $||\mathbf{v}||$ 而不是 $-||\mathbf{v}||$. 对于负数 $c$，线性不成立。

【例3】（旋转）$T$ 是将每个向量逆时针旋转 $30°$ 的变换，$T$ 的 “定义域（domain）” 是 $xy$ 平面（所有的输入向量 $\mathbf{v}$），$T$ 的 “值域（range）” 也是 $xy$ 平面（所有旋转了的向量 $T(\mathbf{v})$）。我们不适用矩阵来描述就是：平面逆时针旋转 $30°$.
旋转变换是线性的吗？答案是肯定的。我们可以将两个向量旋转后相加，旋转后的向量之和 $T(\mathbf{v})+T(\mathbf{w})$ 等于向量和的旋转 $T(\mathbf{v}+\mathbf{w})$. 在这个线性变换中，整个平面一起旋转。

二、线到线、三角形到三角形、基决定一切

Figure 8.1 展示了输入空间中从 $\mathbf{v}$ 到 $\mathbf{w}$ 的直线，也展示了输出空间中从 $T(\mathbf{v})$ 到 $T(\mathbf{w})$ 的直线。线性告诉我们：输入直线上的每一个点都映射到输出直线上；进一步地是：等间距的点映射为等间距的点。中点 $\mathbf{u}=\frac{1}{2}\mathbf{v}+\frac{1}{2}\mathbf{w}$ 映射为中点 $T(\mathbf{u})=\frac{1}{2}T(\mathbf{v})+\frac{1}{2}T(\mathbf{w})$.
另一个图上升一个维度，现在我们有三个顶点 ${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3$，这些输入有三个输出 $T({\mathbf{v}}_1),T({\mathbf{v}}_2),T({\mathbf{v}}_3)$，输入三角形映射为输出三角形，等间距的点仍然保持等间距（沿着边的和不在边上的都是如此），重心 $\mathbf{u}=\frac{1}{3}({\mathbf{v}}_1+{\mathbf{v}}_2+{\mathbf{v}}_3)$ 映射为重心 $T(\mathbf{u})=\frac{1}{3}(T({\mathbf{v}}_1)+T({\mathbf{v}}_2)+T({\mathbf{v}}_3))$.

$$线性性质可以扩展到三个向量或n个向量的组合：$$

$$\begin{array}{c}线性的\mathbf{u}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_n{\mathbf{v}}_n一定是变换为\\ \\ T(\mathbf{u})=c_{1}T({\mathbf{v}}_1)+c_{2}T({\mathbf{v}}_2)+\cdots +c_{n}T({\mathbf{v}}_n)\end{array}(\mathrm{8.1.1})$$

由 $2$ 个向量的性质得到推出 $3$ 个向量情形的证明：$T(c\mathbf{u}+d\mathbf{v}+e\mathbf{w})=T(c\mathbf{u})+dT(d\mathbf{v}+e\mathbf{w})$，然后对右边的这些项继续应用线性性质，可以得到 $cT(\mathbf{u})+dT(\mathbf{v})+eT(\mathbf{w})$.
$n$ 个向量的规则（8.1.1）给出线性变换最重要的性质：`

假设知道了一组基 ${\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_3$ 的全部变换 $T(\mathbf{v})$，那么就知道了这个空间中任意向量 $\mathbf{u}$ 的变换 $T(\mathbf{u})$.

理由是：空间中的任意向量 $\mathbf{u}$ 均是基向量 ${\mathbf{v}}_j$ 的线性组合，由线性性质可知，$T(\mathbf{u})$ 是输出 $T({\mathbf{v}}_j)$ 同样系数的线性组合。

【例4】变换 $T$ 是求输入的导数：$T(u)=\frac{\text{d}u}{\text{d}x}$. 如何求 $u=6-4x+3x^2$ 的导数？我们先从 $1,x$ 和 $x^2$ 的导数开始，这些就是基向量，它们的导数分别是 $0,1$ 和 $2x$，那么可以使用线性性质求基向量任意线性组合的导数：$$\frac{\text{d}u}{\text{d}x}=6(1的导数)-4(x的导数)+3(x^2的导数)=-4+6x$$微积分的内容都是基于线性性质的！微积分基础是先求出基本初等函数的导数，如 $x^n,\sin x,\cos x$ 和 $e^x$，然后再对它们所有的组合使用线性性质。
微积分中唯一特殊的法则是链式法则（chain rule），链式法则给出了复合函数 $f(g(x))$ 的导数。
$T(u)=\frac{\text{d}u}{\text{d}x}$ 的零空间：要得到零空间我们需要求解 $T(u)=0$. 当且仅当 $u$ 是一个常数函数时其导数为零。所以零空间是一维的，它是函数空间中的一条线 —— 包含特解 $u=1$ 所有的倍数。
$T(u)=\frac{\text{d}u}{\text{d}x}$ 的列空间：该例中输入空间包含所有的二次函数 $a+bx+c{x}^2$，输出空间（列空间）是所有的线性函数 $b+2cx$. 注意计数定理 $r+(n-r)=n$ 仍然成立。$$维数(列空间)+维数(零空间)=2+1=3=维数(输入空间)$$求导 $\frac{\text{d}}{\text{d}x}$ 对应的矩阵是什么？对于线性变换 $T=\frac{\text{d}}{\text{d}x}$，我们知道 $T$ 对基函数的作用：$${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3=1,x,x^2\frac{\text{d}{\mathbf{v}}_1}{\text{d}x}=0\frac{\text{d}{\mathbf{v}}_2}{\text{d}x}=1={\mathbf{v}}_1\frac{\text{d}{\mathbf{v}}_3}{\text{d}x}=2x=2v_2(\mathrm{8.1.2})$$三维的输入空间 $\text{V}$（二次函数）变换到二维的输出空间 $\text{W}$（线性函数）。如果将 ${\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3$ 当做向量，就可以得到变换矩阵$$\boxed{A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 2\end{array}\right]是求导变换T=\frac{\text{d}}{\text{d}x}的变换矩阵}(\mathrm{8.1.3})$$线性变换 $\frac{\text{d}u}{\text{d}x}$ 可以完美的由矩阵的乘法 $A\mathbf{u}$ 来解释。$$\begin{array}{l}输入\mathbf{u}\\ a+bx+c{x}^2\end{array}\begin{array}{cc}乘积A\mathbf{u}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 2\end{array}\right]\left[\begin{array}{c}a\\ b\\ c\end{array}\right]=\left[\begin{array}{c}b\\ 2c\end{array}\right]& 输出\frac{\text{d}u}{\text{d}x}=b+2cx\end{array}$$$T$ 和 $A$ 之间的联系（我们可以对每个线性变换都确定一个变换矩阵）依赖于输入基 $1,x,x^2$ 和输出基 $1,x$ 的选取。
下面看积分，它们给出导数的伪逆 $T^{+}$ ！ 这里不能写成 $T^{-1}$，那么也不能说 “ $T$ 的逆 ”，因为所有常数函数的导数都是 $0$，这是多对一的情况。

【例5】积分 $T^{+}$ 也是线性的：${\int }_0^x(D+Ex)\text{d}x=Dx+\frac{1}{2}E{x}^2$.
现在输入基是 $1,x$，输出基是 $1,x,x^2$，$T^{+}$ 对应的矩阵 $A^{+}$ 是 $3\times 2$ 的：$$\begin{array}{l}输入v\\ D+Ex\end{array}乘积A^{+}\mathbf{v}=\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1/2\end{array}\right]\left[\begin{array}{c}D\\ E\end{array}\right]=\left[\begin{array}{c}0\\ D\\ \frac{1}{2}E\end{array}\right]\begin{array}{l}输出v的积分\\ T^{+}(\mathbf{v})=Dx+\frac{1}{2}E{x}^2\end{array}$$微积分基本定理指出：积分是微分的（伪）逆。从线性代数来看，矩阵 $A^{+}$ 是矩阵 $A$ 的伪逆：$$A^{+}A=\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1/2\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 2\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]A{A}^{+}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right](\mathrm{8.1.4})$$常数函数的导数是零，零在 $A^{+}A$ 的对角线上。如果 $T=\frac{\text{d}}{\text{d}x}$ 没有一维的零空间，则微积分就不是微积分了（不再完整）。

三、变换的例子（大部分是线性的）

【例6】将任意三维向量投影到水平面 $z=1$ 上：向量 $\mathbf{v}=(x,y,z)$ 变换为 $T(\mathbf{v})=(x,y,1)$. 这个向量不是线性的。为什么呢？因为 $\mathbf{v}=0$ 甚至没有变换为 $T(\mathbf{v})=0$.

【例7】假设 $A$ 是一个可逆矩阵，则有 $T(\mathbf{v}+\mathbf{w})=A\mathbf{v}+A\mathbf{w}=T(\mathbf{v})+T(\mathbf{w})$. 另一个线性变换是用 $A^{-1}$ 左乘，这个给出了逆变换（inverse transformation）$T^{-1}$，它将每个向量 $T(\mathbf{v})$ 变换回 $\mathbf{v}$：$$T^{-1}(T(\mathbf{v}))=\mathbf{v}对应矩阵的乘积A^{-1}(A\mathbf{v})=\mathbf{v}$$如果 $T(\mathbf{v})=A\mathbf{v},S(\mathbf{u})=B\mathbf{u}$，则乘积 $T(S(\mathbf{u}))$ 对应乘积 $AB\mathbf{u}$.
下面讨论一个无可避免的问题：所有的从 $\text{V}={\text{R}}^n$ 到 $\text{W}={\text{R}}^m$ 的线性变换都可以由矩阵给出吗？ 当线性的 $T$ 是 “旋转” “投影” 或其它的变换，$T$ 总是有对应的矩阵 $A$ 吗？$T(\mathbf{v})$ 总是 $A\mathbf{v}$ 吗？
答案是肯定的！这是不从矩阵开始的线性代数的一种方法。在我们选择好一组输入基和输出基后，我们可以通过矩阵来描述线性变换。
注： 变换有自己的语言。从矩阵角度来看线性变换 $T(\mathbf{v})=A\mathbf{v}$，矩阵 $A$ 的列空间包含所有的输出 $A\mathbf{v}$，零空间包含所有的使 $A\mathbf{v}=0$ 时的输入；在变换语言中，这些对应的分别是 “值域（range）” 与 “核（kernel）”：
$T的值域：$ 所有的输出 $T(\mathbf{v})$. 值域对应列空间。
$T的核：$所有使得 $T(\mathbf{v})=0$ 的输入. 核对应零空间。
值域在输出空间 $\text{W}$ 中，核在输入空间 $\text{V}$ 中，当 $T$ 是用一个矩阵左乘，即 $T(\mathbf{v})=A\mathbf{v}$ 时，值域是列空间，核是零空间。

四、平面的线性变换

观察线性变换的作用比起定义它要更有趣。当一个 $2\times 2$ 的矩阵 $A$ 左乘 ${\text{R}}^2$ 中的所有向量时，我们可以观察它是如何作用的。我们下面以一个有 $11$ 个顶点的 “房子” 为例，这 $11$ 个向量 $\mathbf{v}$ 变换成 $11$ 个向量 $A\mathbf{v}$，连接 $\mathbf{v}$ 的直线变换成了连接 $A\mathbf{v}$ 的直线（从房子到房子的变换是线性的！）。对一个标准的房子应用 $A$ 会产生一个新房子 —— 可能伸缩或旋转或其它的不适合居住的房子。
这一部分是可视化的图像，不属于理论。下面展示了 $4$ 个房子和用于生成它们的矩阵。$H$ 的列是第一个房子的 $11$ 个顶点（$H$ 是 $2\times 12$ 的，以便于 plot2d 连接第 $11$ 个顶点和第 $1$ 个顶点），$A$ 左乘房子矩阵 $H$ 的 $11$ 个顶点将得到变换后房子 $AH$ 的顶点。
$$房子矩阵H=\left[\begin{array}{cccccccccccc}-6& -6& -7& 0& 7& 6& 6& -3& -3& 0& 0& -6\\ -7& 2& 1& 8& 1& 2& -7& -7& -2& -2& -7& -7\end{array}\right]$$
MATLAB 中画出标准房子的程序：

H = [-6 -6 -7 0  7 6 6 -3 -3 0 0 -6;-7 2 1 8 1 2 -7 -7 -2 -2 -7 -7];
x = H(1,:)'; y = H(2,:)';
axis([-10 10 -10 10]), axis('square')	% 坐标范围是x轴-10~10，y轴-10~10，坐标区域显示为正方形
plot(x, y,'o', x, y, '-');				% 连接线是实线，顶点是圆圈

五、主要内容总结

1. 变换 $T$ 将每个输入空间中的 $\mathbf{v}$ 映射为输出空间中的 $T(\mathbf{v})$.
2. 若 $T(\mathbf{v}+\mathbf{w})=T(\mathbf{v})+T(\mathbf{w})$ 且 $T(c\mathbf{v})=cT(\mathbf{v})$，则 $T$ 是线性的：直线映射为直线。
3. 线性变换将线性组合映射为线性组合：$T(c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\cdots +c_n{\mathbf{v}}_n)=c_{1}T({\mathbf{v}}_1)+c_{2}T({\mathbf{v}}_2)+\cdots +c_{n}T({\mathbf{v}}_n)$.
4. $T$ 为求导，$T^{+}$ 为积分都是线性的。$A$ 为 $m\times n$ 的矩阵，则 $T(\mathbf{v})=A\mathbf{v}$ 是将 ${\text{R}}^n$ 映射成 ${\text{R}}^m$.

六、例题

【例8】消元矩阵 $A=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$ 给出一个从 $(x,y)$ 到 $T(x,y)=(x,x+y)$ 的剪切变换（shearing transformation）. 如果输入向量填满一个正方形，画出变换后的正方形。
解： $x$ 轴上的点 $(1,0)$ 和 $(2,0)$ 进行 $T$ 变换后是与 $x$ 轴成 $45°$ 角直线上的点 $(1,1)$ 和 $(2,2)$. $y$ 轴上的点没有移动：$T(0,y)=(0,y)$，这个是 $\lambda =1$ 的特征向量。垂直的线向上滑动，这就是剪切，因此正方形变成了平行四边形。

【例9】若要非线性变换 $T$ 可逆，那么需要输出空间中的每个向量 $\mathbf{b}$ 都恰好对应输入空间的一个 $\mathbf{x}$：$T(\mathbf{x})=\mathbf{b}$ 总是恰好有一个解。下面这些变换（$x$ 为实数）哪些是可逆的？若可逆，则 $T^{-1}$ 是什么？它们不是线性的，甚至 $T_3$ 也不是。 当求解 $T(\mathbf{x})=\mathbf{b}$ 时，就是在求 $T$ 的逆：$$T_1(x)=x^2{T}_2(x)=x^3{T}_3(x)=x+9T_4(x)=e^x{T}_5(x)=\frac{1}{x}(x\ne 0)$$解： $T_1$ 不可逆：$x^2=1$ 有两个解并且 $x^2=-1$ 无解。
$T_4$ 不可逆因为 $e^x=-1$ 无解。（如果输出空间改为正数 $b$，则 $e^x=b$ 的逆就是 $x=\ln b$.）
注意 $T_5^2(x)=1$（取两次倒数）是恒等变换，但是 $T_3^2(x)=x+18$，$T_2^2(x)=x^9$，$T_4^2(x)=e^{e^x}$.
$T_2,T_3,T_5$ 可逆：$x^3=b,x+9=b$ 和 $\frac{1}{x}=b$ 都只有一个解：$$x=T_2^{-1}(b)=b^{1/3}x=T_3^{-1}(b)=b-9x=T_5^{-1}(b)=\frac{1}{b}$$
【例10】$H$ 是一个房子图形的矩阵，可以使用下面的函数 plot2d(H) 来绘制这个房子：$$房子矩阵H=\left[\begin{array}{cccccccccccc}-6& -6& -7& 0& 7& 6& 6& -3& -3& 0& 0& -6\\ -7& 2& 1& 8& 1& 2& -7& -7& -2& -2& -7& -7\end{array}\right]$$

function [] = plot2d(H)			% 定义函数 plot2d，输入参数是 H，无输出参数
    x = H(1,:)'; y = H(2,:)';	
    axis([-10 10 -10 10]), axis('square')
    plot(x, y, 'o', x, y, '-'); % 'o' 表示圆圈，'-' 表示实线段
end

（1）使用 plot2d(H) 画出这个房子矩阵的图，并画出以下矩阵作用后的图 plot2d(DH)，plot2d(BH)，plot2d(U*H)：$$D=\left[\begin{array}{cc}2& 0\\ 0& 1\end{array}\right]B=\left[\begin{array}{cc}0.7& 0.7\\ 0.3& 0.3\end{array}\right]U=\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$$（2）设变换 $T$ 满足 $T(\mathbf{v})=-\mathbf{v}+(1,0)$ 时，则经过此 “仿射变换” 后的图形如何？
（3）使用 Figure 8.2 中的矩阵来测试 plot2d(A’ * H) 和 plot2d(A’ * A * H).
解： 下面是 MATLAB画出这些图形的程序：

H = [-6 -6 -7 0 7 6  6 -3 -3  0  0 -6;
     -7  2  1 8 1 2 -7 -7 -2 -2 -7 -7];
figure('Name','原始房子H','NumberTitle','off');
plot2d(H);
D = [2 0; 0 1];
figure('Name','对角矩阵作用D*H','NumberTitle','off');
plot2d(D*H);
B = [0.7 0.7; 0.3 0.3];
figure('Name','秩一矩阵作用B*H','NumberTitle','off');
plot2d(B*H);
U = [1 1; 0 1];
figure('Name','上三角矩阵作用U*H','NumberTitle','off');
plot2d(U*H);
figure('Name','仿射变换T(v)=-v+(1,0)','NumberTitle','off');
plot2d(-H + [1;0]);
A = [cosd(35) -sind(35); sind(35) cosd(35)];        % cosd(),sind()为直接输入角度的函数
figure('Name','旋转矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','旋转矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);
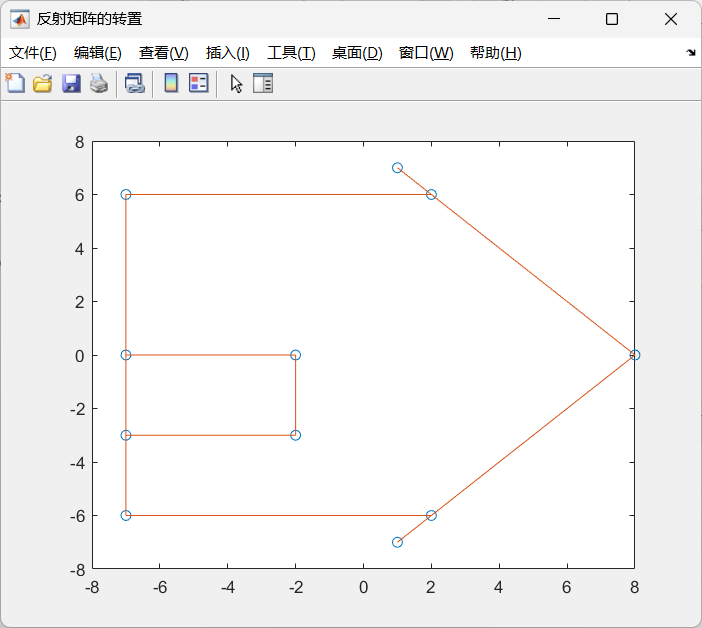
A = [0 1; 1 0];               % 反射矩阵
figure('Name','反射矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','反射矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);
A = [0.7 0.3; 0.3 0.7];        % 马尔可夫矩阵
figure('Name','马尔可夫矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','马尔可夫矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);

（1）MATLAB运行的图像如下：

（2）仿射变换：

（3）矩阵的转置：

【例11】下面代码是先创建一个包含 50 个角度的向量 theta, 然后生成一个单位圆，再使用变换 $T(\mathbf{v})=A\mathbf{v}$ 将这个单位圆变换成椭圆。最后绘制出这个单位圆和椭圆。

A = [2 1;1 2];                      % 变换矩阵A 
theta = 0:2*pi/50:2*pi;             % 0~2π共50个角度的theta向量
circle = [cos(theta); sin(theta)];  % 单位圆矩阵
ellipse = A * circle;               % 变换成椭圆
axis([-4 4 -4 4]); axis('square');
plot(circle(1, :), circle(2, :), ellipse(1, :), ellipse(2, :))  % 绘制单位圆和变换后的椭圆，其中circle(1, :)表示矩阵第一列的所有数据，此处是横坐标

解： 下面是 MATLAB运行后的图形