Codeforces Round 1024 (Div. 2) A ~ C 题解

A. Dinner Time

        一. 题意

        给定四个整数 n, m, p, q。判断是否存在一个长度为n的数组，符合两点条件。第一：数组之和为m。第二：每p个连续的元素和为q。

        二.算法

        构造

        三.思路

        我们可以观察到，题目想问我们（1.是否存在 2.满足条件），即问我们能否构造出这样的数组。因为p <= n，我们可以先试着分情况讨论，最简单的是 (p = n)。那么一定要满足 m = q。才能构造出。接着看(p < n)，会发现又有两种情况，第一种是比较简单，是(n % p == 0)，这种情况只有满足 (n / p) * q == m，才输出"YES"，第二种情况如下图：

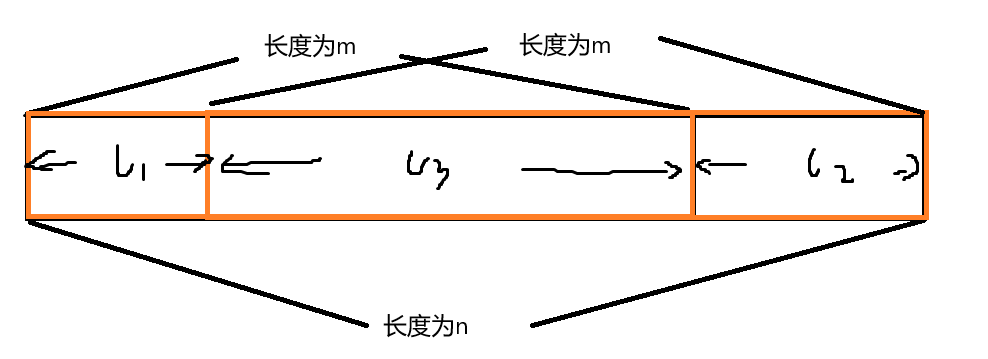
我们发现需要满足条件：1.  l1 段的元素与 l2 段的元素相同。2.  l3段的元素之和 + l1段的元素之和为q。3.  m * (n / m) + l2 == n。所以无论n和m的值，我们只需要调整l2的值即可使等式成立。

        四.代码

#include <iostream>
using namespace std;
 
void solve() {
	int n, m, p, q;
	cin >> n >> m >> p >> q;
	if (n == p) {
		if (m == q) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	else {
		if (n % p == 0) {
			if ((n / p) * q == m) cout << "YES" << endl;
			else cout << "NO" << endl;
		}
		else {
			cout << "YES" << endl;
		}
	}
}
 
int main() {
	int t;
	cin >> t;
	while (t--) {
		solve();
	}
}

---

B. The Picky Cat

        一.题意

        有一个长度为n的数组，可以进行一种操作任意次数，将数组中的一个元素乘负一。判断是否可以在任意操作次数后，让数组中的第一个元素成为中位数。

        二.算法

        基本的分类讨论 + 排序

        三.思路

        由于可以乘上负号，所以我们需要分别讨论 a1 和 -a1 是否可以成为中位数，两者有一者满足输出"YES"，都不满足输出 "NO"。回顾中位数的定义，我们需要将 a1 抽出，在剩余的元素中一半 小于 a1，一半大于 a1。所以我们统计在这里面所有可以大于 a1 的元素（注意每个元素都有正负需要判断）。

        四.代码

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) cin >> a[i];

    int a1 = a[0];
    int k = (n + 1) / 2;

    for (int j : {a1, -a1}) {
        int cnt1 = 0, cnt2 = 0;
        for (int i = 1; i < n; ++i) {
            int val = a[i];
            bool check1 = (val < j) || (-val < j);
            bool check2 = (val > j) || (-val > j);

            if (check1) cnt1++;
            if (check2) cnt2++;
        }
        if (cnt1 >= k - 1 && cnt2 >= (n - k)) {
            cout << "YES" << endl;
            return;
        }
    }
    cout << "NO" << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);

    int t;
    cin >> t;
    while (t--) solve();
}

---

C. Mex in the Grid

        一. 题意

        给定一个 n，需要排列 n * n 的一个网格，网格元素的范围从 0 到 n * n - 1。我们需要排列好这个网格，使所有子网格的 MEX 之和最大。

        二. 算法

        构造 + 贪心 + 预处理

        三.思路

        在处理有关 MEX 的问题时，我们需要注意 0 的特殊性，即所有的格子中只有含有0才可以以此为基础得到更大的数。所以为了得到更大的 MEX 之和，我们应该以0为中心展开方格的生成，那要如何生成呢？我们会发现只要按照 (右，下，左)、(左，上，右)的顺序交替生成，比如生成一个 2 * 2 的方格按照右，下，左的顺序，接着在2 * 2 的基础上再按照左，上，右的顺序生成。

        然后我们可以预处理好一个 500 * 500 的方格，根据 n 的值提取出其中的一部分就好。

        四.代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int ans[502][502];

void init() {
    memset(ans, -1, sizeof(ans));
    int x = 251, y = 251;
    ans[x][y] = 0;
    int num = 1;
    int dir = 0;
    int steps = 1;
    int dx[] = { 0, 1, 0, -1 };
    int dy[] = { 1, 0, -1, 0 };

    while (num < 250000) {
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < steps; j++) {
                x += dx[dir];
                y += dy[dir];
                ans[x][y] = num++;
            }
            dir = (dir + 1) % 4;
        }
        steps++;
    }
}

void solve() {
    int n;
    cin >> n;
    if (n == 1) {
        cout << "0" << endl;
        return;
    }
    int max_num = n * n - 1;
    int min_x = 502, max_x = -1, min_y = 502, max_y = -1;

    for (int x = 0; x < 502; x++) {
        for (int y = 0; y < 502; y++) {
            if (ans[x][y] != -1 && ans[x][y] <= max_num) {
                min_x = min(min_x, x);
                max_x = max(max_x, x);
                min_y = min(min_y, y);
                max_y = max(max_y, y);
            }
        }
    }

    for (int i = min_x; i <= max_x; i++) {
        for (int j = min_y; j <= max_y; j++) {
            if (j > min_y) cout << " ";
            cout << ans[i][j];
        }
        cout << endl;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    init();
    int t;
    cin >> t;
    while (t--) solve();
}