第八章 优先队列和堆
8-1 什么是优先队列
8-2 堆的基础表示
8-3 向堆中添加元素和Sift Up
8-4 从堆中取出元素和Sift Down
8-5 Heapify 和Replace
8-6 基于堆的优先队列
8-7 Leetcode上优先队列相关问题
8-8 Java中的PriorityQueue
8-9 和堆相关的更多话题和广义队列
8-1 什么是优先队列
我们在之前的两章向大家详细介绍了二分搜索树这种数据结构,同时我们使用二分搜索树实现了集合和映射这两个相对来讲更加高层的数据结构。树这种数据结构本身在计算机科学领域占有重要地位,因为树这种形状本身可以产生各种各样的拓展(绝不仅仅只有二分搜索树这一种),在面对不同的问题的时候,我们可以稍微改变或者限制树这种数据结构的性质,从而产生不同的数据结构,高效地解决不同的问题。接下来的四章内容,将要介绍四种不同的树的栗子,它们分别是:堆,线段树,字典树,并查集。
- 什么是优先队列?
普通队列:先进先出;后进后出
优先队列:与出队顺序和入队顺序无关;和优先级相关
举个栗子:1. 医院里病情严重的先治疗;2. 操作系统“动态”选择优先级最高的任务执行(动态:系统任务数量是变化的)3. 游戏中自动攻击敌人,比如周围敌人多的时候自动攻击哪个敌人
优先队列的接口:
- Interface Queue < E > <- - - - - - - - - - PriorityQueue < E >
- void enqueue (E)
- E dequeue ( )
- E getFront ( )
- int getSize ( )
- boolean isEmpty ( )
优先队列和普通队列接口功能的区别:
(1)出队元素优先级最高(而不是入队顺序最早的元素)
(2)队首元素优先级最高
优先队列的底层实现方式:

- 普通线性结构:选择优先级最高的元素时,复杂度为O(n) - - - - - - 动态数组,链表
- 顺序性结构:出队时选择最大元素,复杂度为O(1) - - - - - -对普通线性结构进行限制
- 堆结构:最差的复杂度为O(logn),优于二分搜索树。(完全二叉树的结构使其永远不会出现称为链表的情况,即复杂度为O(n))
8-2 堆的基础表示
堆也属于树结构,种类很多,此处主要介绍二叉堆(Binary Heap):

- 二叉堆是一个完全二叉树。
完全二叉树:把元素按顺序从左到右逐层排成树的结构。完全二叉树不一定是一个满二叉树。完全二叉树中,左节点必须是满的,右节点可以为空。 - 堆中某个节点的值总是不大于其父节点的值(最大堆)
最大堆中任意节点的值总是不大于其父节点的值(最小二叉堆同理)。
对于二叉堆来说,它只保证每一个节点的父亲节点比自己大,但是节点的大小和节点所处的层次之间是没有必然联系的(比如图中处于第二层的16,比处于第三层的19,17都小;第二层的13比第三层的所有元素都小)
用数组存储二叉堆:

我们可以用数组来存储二叉堆,每一个节点都标上号,标号的顺序是一个层次顺序。
对于数组中的每个节点,如何找到它的左右孩子节点?其实存在以下规律:
父节点的索引是子节点索引的1/2: parent(i) = i / 2
左子节点的索引是当前节点的2倍:left child (i) = 2 * i
右子节点的索引是当前节点的2倍+1:right child (i) = 2 * i + 1
最大堆的基础架构,代码实现如下:
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
// 返回堆中的元素个数
public int size(){
return data.getSize();
}
// 返回一个布尔值, 表示堆中是否为空
public boolean isEmpty(){
return data.isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index-0 doesn't have parent.");
return (index - 1) / 2;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index){
return index * 2 + 1;
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index){
return index * 2 + 2;
}
}
8-3 向堆中添加元素和Sift Up
- 向堆中添加元素涉及到堆的内部一个基础操作:Sift Up (堆中元素的上浮)
- 从树的角度看:添加元素相当于在层序遍历的最右端,也就是最下面一层的最后,再添加一个元素
从数组角度看:就是每次在数组索引为x的位置添加元素 - 然后,根据堆的性质(父节点大于子节点),与父节点比较,判断是否上浮。如果子节点大于其父节点,则交换两个元素。
// 向堆中添加元素
public void add(E e){
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k){
while(k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0 ){
data.swap(k, parent(k));
k = parent(k);
}
}
// 交换当前动态数组中,索引i, j两个元素的位置
public void swap(int i, int j){
if(i < 0 || i >= size || j < 0 || j >= size)
throw new IllegalArgumentException("Index is illegal.");
E t = data[i];
data[i] = data[j];
data[j] = t;
}
8-4 从堆中取出元素和Sift Down
在最大二叉堆中取出元素是一个下沉(Sift Down)的过程
- 提取出根节点位置的元素(index[0])
- 删除根节点后,将最后的叶节点移动到根节点位置,之后将其与两个子节点进行比较,与最大的子节点交换位置,持续迭代,直至满足完全二叉树的规则。
// 看堆中的最大元素
public E findMax(){
if(data.getSize() == 0)
throw new IllegalArgumentException("Can not findMax when heap is empty.");
return data.get(0);
}
// 取出堆中最大元素
public E extractMax(){
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
下沉的具体代码实现:
private void siftDown(int k){
while(leftChild(k) < data.getSize()){
int j = leftChild(k); // 在此轮循环中,data[k]和data[j]交换位置
if( j + 1 < data.getSize() &&
data.get(j + 1).compareTo(data.get(j)) > 0 )
j ++;
// data[j] 是 leftChild 和 rightChild 中的最大值
if(data.get(k).compareTo(data.get(j)) >= 0 )
break;
data.swap(k, j);
k = j;
}
}
在Main函数中测试上面两个操作:
import java.util.Random;
public class Main {
public static void main(String[] args) {
int n = 1000000;
MaxHeap<Integer> maxHeap = new MaxHeap<>();
Random random = new Random();
for(int i = 0 ; i < n ; i ++)
maxHeap.add(random.nextInt(Integer.MAX_VALUE));
int[] arr = new int[n];
for(int i = 0 ; i < n ; i ++)
arr[i] = maxHeap.extractMax();
for(int i = 1 ; i < n ; i ++)
if(arr[i-1] < arr[i])
throw new IllegalArgumentException("Error");
System.out.println("Test MaxHeap completed.");
}
}
- 这里堆的时间复杂度分析:
add 和 extractMax 的时间复杂度都是 O(logn)
8-5 Heapify 和Replace
- Relace:取出最大元素后,放入一个新元素
实现1:可以先extractMax,再add - - - - - -> 两次O(logn)的操作
实现2:可以直接将堆顶元素替换以后Sift Down - - - - - - > 一次O(logn)的操作
Replace 代码实现如下:
// 取出堆中的最大元素,并且替换成元素e
public E replace(E e){
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
- Heapify:将任意数组整理成堆的形状
Heapify从最后一个非叶子节点开始,对于完全二叉树而言近乎于一开始就抛弃了近一半的节点,对于剩下的近一半的节点进行sift Down操作。
将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn),而heapify的过程,算法复杂度为O(n)
所以,heapify的速度要更快。
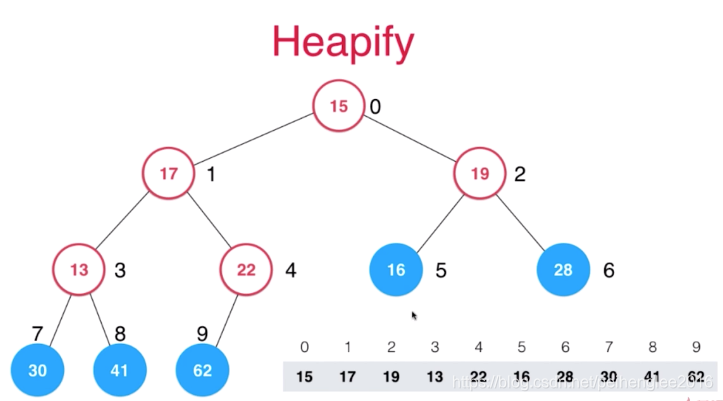
如图所示,对于当前数组来说,我们可以把它当成一个完全二叉树。图中所给的数组并不满足最大堆的性质,但是我们同样可以把它看作是一个完全二叉树,对于这个完全二叉树,我们从最后一个非叶子节点计算。在这个完全二叉树中,有五个叶子节点(30, 41, 62, 16, 28),相应的倒数第一个非叶子节点就是22这个元素所在节点,我们从这个节点开始,倒着从后向前不断进行Sift Down(下沉)这个操作。
这里会有一个经典面试问题:如何找出最后一个非叶子节点所对应的索引?方法非常简单:我们只需要找到最后一个节点它的索引,然后根据这个索引来找到它的父亲节点是谁就可以了。
具体流程如下:
接下来在索引为4的这个节点-22 进行下沉操作,这里62>22,交换位置,22所在节点已经是叶子节点,操作结束;之后看索引为3所在的节点-13进行下沉操作,这里41>30>13,交换位置,13所在节点成为叶子节点,操作结束;下面到了索引为2所在节点-19,这里28>19,交换位置,19所在节点成为叶子节点,操作结束;然后来看索引为1所在节点17,这里62>41>17,交换位置,位置交换后,17所在节点还有子节点,继续进行比较,发现22>17,继续交换位置,17这时候终于成为叶子节点,操作结束;接下来看索引为0的节点-15,它的左右孩子62>28>15,和62交换位置,依旧存在左右孩子节点,继续进行比较发现15<22<41,和41交换位置,交换位置后依旧有左右节点,继续进行比较,30>15>13,和30进行位置交换,至此15成为叶子节点,操作结束。
最终结果如下:

Heapify 代码实现如下:
public MaxHeap(E[] arr){
data = new Array<>(arr);
if(arr.length != 1){
for(int i = parent(arr.length - 1) ; i >= 0 ; i --)
siftDown(i);
}
}
测试函数:
import java.util.Arrays;
import java.util.Random;
public class Main {
private static double testHeap(Integer[] testData, boolean isHeapify){
long startTime = System.nanoTime();
MaxHeap<Integer> maxHeap;
if(isHeapify)
maxHeap = new MaxHeap<>(testData);
else{
maxHeap = new MaxHeap<>(testData.length);
for(int num: testData)
maxHeap.add(num);
}
int[] arr = new int[testData.length];
for(int i = 0 ; i < testData.length ; i ++)
arr[i] = maxHeap.extractMax();
for(int i = 1 ; i < testData.length ; i ++)
if(arr[i-1] < arr[i])
throw new IllegalArgumentException("Error");
System.out.println("Test MaxHeap completed.");
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int n = 1000000;
Random random = new Random();
Integer[] testData1 = new Integer[n];
for(int i = 0 ; i < n ; i ++)
testData1[i] = random.nextInt(Integer.MAX_VALUE);
Integer[] testData2 = Arrays.copyOf(testData1, n);
double time1 = testHeap(testData1, false);
System.out.println("Without heapify: " + time1 + " s");
double time2 = testHeap(testData2, true);
System.out.println("With heapify: " + time2 + " s");
}
8-6 基于堆的优先队列
需要将前面几章基础打好,这里理解起来其实没有啥问题的。
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
maxHeap = new MaxHeap<>();
}
@Override
public int getSize(){
return maxHeap.size();
}
@Override
public boolean isEmpty(){
return maxHeap.isEmpty();
}
@Override
public E getFront(){
return maxHeap.findMax();
}
@Override
public void enqueue(E e){
maxHeap.add(e);
}
@Override
public E dequeue(){
return maxHeap.extractMax();
}
}
8-7 Leetcode上优先队列相关问题
-
优先队列的经典问题:
在1,000,000个元素中选出前100名:n = 1,000,000, m = 100
使用排序算法,复杂度为O(nlogn);
使用优先队列,复杂度为O(nlogm); -
在n个元素中选出前m个元素:
使用优先队列,维护当前看到的前m个元素,需要使用最小堆
使用最小堆逻辑进行选择时,每次将最小的删除;如果使用最大堆,需要设定好优先级,如此最大最小就是相对的了。
Leetcode-347 前k个高频元素

Freq是priorityQueue中的对象,priorityQueue的底层是最大堆,取出优先级最高的元素。优先级最高的元素就是频次最低的那个元素。求出现的频率次数,需要用到映射Map,这里可以直接使用java提供的TreeMap来完成任务。
因为这里将compareTo重写了,shiftUp和shiftDown方法中都用到了compareTo方法(之前使用的是默认的)
private class Freq implements Comparable<Freq>{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
@Override
public int compareTo(Freq another){
if(this.freq < another.freq)
return 1;
else if(this.freq > another.freq)
return -1;
else
return 0;
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>();
for(int key: map.keySet()){
if(pq.getSize() < k)
pq.enqueue(new Freq(key, map.get(key)));
else if(map.get(key) > pq.getFront().freq){
pq.dequeue();
pq.enqueue(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.dequeue().e);
return res;
}
网站上提交的全部代码如下:
整体代码
8-8 Java中的PriorityQueue
Java中的PriorityQueue的内部默认是最小堆,此时它的优先级与最大堆相反:
- Java中的入队操作enqueue是add
- 获取数量操作getSize是size
- 拿到队首元素操作getFront是peek
- 出队操作dequeue是remove
自定义类中优先级的比较是比较容易的,但更多时候想改变的是Java标准库中的类的比较方式,此时我们自定义的priorityQueue是不胜任的,Java提供的priorityQueue类提供了一个解决方案;设置了一个实现compareTo比较器的私有类,覆盖compare(Freq a, Freq b)方法。
- 复习到本视频的时候,需要认认真真学习视频并且自己敲一遍。
Solution 1:
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.TreeMap;
public class Solution {
private class Freq implements Comparable<Freq>{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
public int compareTo(Freq another){
if(this.freq < another.freq)
return -1;
else if(this.freq > another.freq)
return 1;
else
return 0;
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>();
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(new Freq(key, map.get(key)));
else if(map.get(key) > pq.peek().freq){
pq.remove();
pq.add(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove().e);
return res;
}
private static void printList(List<Integer> nums){
for(Integer num: nums)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3};
int k = 2;
printList((new Solution()).topKFrequent(nums, k));
}
}
Solution 2:
import java.util.*;
public class Solution2 {
private class Freq{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
}
private class FreqComparator implements Comparator<Freq>{
@Override
public int compare(Freq a, Freq b){
return a.freq - b.freq;
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>(new FreqComparator());
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(new Freq(key, map.get(key)));
else if(map.get(key) > pq.peek().freq){
pq.remove();
pq.add(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove().e);
return res;
}
private static void printList(List<Integer> nums){
for(Integer num: nums)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3};
int k = 2;
printList((new Solution()).topKFrequent(nums, k));
}
}
Solution 3:
import java.util.*;
public class Solution3 {
private class Freq{
public int e, freq;
public Freq(int e, int freq){
this.e = e;
this.freq = freq;
}
}
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Freq> pq = new PriorityQueue<>(new Comparator<Freq>() {
@Override
public int compare(Freq a, Freq b) {
return a.freq - b.freq;
}
});
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(new Freq(key, map.get(key)));
else if(map.get(key) > pq.peek().freq){
pq.remove();
pq.add(new Freq(key, map.get(key)));
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove().e);
return res;
}
private static void printList(List<Integer> nums){
for(Integer num: nums)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3};
int k = 2;
printList((new Solution()).topKFrequent(nums, k));
}
}
Solution 4:
import java.util.*;
public class Solution4 {
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer a, Integer b) {
return map.get(a) - map.get(b);
}
});
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(key);
else if(map.get(key) > map.get(pq.peek())){
pq.remove();
pq.add(key);
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove());
return res;
}
private static void printList(List<Integer> nums){
for(Integer num: nums)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3};
int k = 2;
printList((new Solution()).topKFrequent(nums, k));
}
}
Solution 5:
import java.util.*;
public class Solution5 {
public List<Integer> topKFrequent(int[] nums, int k) {
TreeMap<Integer, Integer> map = new TreeMap<>();
for(int num: nums){
if(map.containsKey(num))
map.put(num, map.get(num) + 1);
else
map.put(num, 1);
}
PriorityQueue<Integer> pq = new PriorityQueue<>(
(a, b) -> map.get(a) - map.get(b)
);
for(int key: map.keySet()){
if(pq.size() < k)
pq.add(key);
else if(map.get(key) > map.get(pq.peek())){
pq.remove();
pq.add(key);
}
}
LinkedList<Integer> res = new LinkedList<>();
while(!pq.isEmpty())
res.add(pq.remove());
return res;
}
private static void printList(List<Integer> nums){
for(Integer num: nums)
System.out.print(num + " ");
System.out.println();
}
public static void main(String[] args) {
int[] nums = {1, 1, 1, 2, 2, 3};
int k = 2;
printList((new Solution()).topKFrequent(nums, k));
}
}
8-9 和堆相关的更多话题和广义队列
(1)二叉堆 - - - > d 叉堆(d-ary heap)
深度下降(层次变少),入队/出队的时间复杂度更低,但每次下沉Sift时考虑的子节点更多,复杂度会变高。

(2)索引堆
传统堆结构中只能看到堆首的元素,不能看到堆中的元素,索引堆可以解决这个问题;
最小生成树算法和最短路径算法都可以使用索引堆进行优化
(3)二项堆和斐波拉契堆(更高级的数据结构)
(4)广义队列:支持队列接口方法的(入队和出队操作)都可以理解为队列
出了普通队列,优先队列,栈,也可以理解成是一个队列:二分搜索树中前序遍历的递归算法和层序遍历算法的逻辑是一致的,区别只在于使用了不同的数据结构栈和队列。






















 263
263

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








