这是一款以 PEG (Progressive Edge Growth) 算法 为核心的 LDPC 校验矩阵生成器。PEG 通过“渐进式边增长”策略,在构造稀疏矩阵的同时有效抑制 4 环等短环的产生,提升码图性能,因而被广泛用于现代通信与机器学习译码研究。本工具将 PEG 算法封装为易用的交互界面,帮助你在几分钟内生成符合实验需求的 规则或非规则 LDPC 码,并自动导出用于神经网络 / GNN 训练的完整数据集。
除了矩阵生成,本项目还自带 矩阵特性分析、可视化、稀疏格式保存、Tanner 图导出 等一站式功能,开箱即用,适合科研、课程实验及工程验证场景。
PEG 算法(Progressive Edge Growth)是什么?
PEG 是 Hu-Eleftheriou-Arnold 在 2005 年提出的 逐边生长 构造法,用来生成 LDPC 校验矩阵对应的 Tanner 图。它一边添加边,一边最大化当前变量节点周围的最小环长(girth),因此能在 有限码长 下显著减少 4 环 / 6 环的数量,迭代译码时更稳定、更易收敛。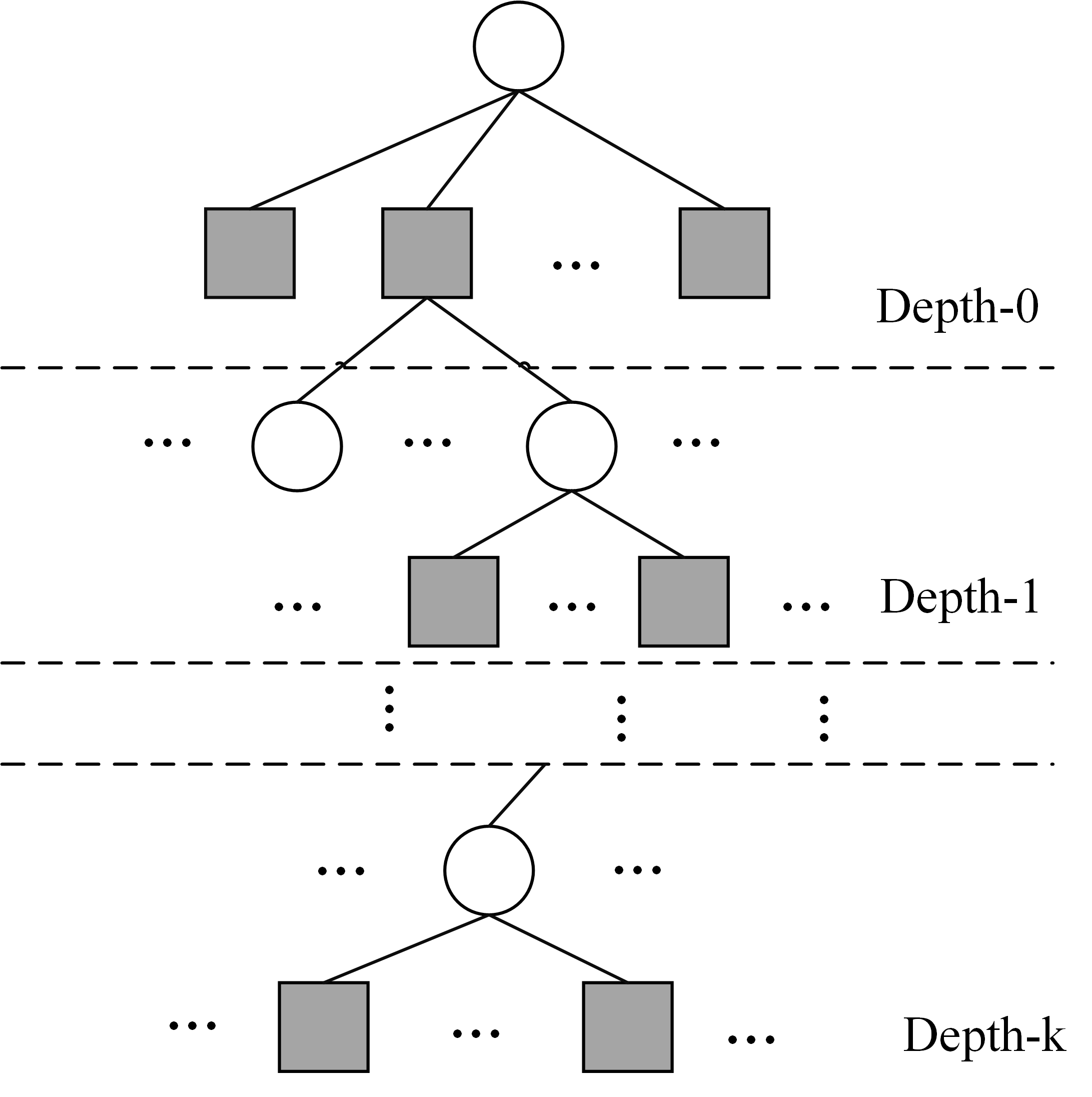
核心思路——“先均衡度数,再拉大环长”
-
输入:
-
变量节点数 n、校验节点数 m
-
变量节点度序列(规则码即常数 dᵥ;非规则码可自定义)
-
-
外层循环(按变量节点)
变量节点按度数升序遍历;低度节点先放边,可把宝贵的“长环位置”优先分给它们。 -
内层循环(按该节点第 k 条边)
-
第 1 条边:直接连到 当前校验度最小 的校验节点,保证整体行权重均衡。
-
后续边:
-
从该变量节点出发做一轮 BFS 扩展,逐层向外“长大”树;
-
找到 尚未出现在搜索树中的校验节点集合(即与此节点“最远”的校验节点);
-
在这个集合里再选 “度数最小” 的校验节点接边。
这样就把新边放在“离自己最远且行度最低”的位置,局部 girth ≥ 2·depth+2。
-
-
-
更新度数:edge 接完即刻更新行、列度,为下一条边提供最新信息。
为什么 PEG 效果好?
| 特性 | 原因 |
|---|---|
| 大 girth | “远节点”避免 4/6 环 |
| 均衡行权重 | 第 1 条边总连度最小校验节点 |
| 规则 / 非规则都支持 | 度序列可任意给定 |
| 可扩展到 QC、ACE、LPEG 等 | 只需在选边规则上加约束或打表 |
一句话总结
PEG 算法= “逐边生长 + BFS 选远邻 + 校验度最小”。它让你在纯软件脚本里就能快速得到大 girth、迭代译码友好的 LDPC 码图,是现代 LDPC 构造的黄金起点。
代码部分
运行示例:
python ldpc_generator.py
运行后选项:
================================================
LDPC码生成器 - 交互式版本
================================================
请选择要生成的LDPC码类型:
1. 小规模规则LDPC码 (64, 32, dv=3)
2. 中等规模规则LDPC码 (1000, 500, dv=3)
3. 5G-like LDPC码 (1944, 972, dv=3)
4. 非规则LDPC码 (1000, 500)
5. 自定义规则LDPC码
6. 自定义非规则LDPC码
7. 批量生成预设码
0. 退出
------------------------------------------------
请选择操作 (0-7):
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
LDPC码生成器 - 用于神经网络译码研究 (交互式版本, 修正版)
生成LDPC校验矩阵和相关数据集
"""
import numpy as np
import json
import os
from datetime import datetime
import matplotlib.pyplot as plt
import copy
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans'] # 使用黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 正常显示负号
def find_smallest(array):
"""返回 array 最小值的索引(稳定实现)"""
if len(array) == 0:
return 0
if len(array) == 1:
return 0
elif len(array) == 2:
return 0 if array[0] <= array[1] else 1
else:
mid = len(array) // 2
arrayA = array[:mid]
arrayB = array[mid:]
smallA = find_smallest(arrayA)
smallB = find_smallest(arrayB)
if arrayA[smallA] <= arrayB[smallB]:
return smallA
else:
return mid + smallB
class PEG:
"""Progressive Edge Growth算法的Python 3实现(左规则,右侧不强制)"""
def __init__(self, nvar, nchk, degree_sequence):
self.degree_sequence = degree_sequence
self.nvar = nvar
self.nchk = nchk
self.H = np.zeros((nchk, nvar), dtype=np.uint8)
self.sym_degrees = np.zeros(nvar, dtype=np.int32)
self.chk_degrees = np.zeros(nchk, dtype=np.int32)
def grow_edge(self, var, chk):
"""在 var 与 chk 之间加一条边"""
if self.H[chk, var] == 1:
return # 已有边则不重复
self.H[chk, var] = 1
self.sym_degrees[var] += 1
self.chk_degrees[chk] += 1
def bfs(self, var):
"""
以 var 为根进行层次遍历,返回一个"最小度且不在当前覆盖层"的校验节点。
退化时返回全局最小度校验节点(避免固定偏置到0)。
"""
var_list = np.zeros(self.nvar, dtype=np.uint8)
var_list[var] = 1
cur_chk_list = [0] * self.nchk
new_chk_list = [0] * self.nchk
chk_Q = []
var_Q = [var]
while True:
# 从已知变量节点扩展到校验节点
for _vars in var_Q:
# 遍历所有校验节点(可优化:用非零索引)
for i in range(self.nchk):
if self.H[i, _vars] == 1 and cur_chk_list[i] == 0:
new_chk_list[i] = 1
chk_Q.append(i)
var_Q = []
# 从新发现的校验节点扩展到变量节点
for _chks in chk_Q:
for j in range(self.nvar):
if self.H[_chks, j] == 1 and var_list[j] == 0:
var_list[j] = 1
var_Q.append(j)
chk_Q = []
# 若所有校验节点都已在覆盖层中,或层数不再扩展,则选择一个最小度的"未覆盖校验";
# 若不存在未覆盖校验,则退化为全局最小度校验节点。
if new_chk_list.count(1) == self.nchk or new_chk_list == cur_chk_list:
chosen = self.find_smallest_chk(cur_chk_list)
return chosen
else:
cur_chk_list = copy.copy(new_chk_list)
def find_smallest_chk(self, cur_chk_list):
"""
在"未覆盖校验节点"中选最小度的一个;若没有未覆盖者,则退化为全局最小度,避免系统性偏置到0号。
"""
candidates = [i for i, v in enumerate(cur_chk_list) if v == 0]
if candidates:
degs = self.chk_degrees[candidates]
return int(candidates[int(np.argmin(degs))])
# 退化选择:全局最小度校验节点
return int(np.argmin(self.chk_degrees))
def progressive_edge_growth(self, verbose=True):
for var in range(self.nvar):
if verbose and var % 50 == 0:
print(f"Edge growth at var {var}/{self.nvar}")
for k in range(self.degree_sequence[var]):
if k == 0:
# 第1条边连到"当前最小度的校验节点"
smallest_degree_chk = int(np.argmin(self.chk_degrees))
self.grow_edge(var, smallest_degree_chk)
else:
chk = self.bfs(var)
self.grow_edge(var, chk)
class LDPCMatrixGenerator:
"""LDPC校验矩阵生成器 - 生成LDPC校验矩阵、系统化与生成矩阵"""
def __init__(self):
self.H = None
self.G = None # 生成矩阵(k×n)
self.n = None # 码长
self.k = None # 信息位长度
self.m = None # 校验位行数(行数)
self.P = None # 系统形式 HΠ = [P | I_r] 中的 P(r×k),r为rank(H)
self.rank = None # rank(H)
def generate_regular_ldpc(self, n, m, dv, dc=None):
"""
生成左规则LDPC码(变量节点度为 dv)。不强制右规则。
n: 码长(变量节点数)
m: 校验节点数(H 的行数)
dv: 变量节点度数
dc: 目标校验节点平均度(仅显示),实际不强制
"""
if dc is None:
# 平均值(不强制)
dc = (n * dv) // m
if (n * dv) % m != 0:
print(f"提示:n*dv={n*dv} 不能被 m={m} 整除,右侧不会严格(平均度={dc})。")
print(f"生成规则({dv},{dc}) LDPC码: n={n}, m={m}")
degree_sequence = [dv] * n
peg = PEG(n, m, degree_sequence)
peg.progressive_edge_growth()
self.H = peg.H.astype(np.uint8)
self.n = n
self.m = m
# 验证度
actual_dv = float(np.mean(np.sum(self.H, axis=0)))
actual_dc = float(np.mean(np.sum(self.H, axis=1)))
print(f"实际平均度数: dv={actual_dv:.2f}, dc={actual_dc:.2f}")
# 计算生成矩阵
self._compute_generator_matrix()
return self.H
# ---------- GF(2) 工具函数 ----------
@staticmethod
def _gf2_rref(H):
"""
计算GF(2)行最简阶梯形(RREF),返回:
H_rref:行变换后的矩阵
pivots:主元列索引列表
"""
H = (H % 2).astype(np.uint8)
m, n = H.shape
row = 0
pivots = []
for col in range(n):
# 找主元行
pivot = None
for r in range(row, m):
if H[r, col]:
pivot = r
break
if pivot is None:
continue
# 交换到当前行
if pivot != row:
H[[row, pivot]] = H[[pivot, row]]
# 将该列除当前行外清零(GF(2))
for r in range(m):
if r != row and H[r, col]:
H[r, :] ^= H[row, :]
pivots.append(col)
row += 1
if row == m:
break
return H, pivots
def _convert_to_systematic_form(self, H):
"""
将H矩阵转换为系统形式(存在列置换 Π 使得 HΠ = [P | I_r],r=rank(H))
返回: (H_sys, P, perm, rank)
- H_sys: 行变换并按列重排后的矩阵(使主元列在最右边)
- P: 形状 (r, k) 的P子块
- perm: 长度为 n 的列置换(orig->sys 列顺序)
- rank: r = rank(H)
"""
H = (H % 2).astype(np.uint8)
m, n = H.shape
# 先做 RREF,得到主元列
H_rref, pivots = self._gf2_rref(H.copy())
r = len(pivots) # rank(H)
# 将主元列移到最右侧,非主元列在左侧
non_piv = [c for c in range(n) if c not in pivots]
new_order = non_piv + pivots # 前k列=非主元列,后r列=主元列
perm = np.array(new_order, dtype=int)
H_sys = H_rref[:, perm]
# 取出 P 块(r×k),注意:RREF 的后 r 列是单位阵(在前 r 行),其余行全0
k = n - r
if r == 0:
P = np.zeros((0, k), dtype=np.uint8)
else:
P = H_sys[:r, :k] # 只取前 r 行(有主元的行)
return H_sys, P, perm, r
def _compute_generator_matrix(self):
"""
计算系统形式的生成矩阵G。
通用做法:对任意满列秩/欠秩 H,求 rank r,令 k = n - r,
存在列置换 Π 使 HΠ = [P | I_r](r×r单位阵位于右侧),
则系统形式生成矩阵 G_sys = [I_k | P^T](k×n,处于"系统列顺序"),
最后将列顺序还原回原顺序:G[:, perm] = G_sys。
"""
try:
print("正在计算生成矩阵G...")
H_sys, P, perm, r = self._convert_to_systematic_form(self.H.copy())
self.rank = r
self.k = int(self.n - r)
self.P = P # (r, k)
if self.k < 0:
raise ValueError(f"计算到非法维度:k={self.k}")
# 处理极端情况:r=0 => H全零矩阵;此时任意G都满足 H G^T = 0
if r == 0:
self.G = np.eye(self.n, dtype=np.uint8)[:self.k, :] # 退化:取前k行为单位阵
ok = np.all(((self.H @ self.G.T) % 2) == 0)
print("✓ 生成矩阵验证通过: H * G^T = 0" if ok else "⚠ 警告: 生成矩阵验证失败")
return
# 在系统列顺序下构造 G_sys = [I_k | P^T]
I_k = np.eye(self.k, dtype=np.uint8)
G_sys = np.hstack([I_k, (P.T % 2)]).astype(np.uint8) # k × (k+r) = k × n
# 将列顺序还原到原始:perm 是 orig->sys 的新序,因此需要逆置换
G = np.zeros((self.k, self.n), dtype=np.uint8)
G[:, perm] = G_sys
self.G = G
# 验证 H * G^T = 0 (GF(2))
ok = np.all(((self.H @ self.G.T) % 2) == 0)
print("✓ 生成矩阵验证通过: H * G^T = 0" if ok else "⚠ 警告: 生成矩阵验证失败")
except Exception as e:
print(f"⚠ 生成矩阵计算失败: {e}")
print("将使用全零码字编码(仅用于占位,建议修复问题后再使用)")
self.G = None
self.P = None
def _verify_generator_matrix(self):
"""验证生成矩阵的正确性(保留接口)"""
if self.G is None or self.H is None:
return False
result = (self.H @ self.G.T) % 2
return np.all(result == 0)
def systematic_encode(self, messages):
"""
使用生成矩阵进行系统编码
messages: (batch_size, k) 信息位矩阵
返回: (batch_size, n) 码字矩阵
"""
if self.G is None:
print("警告: 生成矩阵不可用,返回全零码字(占位)。")
return np.zeros((messages.shape[0], self.n), dtype=np.uint8)
messages = (messages % 2).astype(np.uint8)
codewords = (messages @ self.G) % 2
return codewords.astype(np.uint8)
def generate_irregular_ldpc(self, n, m, dv_distribution):
"""
生成非规则LDPC码
dv_distribution: 变量节点度分布字典 {度数: 节点数}
"""
degree_sequence = []
for degree, count in dv_distribution.items():
if degree <= 0 or count < 0:
raise ValueError("度数必须>0且节点数>=0")
degree_sequence.extend([degree] * count)
if len(degree_sequence) != n:
raise ValueError(f"度分布总和({len(degree_sequence)})不等于n({n})")
print(f"生成非规则LDPC码: n={n}, m={m}")
print(f"度分布: {dv_distribution}")
peg = PEG(n, m, degree_sequence)
peg.progressive_edge_growth()
self.H = peg.H.astype(np.uint8)
self.n = n
self.m = m
# 计算生成矩阵
self._compute_generator_matrix()
return self.H
def analyze_matrix(self):
"""分析生成的LDPC矩阵特性"""
if self.H is None:
raise ValueError("请先生成LDPC矩阵")
var_degrees = np.sum(self.H, axis=0)
chk_degrees = np.sum(self.H, axis=1)
sH = int(np.sum(self.H))
m, n = self.H.shape
r = self.rank if self.rank is not None else int(min(m, n)) # 兜底
k = self.k if self.k is not None else int(n - r)
analysis = {
"dimensions": f"{m}x{n}",
"code_rate": float(k / n),
"density": float(sH / (m * n)),
"avg_variable_degree": float(np.mean(var_degrees)),
"avg_check_degree": float(np.mean(chk_degrees)),
"min_variable_degree": int(np.min(var_degrees)),
"max_variable_degree": int(np.max(var_degrees)),
"min_check_degree": int(np.min(chk_degrees)),
"max_check_degree": int(np.max(chk_degrees)),
"rank_H": int(r),
"k": int(k)
}
# 估计girth(最小环长)- 简化版本
analysis["estimated_girth"] = self._estimate_girth()
return analysis
def _estimate_girth(self, max_check=100):
"""估计矩阵的girth(最小环长,简化:仅检测4环)"""
m = self.m
upper = min(max_check, m)
for i in range(upper):
for j in range(i + 1, upper):
common = int(np.sum(self.H[i] & self.H[j]))
if common >= 2:
return 4
return ">4"
def visualize_matrix(self, save_path=None):
"""可视化LDPC矩阵"""
if self.H is None:
raise ValueError("请先生成LDPC矩阵")
plt.figure(figsize=(12, 8))
# 子图1:矩阵稀疏模式
plt.subplot(2, 2, 1)
plt.spy(self.H, markersize=1)
plt.title(f'LDPC矩阵稀疏模式 ({self.m}x{self.n})')
plt.xlabel('变量节点')
plt.ylabel('校验节点')
# 子图2:变量节点度分布
plt.subplot(2, 2, 2)
var_degrees = np.sum(self.H, axis=0)
plt.hist(var_degrees, bins=np.arange(var_degrees.min(), var_degrees.max() + 2) - 0.5)
plt.title('变量节点度分布')
plt.xlabel('度数')
plt.ylabel('节点数')
# 子图3:校验节点度分布
plt.subplot(2, 2, 3)
chk_degrees = np.sum(self.H, axis=1)
plt.hist(chk_degrees, bins=np.arange(chk_degrees.min(), chk_degrees.max() + 2) - 0.5)
plt.title('校验节点度分布')
plt.xlabel('度数')
plt.ylabel('节点数')
# 子图4:统计信息
plt.subplot(2, 2, 4)
r = self.rank if self.rank is not None else 0
k = self.k if self.k is not None else self.n - r
plt.text(0.1, 0.9, f'码率: {k / self.n:.3f}', transform=plt.gca().transAxes)
plt.text(0.1, 0.8, f'密度: {np.sum(self.H) / (self.m * self.n):.4f}', transform=plt.gca().transAxes)
plt.text(0.1, 0.7, f'平均变量度: {np.mean(var_degrees):.2f}', transform=plt.gca().transAxes)
plt.text(0.1, 0.6, f'平均校验度: {np.mean(chk_degrees):.2f}', transform=plt.gca().transAxes)
plt.axis('off')
plt.title('LDPC码统计信息')
plt.tight_layout()
if save_path:
plt.savefig(save_path, dpi=300, bbox_inches='tight')
print(f"图像已保存到: {save_path}")
else:
plt.show()
def save_for_nn_training(self, save_dir, dataset_name):
"""保存数据用于神经网络训练"""
if self.H is None:
raise ValueError("请先生成LDPC矩阵")
os.makedirs(save_dir, exist_ok=True)
# 保存校验矩阵
np.save(os.path.join(save_dir, f'{dataset_name}_H.npy'), self.H)
# 保存生成矩阵(如果可用)
if self.G is not None:
np.save(os.path.join(save_dir, f'{dataset_name}_G.npy'), self.G)
print(f"- {dataset_name}_G.npy: 生成矩阵")
# 保存为稀疏格式(节省空间)
saved_sparse = False
try:
from scipy.sparse import csr_matrix, save_npz
H_sparse = csr_matrix(self.H)
save_npz(os.path.join(save_dir, f'{dataset_name}_H_sparse.npz'), H_sparse)
saved_sparse = True
except ImportError:
print("警告:未安装scipy,跳过稀疏矩阵保存")
# 保存参数
params = {
'n': int(self.n),
'k': int(self.k) if self.k is not None else None,
'm': int(self.m),
'rank_H': int(self.rank) if self.rank is not None else None,
'code_rate': float((self.k / self.n) if self.k is not None else None),
'has_generator_matrix': self.G is not None,
'analysis': self.analyze_matrix(),
'timestamp': datetime.now().isoformat()
}
with open(os.path.join(save_dir, f'{dataset_name}_params.json'), 'w', encoding='utf-8') as f:
json.dump(params, f, indent=2, ensure_ascii=False)
# 生成Tanner图的邻接表示(用于GNN)
self._save_tanner_graph(save_dir, dataset_name)
print(f"数据已保存到: {save_dir}")
print(f"- {dataset_name}_H.npy: 校验矩阵")
if saved_sparse:
print(f"- {dataset_name}_H_sparse.npz: 稀疏格式校验矩阵")
print(f"- {dataset_name}_params.json: 参数文件")
print(f"- {dataset_name}_tanner_*.npy: Tanner图表示")
def _save_tanner_graph(self, save_dir, dataset_name):
"""保存Tanner图表示(用于图神经网络)"""
edges_v2c = []
edges_c2v = []
for i in range(self.m):
row = self.H[i]
nz = np.nonzero(row)[0]
for j in nz:
edges_v2c.append([j, i]) # 变量节点j到校验节点i
edges_c2v.append([i, j]) # 校验节点i到变量节点j
edges_v2c = np.array(edges_v2c, dtype=np.int32)
edges_c2v = np.array(edges_c2v, dtype=np.int32)
np.save(os.path.join(save_dir, f'{dataset_name}_tanner_v2c.npy'), edges_v2c)
np.save(os.path.join(save_dir, f'{dataset_name}_tanner_c2v.npy'), edges_c2v)
# ------------------ 菜单与交互 ------------------
def display_menu():
"""显示主菜单"""
print("\n" + "=" * 70)
print(" LDPC码生成器 - 交互式版本(修正版)")
print("=" * 70)
print("请选择要生成的LDPC码类型:")
print("1. 小规模规则LDPC码 (64, 32, dv=3) - 适合快速测试")
print("2. 中等规模规则LDPC码 (1000, 500, dv=3) - 标准测试")
print("3. 5G-like LDPC码 (1944, 972, dv=3) - 实际应用")
print("4. (3,6)规模规则LDPC码 (600, 300, dv=3, dc≈6) - 经典规模(右侧不强制)")
print("5. 码长128规则LDPC码 (128, 64, 码率≈0.5)")
print("6. 码长32规则LDPC码 (32, 16, 码率≈0.5)")
print("7. 码长8规则LDPC码 (8, 4, 码率≈0.5) - 微规模验证")
print("8. 码长648规则LDPC码 (648, 324, 码率≈0.5) - WiFi标准")
print("9. 非规则LDPC码 (1000, 500) - 高级研究")
print("10. 自定义规则LDPC码 - 自定义参数")
print("11. 自定义非规则LDPC码 - 自定义度分布")
print("12. 批量生成预设码 - 一次生成多种")
print("0. 退出")
print("-" * 70)
def generate_small_regular():
"""生成小规模规则LDPC码"""
print("\n生成小规模规则LDPC码...")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=64, m=32, dv=3)
# 分析并显示结果
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
# 询问是否保存
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'small_regular_64_32_3')
# 询问是否生成可视化
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_small_visualization.png')
return generator
def generate_medium_regular():
"""生成中等规模规则LDPC码"""
print("\n生成中等规模规则LDPC码...")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=1000, m=500, dv=3)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'medium_regular_1000_500_3')
return generator
def generate_5g_like():
"""生成5G-like LDPC码"""
print("\n生成5G-like LDPC码...")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=1944, m=972, dv=3)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', '5g_like_1944_972')
return generator
def generate_36_regular():
"""生成(3,6)规模规则LDPC码(右侧不强制,仅平均≈6)"""
print("\n生成(3,6)规模规则LDPC码...")
print("该码的特点:变量节点度数为3,校验节点平均度数≈6(未强制每个校验节点都等于6)")
n = 600 # 码长
m = 300 # 校验节点数:n*3/m=6,码率≈0.5
dv = 3
print(f"参数设置: n={n}, m={m}, dv={dv}, 期望dc≈{n*dv//m}, 码率≈{(n-m)/n:.1f}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'regular_600_300_3_6')
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_36_visualization.png')
return generator
def generate_128_regular():
"""生成码长128规则LDPC码(码率≈0.5)"""
print("\n生成码长128规则LDPC码...")
print("参数:码长n=128, 校验节点m=64, 码率≈0.5")
n = 128
m = 64
dv = 3
print(f"参数设置: n={n}, m={m}, dv={dv}, 期望dc≈{n*dv//m}, 码率≈{(n-m)/n:.1f}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'regular_128_64_3')
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_128_visualization.png')
return generator
def generate_32_regular():
"""生成码长32规则LDPC码(码率≈0.5)"""
print("\n生成码长32规则LDPC码...")
print("参数:码长n=32, 校验节点m=16, 码率≈0.5")
n = 32
m = 16
dv = 3
print(f"参数设置: n={n}, m={m}, dv={dv}, 期望dc≈{n*dv//m}, 码率≈{(n-m)/n:.1f}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'regular_32_16_3')
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_32_visualization.png')
return generator
def generate_8_regular():
"""生成码长8规则LDPC码(码率≈0.5)"""
print("\n生成码长8规则LDPC码...")
print("参数:码长n=8, 校验节点m=4, 码率≈0.5")
print("注意:这是一个极小规模的LDPC码,主要用于算法验证")
n = 8
m = 4
dv = 3
print(f"参数设置: n={n}, m={m}, dv={dv}, 期望dc≈{n*dv//m}, 码率≈{(n-m)/n:.1f}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'regular_8_4_3')
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_8_visualization.png')
return generator
def generate_648_regular():
"""生成码长648规则LDPC码(码率≈0.5)"""
print("\n生成码长648规则LDPC码...")
print("参数:码长n=648, 校验节点m=324, 码率≈0.5")
print("这是WiFi标准中常用的LDPC码长,适用于无线通信应用")
n = 648
m = 324
dv = 3
print(f"参数设置: n={n}, m={m}, dv={dv}, 期望dc≈{n*dv//m}, 码率≈{(n-m)/n:.1f}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'regular_648_324_3')
viz = input("是否生成可视化图像? (y/n): ").lower().strip()
if viz == 'y':
generator.visualize_matrix('ldpc_648_visualization.png')
return generator
def generate_irregular():
"""生成非规则LDPC码"""
print("\n生成非规则LDPC码...")
generator = LDPCMatrixGenerator()
# 度分布:大部分节点度为3,少数度为2和4(示例)
dv_dist = {2: 100, 3: 700, 4: 200}
generator.generate_irregular_ldpc(n=1000, m=500, dv_distribution=dv_dist)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', 'irregular_1000_500')
return generator
def generate_custom_regular():
"""生成自定义规则LDPC码"""
print("\n自定义规则LDPC码生成")
print("请输入参数(按Enter使用默认值):")
try:
n = input("码长 n (默认: 500): ").strip()
n = int(n) if n else 500
m = input(f"校验节点数 m (默认: {n // 2}): ").strip()
m = int(m) if m else n // 2
dv = input("变量节点度数 dv (默认: 3): ").strip()
dv = int(dv) if dv else 3
# 验证参数
if n <= 0 or m <= 0 or dv <= 0:
raise ValueError("参数必须为正数")
if m >= n:
raise ValueError("校验节点数必须小于码长")
print(f"\n生成参数: n={n}, m={m}, dv={dv}")
generator = LDPCMatrixGenerator()
generator.generate_regular_ldpc(n=n, m=m, dv=dv)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
name = input("输入数据集名称 (默认: custom_regular): ").strip()
name = name if name else "custom_regular"
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', name)
return generator
except ValueError as e:
print(f"参数错误: {e}")
return None
def generate_custom_irregular():
"""生成自定义非规则LDPC码"""
print("\n自定义非规则LDPC码生成")
try:
n = input("码长 n (默认: 500): ").strip()
n = int(n) if n else 500
m = input(f"校验节点数 m (默认: {n // 2}): ").strip()
m = int(m) if m else n // 2
print(f"\n需要定义{n}个变量节点的度分布")
print("格式:度数:节点数,用逗号分隔")
print("例如:2:100,3:300,4:100 表示100个度为2的节点,300个度为3的节点,100个度为4的节点")
dist_str = input("度分布: ").strip()
if not dist_str:
# 默认分布
dv_dist = {2: n // 5, 3: n * 3 // 5, 4: n // 5}
else:
dv_dist = {}
for pair in dist_str.split(','):
degree, count = pair.split(':')
dv_dist[int(degree)] = int(count)
# 验证度分布
total_nodes = sum(dv_dist.values())
if total_nodes != n:
print(f"警告:度分布总节点数({total_nodes})不等于n({n})")
if total_nodes < n:
# 自动补充度为3的节点
dv_dist[3] = dv_dist.get(3, 0) + (n - total_nodes)
print(f"自动调整后的度分布: {dv_dist}")
else:
raise ValueError("度分布总节点数超过n")
print(f"\n生成参数: n={n}, m={m}, 度分布={dv_dist}")
generator = LDPCMatrixGenerator()
generator.generate_irregular_ldpc(n=n, m=m, dv_distribution=dv_dist)
analysis = generator.analyze_matrix()
print(f"分析结果: {json.dumps(analysis, indent=2, ensure_ascii=False)}")
save = input("\n是否保存生成的LDPC码? (y/n): ").lower().strip()
if save == 'y':
name = input("输入数据集名称 (默认: custom_irregular): ").strip()
name = name if name else "custom_irregular"
os.makedirs('ldpc_data', exist_ok=True)
generator.save_for_nn_training('ldpc_data', name)
return generator
except ValueError as e:
print(f"参数错误: {e}")
return None
def batch_generate():
"""批量生成预设的LDPC码"""
print("\n批量生成模式")
print("将生成以下预设的LDPC码:")
print("1. 小规模规则LDPC码 (64, 32, dv=3)")
print("2. 中等规模规则LDPC码 (1000, 500, dv=3)")
print("3. 5G-like LDPC码 (1944, 972, dv=3)")
print("4. (3,6)规模规则LDPC码 (600, 300, dv=3, dc≈6)")
print("5. 码长128规则LDPC码 (128, 64, 码率≈0.5)")
print("6. 码长32规则LDPC码 (32, 16, 码率≈0.5)")
print("7. 码长8规则LDPC码 (8, 4, 码率≈0.5)")
print("8. 码长648规则LDPC码 (648, 324, 码率≈0.5)")
print("9. 非规则LDPC码 (1000, 500)")
confirm = input("\n确认批量生成? (y/n): ").lower().strip()
if confirm != 'y':
return
os.makedirs('ldpc_data', exist_ok=True)
generators = []
try:
print("\n[1/9] 生成小规模规则LDPC码...")
gen1 = LDPCMatrixGenerator()
gen1.generate_regular_ldpc(n=64, m=32, dv=3)
gen1.save_for_nn_training('ldpc_data', 'small_regular_64_32_3')
generators.append(("小规模规则", gen1))
print("\n[2/9] 生成中等规模规则LDPC码...")
gen2 = LDPCMatrixGenerator()
gen2.generate_regular_ldpc(n=1000, m=500, dv=3)
gen2.save_for_nn_training('ldpc_data', 'medium_regular_1000_500_3')
generators.append(("中等规模规则", gen2))
print("\n[3/9] 生成5G-like LDPC码...")
gen3 = LDPCMatrixGenerator()
gen3.generate_regular_ldpc(n=1944, m=972, dv=3)
gen3.save_for_nn_training('ldpc_data', '5g_like_1944_972')
generators.append(("5G-like", gen3))
print("\n[4/9] 生成(3,6)规模规则LDPC码...")
gen4 = LDPCMatrixGenerator()
gen4.generate_regular_ldpc(n=600, m=300, dv=3)
gen4.save_for_nn_training('ldpc_data', 'regular_600_300_3_6')
generators.append(("(3,6)规模规则", gen4))
print("\n[5/9] 生成码长128规则LDPC码...")
gen5 = LDPCMatrixGenerator()
gen5.generate_regular_ldpc(n=128, m=64, dv=3)
gen5.save_for_nn_training('ldpc_data', 'regular_128_64_3')
generators.append(("码长128规则", gen5))
print("\n[6/9] 生成码长32规则LDPC码...")
gen6 = LDPCMatrixGenerator()
gen6.generate_regular_ldpc(n=32, m=16, dv=3)
gen6.save_for_nn_training('ldpc_data', 'regular_32_16_3')
generators.append(("码长32规则", gen6))
print("\n[7/9] 生成码长8规则LDPC码...")
gen7 = LDPCMatrixGenerator()
gen7.generate_regular_ldpc(n=8, m=4, dv=3)
gen7.save_for_nn_training('ldpc_data', 'regular_8_4_3')
generators.append(("码长8规则", gen7))
print("\n[8/9] 生成码长648规则LDPC码...")
gen8 = LDPCMatrixGenerator()
gen8.generate_regular_ldpc(n=648, m=324, dv=3)
gen8.save_for_nn_training('ldpc_data', 'regular_648_324_3')
generators.append(("码长648规则", gen8))
print("\n[9/9] 生成非规则LDPC码...")
gen9 = LDPCMatrixGenerator()
dv_dist = {2: 100, 3: 700, 4: 200}
gen9.generate_irregular_ldpc(n=1000, m=500, dv_distribution=dv_dist)
gen9.save_for_nn_training('ldpc_data', 'irregular_1000_500')
generators.append(("非规则", gen9))
print("\n" + "=" * 60)
print("批量生成完成!生成的LDPC码统计:")
for name, gen in generators:
analysis = gen.analyze_matrix()
print(f"\n{name} LDPC码:")
print(f" - 维度: {analysis['dimensions']}")
print(f" - 码率: {analysis['code_rate']:.3f}")
print(f" - 密度: {analysis['density']:.4f}")
except Exception as e:
print(f"\n批量生成过程中出现错误: {e}")
import traceback
traceback.print_exc()
def main():
"""主函数 - 交互式LDPC码生成"""
print("LDPC码生成器启动...")
while True:
display_menu()
try:
choice = input("请选择操作 (0-12): ").strip()
if choice == '0':
print("感谢使用LDPC码生成器!")
break
elif choice == '1':
generate_small_regular()
elif choice == '2':
generate_medium_regular()
elif choice == '3':
generate_5g_like()
elif choice == '4':
generate_36_regular()
elif choice == '5':
generate_128_regular()
elif choice == '6':
generate_32_regular()
elif choice == '7':
generate_8_regular()
elif choice == '8':
generate_648_regular()
elif choice == '9':
generate_irregular()
elif choice == '10':
generate_custom_regular()
elif choice == '11':
generate_custom_irregular()
elif choice == '12':
batch_generate()
else:
print("无效选择,请重新输入!")
except KeyboardInterrupt:
print("\n\n用户中断操作")
break
except Exception as e:
print(f"\n操作过程中出现错误: {e}")
import traceback
traceback.print_exc()
# 询问是否继续
if choice != '0':
continue_choice = input("\n是否继续使用生成器? (y/n): ").lower().strip()
if continue_choice != 'y':
print("感谢使用LDPC码生成器!")
break
if __name__ == "__main__":
main()
代码里的 PEG 实现细节
-
PEG.progressive_edge_growth():外层遍历变量节点,内层按度数degree_sequence[var]调用-
k==0→find_smallest()找行度最小的校验节点 -
k>0→bfs(var)搜索可选校验集合,再选行度最小者
-
-
grow_edge()同时更新H、度计数和辅助索引表; -
_estimate_girth()用“是否存在双共边的行对”粗判 4 环,用作快速提示





















 723
723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








