8.2 向量数量积与向量积（点乘与叉乘）

本篇内容依然是向量的运算，只不过不属于线性运算，内容包括向量的数量积与向量积。

一、向量的数量积（内积、点乘，参与运算的是向量，结果是数）

（一）问题产生的背景与表达

（二）向量数量积定义（几何）
向量数量积表示的运算就是两个向量的模乘以两个向量夹角的余弦

（三）数量积的性质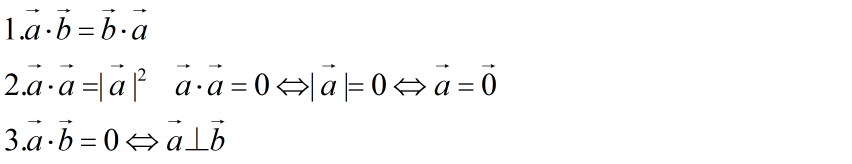
（四）向量的数量积的代数描述

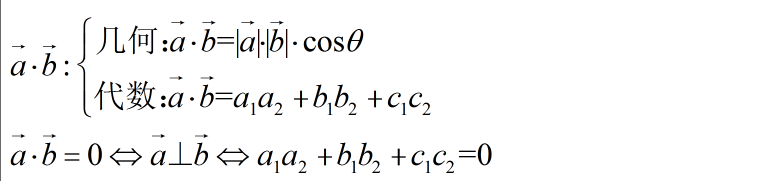
例题

例1

二、向量积（叉积、叉乘，参与运算的是向量，结果是向量）

（一）产生的背景：法向量
空间中向量a、b构成一个平面，找到一个向量，既垂直于a向量，又垂直于b向量，这个向量就是法向量
向量向量积的定义

• 几何定义

  • 方向：右手准则

  • 大小：

注解
①两个向量叉乘为0向量则两个向量平行，充要条件

---

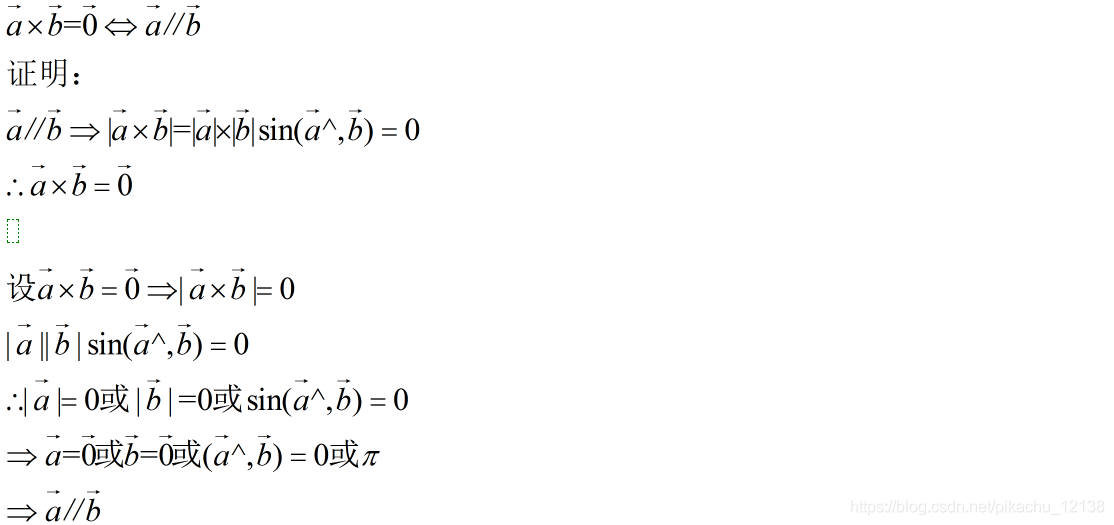
②a、b两个向量叉乘的结果既垂直于a向量又垂直于b向量

---

③叉乘运算不满足交换律，满足负交换律

右手准则验证
④

• 代数描述
  
  上面计算的这个代数描述是要记住的 [手动滑稽]
  记不住哈，给个方法
  

例题

例1

---

*重要定理

例题

例2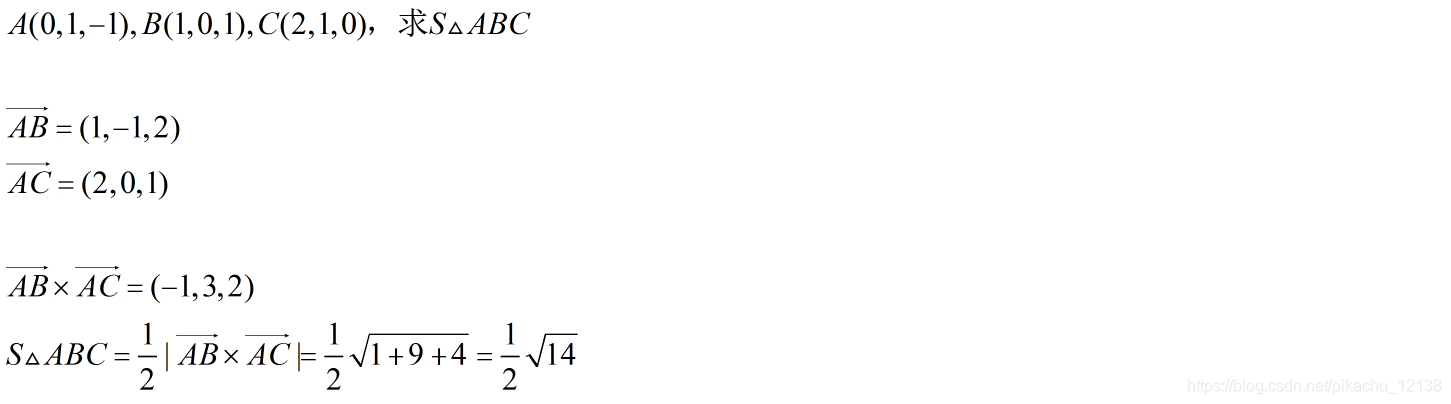

总结

因为作者总是分不清点乘和叉乘，所以这边写点区分它俩的总结。

点乘是数量积又叫内积，向量的计算结果是一个数
叉乘是向量积又叫叉积，向量的计算结果还是向量

点乘和叉乘都要用到的向量的模和夹角
点乘对应cos，数量积为零，两向量垂直
叉乘对应sin，向量积为零，两向量平行

本篇完。