9.1 多元微分学及应用——多元函数的基本概念

一、平面点集

• 去心邻域：比对数轴的去心邻域概念，平面上一个点的去心邻域就是以该点为中心取一个大于0的值为半径的圆标识的范围（不包括圆心点和邻域边界）

• 邻域：去心邻域+圆心点

• 开集：所谓开集，即点集无孤立点，同时点集无边界点，比对开区间，即开集取不到边界，对于点集内任意点M，存在δ>0,使M的邻域包含于该点集内。

• 连通：点集没有被完全分隔开
  

• 开区域：连通的开集

• 闭区域：开区域+区域边界

多元函数的概念

• 多元函数：还是比对一元函数理解，一元函数是有一个自变量x和一个因变量y，伴随x的变化，总存在唯一的y与之对应（x与y之间带关系可以是一对一、多对一但不能一对多）；多元函数就是自变量不止一个，仅此而已
• 定义域：自变量的取值范围
• 值域：定义域中所有自变量的值对应的所有的函数值组成的集合

多元函数的极限

emmm，我们还是比对一元函数带极限来理解吧，我这边做个简单回顾，如果忘记了，请翻阅本系列博客第一章

• 一元函数的极限
• 二元函数的极限

是不是差不多？是差不多，唯一不同的地方，一元函数取去心邻域时可以看作实在数轴上取，二元函数取去心邻域就变成了我们本篇中介绍的去心邻域的状态了，是这样的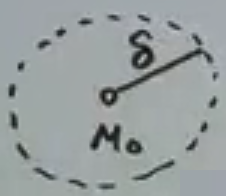

注解

二元函数和一元函数的去心邻域取法的不同决定了二元函数（或者说多元函数）极限的复杂性，我们看上面这个图，研究一元函数带极限时，只要讨论函数在某一点的左右极限就可以了，但是对于多元函数，我们根据上面带图可以看出，极限的方向有无数个。

例题

例1
例2
例3

四、多元函数的连续性与性质

• 连续性：极限值=函数值，由于上述带一元函数与多元函数的差异，所以多元函数不用考虑左右极限

多元函数在有界闭区域上的性质
比对一元函数在闭区间上的性质

• 最值定理
• 有界定理
• 介值定理
• 零点定理

本篇完。