矩阵相乘的两种方法

///
/*
名称：矩阵相乘的两种方法
说明：最近，在复习线性代数的时候，老师说到矩阵A*B，可以把B转化为一个个列向量b1，b2，b3分别与A矩阵相乘。这和我以前的想法不同，以前的想法都是按照标准公式A的第一行*B的第一列，然后相加。今天所认识的，虽然在计算机上计算过程并没有太大的区别，但在线性代数上可以更好的理解什么是线性变换（虽然我现在理解的还不是很深刻）。于是，用一个普通的C++程序实现，算是加强印象吧。
这两种方法我分别把他们叫做行相乘，列相乘算法。
如下图所示：

![列相乘](https://img-blog.csdn.net/20170626204749777?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvcGxtMTk5NTEzMTAw/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)

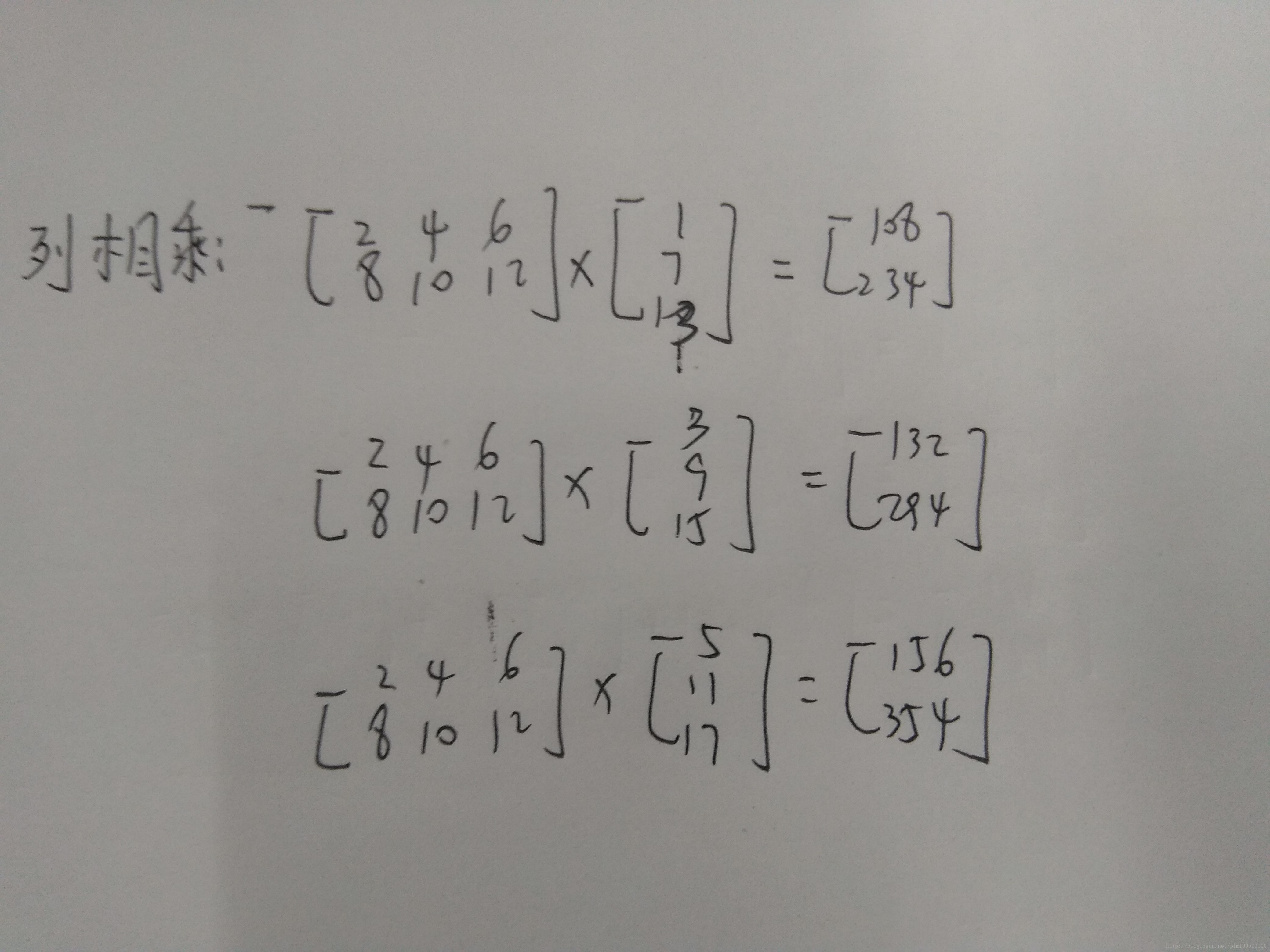
此种两种算法还可以应用于并行算法中，有时间可以实现以下。

*/
//

#include<iostream>
using namespace std;

class MultiMatrix
{
public:


    /*m代表A矩阵的行数，n代表A矩阵的列数（也代表B矩阵的行数）,p代表（B矩阵的列数）
        i控制A矩阵的行数变化，j控制B矩阵的列数变化，k控制A矩阵的列数变化（同时控制B矩阵的行数变化）
    */
    void RowMulMatrix(int A[][3],int B[][3],int m,int n,int p)
    {
        int res[m][n];      //保存最终结果
        int sum;

        //矩阵相乘计算
        for(int i = 0;i<m;++i)      //后计算A的行
        {
            for(int j = 0;j<n;++j)     //先计算B的列
            {
                sum = 0;
                for(int k = 0;k<p;++k)
                {
                    sum = sum + A[i][k]*B[k][j];
                }
                res[i][j] = sum;
            }
        }

        //输出结果
        for(int i = 0;i<m;++i)
        {
            for(int j = 0;j<n;++j)
            {
                if(j == 0)
                    cout<<res[i][j];
                else
                    cout<<" "<<res[i][j];
            }
            cout<<endl;
        }
    }


    void ColMulMatrix(int A[][3],int B[][3],int m,int n,int p)
    {

        int res[m][n];      //保存最终结果
        int sum;


        for(int j = 0;j<p;++j)      //后计算B的列
        {
            for(int i = 0;i<m;++i)      //先计算A的行
            {
                sum = 0;
                for(int k = 0;k<n;++k)
                {
                    sum = sum+A[i][k]*B[k][j];
                }

                res[i][j] = sum;
            }

        }

         //输出结果
        for(int i = 0;i<m;++i)
        {
            for(int j = 0;j<n;++j)
            {
                if(j == 0)
                    cout<<res[i][j];
                else
                    cout<<" "<<res[i][j];
            }
            cout<<endl;
        }
    }

};

int main()
{
    int A[2][3] = {2,4,6,
                   8,10,12};

    int B[3][3] = {1,3,5,
                   7,9,11,
                   13,15,17};

    //测试
    MultiMatrix ex;
    //
    ex.RowMulMatrix(A,B,2,3,3);
    cout<<endl;
    ex.ColMulMatrix(A,B,2,3,3);

  return 0;

}