拉普拉斯方程和泊松方程的MATLAB可视化

• 泊松方程类比二维热传导方程

制作的原理是泊松方程类比二维热传导方程，首先列出方程：

∂u/∂t=a^2（∂^2 u/∂x^2+∂^2 u/∂y^2）+f（x,y,t）

在这个方程中f（x，y，t）是热源，参数a^2是一个常数。已知热传导方程随时间演变，会演变成一个温度与时间无关，趋于稳定的状态。自然条件下，热源也会演变成一个与时间无关的函数。

在matlab上程序如下:

clear,clc,close all

dx=0.05;

Lx=1;

x=0:dx:Lx;

dy=0.05;

Ly=2;

y=0:dy:Ly;

A1=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);

A2=-2*eye(length(y))+diag(ones(1,length(y)-1),1)+diag(ones(1,length(y)-1),-1);

dt=0.0001;

t=0:dt:1;

[Y,X]=meshgrid(y,x);%十分重要不同y构成行向量，不同x构成列向量

U0=exp(-10*((X-1/2).^2+(Y-1/2).^2));

U=U0;

a=1;

for n=1:length(t)-1

    U=U+a^2*(1/dx^2*A1*U+1/dy^2*U*A2)*dt;

    if mod(n,100)==1

    surf(X,Y,U)

    axis([x(1) x(end) y(1) y(end) 0 1])

    getframe;

    end

End

在上述程序中设置边界为零，运行后得到图像：

根据上面的方法，同理求静电场的拉普拉斯方程。

与时间无关时，方程为：

∂^2 u/∂x^2+∂^2 u/∂y^2）=−1/a^2f（x，y）

此时将 将a^2类比ε,f(x,y)类比ρ(x,y)

得到泊松方程(∂^2u/∂x^2+∂^2u/∂y^2)=−ρ(x,y)/ε

• 拉普拉斯方程

上文中我们得到了泊松方程，由泊松方程推导出 拉普拉斯方程表达式。即：

当ρ(x,y)=0时

(∂^2u/∂x^2+∂^2u/∂y^2)=0,为拉普拉斯方程

当ρ(x,y)≠0时

(∂^2u/∂x^2+∂^2u/∂y^2)=−ρ(x,y)/ε,为泊松方程

在matlab上运行程序如下：

clear,clc,close all

dx=0.02;

Lx=1;

x=0:dx:Lx;

dy=0.02;

Ly=1;

y=0:dy:Ly;

m1=sin(pi*x/Lx);m2=sin(pi*x/Lx);m3=0*y';m4=0*y';

A1=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);

A2=-2*eye(length(y))+diag(ones(1,length(y)-1),1)+diag(ones(1,length(y)-1),-1);

dt=0.0001;

t=0:dt:1;

[Y,X]=meshgrid(y,x);%十分重要不同y构成行向量，不同x构成列向量

U0=exp(-10*((X-1/2).^2+(Y-1/2).^2));

U=U0;

e0=1;

rou=0;

for n=1:length(t)-1

    U=U+e0^2*(1/dx^2*A1*U+1/dy^2*U*A2+rou)*dt;

    U(:,1)=m1;

    U(:,end)=m2;

    U(1,:)=m3;

    U(end,:)=m4;

    if mod(n,100)==1

    surf(X,Y,U)

    axis([x(1) x(end) y(1) y(end) -1 3])

    getframe;

    end

end

figure

[Ex,Ey]=gradient(-U,dx,dy);%求电场强度

contour(X,Y,U);%画等势线

hold on

quiver(X,Y,Ex,Ey);%画矢量

图像会由静电场边界演变成与时间无关的静电场的结果。

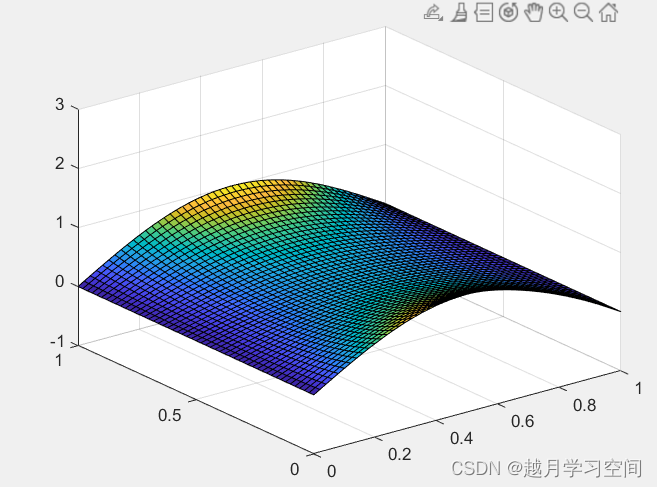
在程序中，电场强度的计算采用的是梯度的计算方法。

以上是拉普拉斯方程。

在计算泊松方程时我们加入了两个点电荷，一个正电荷和一个负电荷。

在matlab中运行程序如下：

clear,clc,close all

dx=0.02;

Lx=1;

x=0:dx:Lx;

dy=0.02;

Ly=1;

y=0:dy:Ly;

m1=sin(pi*x/Lx);m2=sin(pi*x/Lx);m3=0*y';m4=0*y';

A1=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);

A2=-2*eye(length(y))+diag(ones(1,length(y)-1),1)+diag(ones(1,length(y)-1),-1);

dt=0.0001;

t=0:dt:1;

[Y,X]=meshgrid(y,x);%十分重要不同y构成行向量，不同x构成列向量

U0=exp(-10*((X-1/2).^2+(Y-1/2).^2));

U=U0;

e0=1;

D=0.1;

rou=exp(-((X-1/2).^2+(Y-1/2).^2)/D^2);

for n=1:length(t)-1

    U=U+(e0^2*(1/dx^2*A1*U+1/dy^2*U*A2)+rou)*dt;

    U(:,1)=m1;

    U(:,end)=m2;

    U(1,:)=m3;

    U(end,:)=m4;

    if mod(n,100)==1

    surf(X,Y,U)

    axis([x(1) x(end) y(1) y(end) -1 3])

    getframe;

    end

end

figure

[Ex,Ey]=gradient(-U,dx,dx);%求电场强度

contour(X,Y,U);%画等势线

hold on

quiver(X,Y,Ex,Ey);%画矢量

axis equal

得到图像：

• 第一类边界条件

1. 矩形边界

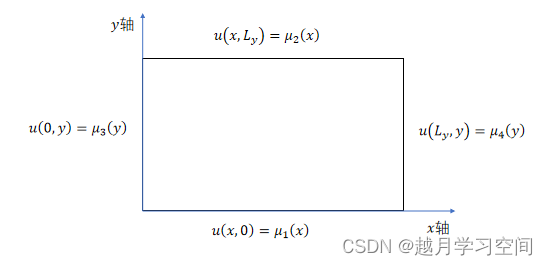1. 圆形边界

圆形边界一般可得到圆面上的电势分布情况：u(x^2+y^2=R^2)=μ(θ)

但在matlab中运用的是离散化的处理方法，无法直接赋值到圆形边界上。因此，我们引入一个矩形边界，框住圆形边界，将圆形与框架中的四个空白部分赋值为：u(x^2+y^2≥R^2)=μ(θ)

clear,clc,close all

dx=0.02;

R=1;

x=-R:dx:R;

y=-R:dx:R;

A1=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);

A2=-2*eye(length(y))+diag(ones(1,length(y)-1),1)+diag(ones(1,length(y)-1),-1);

dt=0.0001;

t=0:dt:1;

[X,Y]=meshgrid(x,y);

U0=exp(-10*((X-1/2).^2+(Y-1/2).^2));

U=U0;

e0=1;

D=1;

% rou=10*exp(-((X-1/2).^2+(Y).^2)/D^2)-10*exp(-((X+1/2).^2+(Y).^2)/D^2);

rou=0;

theta=angle(X+1i*Y);

G=X.^2+Y.^2>=R.^2;

for n=1:length(t)-1

    U=U+(e0^2*(1/dx^2*A1*U+1/dx^2*U*A2)+rou)*dt;

    U(G)=sin(theta(G));

    if mod(n,100)==1

    surf(X,Y,U)

    axis([x(1) x(end) y(1) y(end) -1 3])

    axis equal

    getframe;

    end

end

%G1=X.^2+Y.^2>R^2;

U(G1)=NaN;

[Ex,Ey]=gradient(-U,dx,dx);

contour(X,Y,U)

hold on

quiver(X,Y,Ex,Ey)

plot(cos(0:pi/50:2*pi),sin(0:pi/50:2*pi))

hold off

运行前部分后得到图像：

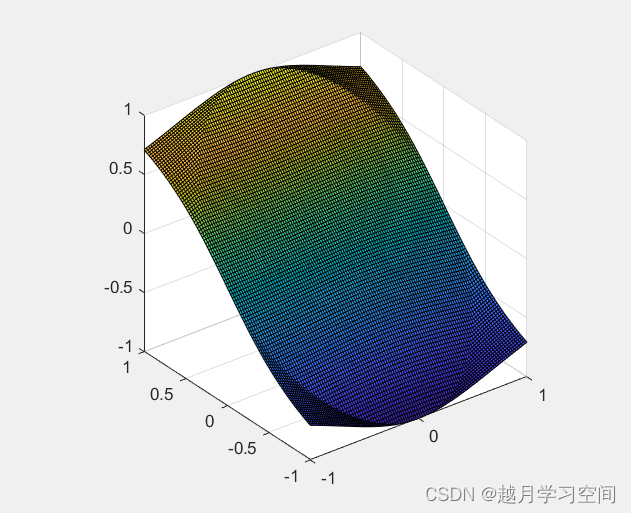
（在图像中我们对四个空白区域赋值为同一个结果，因此有等势线。）

但我们的最终目的是去除圆外的四个空白区域，也就是程序中注释的部分：

G1=X.^2+Y.^2>R^2;

U(G1)=NaN;

（也就是在矩阵中不作为一个数，因此不会出现在图像中。）

程序中我们设置了10倍的正电荷和10倍的负电荷

rou=10*exp(-((X-1/2).^2+(Y).^2)/D^2)-10*exp(-((X+1/2).^2+(Y).^2)/D^2);

删去电荷后便得到了拉普拉斯方程。。

• 第二类边界条件

1. 拉普拉斯方程

第二类边界条件需界定有解条件，即对原定封闭体积做积分，由于计算的是二维空间图像，因此积分为面积分

由高斯公式，将体积分变为面积分

梯度*向量为方向导数

整个面积分为0

以上便是它的有解条件

clear,clc,close all

dx=0.02;

Lx=1;

x=0:dx:Lx;

dy=0.02;

Ly=1;

y=0:dy:Ly;

m1=sin(pi*x/Lx);m2=-sin(pi*x/Lx);m3=0*y';m4=0*y';

A1=-2*eye(length(x))+diag(ones(1,length(x)-1),1)+diag(ones(1,length(x)-1),-1);

A2=-2*eye(length(y))+diag(ones(1,length(y)-1),1)+diag(ones(1,length(y)-1),-1);

dt=0.0001;

t=0:dt:1;

[Y,X]=meshgrid(y,x);%十分重要不同y构成行向量，不同x构成列向量

U0=exp(-10*((X-1/2).^2+(Y-1/2).^2));

U=U0;

e0=1;

for n=1:length(t)-1

    U=U+e0^2*(1/dx^2*A1*U+1/dy^2*U*A2)*dt;

    U(1,:)=m1*dy+U(2,:);

    U(end,:)=m2*dy+U(end-1,:);

    U(:,1)=m3*dx+U(:,2);

    U(:,end)=m4*dx+U(:,end-1);

    if mod(n,100)==1

    surf(X,Y,U)

    axis([x(1) x(end) y(1) y(end) -1 3])

    getframe;

    end

end

figure

[Ex,Ey]=gradient(-U,dx,dx);%求电场强度

contour(X,Y,U);%画等势线

hold on

quiver(X,Y,Ex,Ey);%画矢量

在matlab上运行得到图像：

发现电势未趋于稳定，而是一直升高，即没有解。

但热传导方程随时间演变要趋于0，在程序中我们只有输入的热量（边界只有正）因此不能得到静电场的结果。

因此将边界条件改为负号

m1=sin(pi*x/Lx);m2=-sin(pi*x/Lx);m3=0*y';m4=0*y';

这样之后才得到我们想要 的结果

1. 泊松方程

对泊松方程做体积分

有解条件很苛刻

视频讲解 

 

MATLAB教程——全站最适合理工类专业(求解拉普拉斯和泊松方程程序讲解)