版权声明:本文为原创文章:http://blog.csdn.net/programmer_wei/article/details/52072939
Logistic Regression(逻辑回归)是机器学习中一个非常非常常见的模型,在实际生产环境中也常常被使用,是一种经典的分类模型(不是回归模型)。本文主要介绍了Logistic Regression(逻辑回归)模型的原理以及参数估计、公式推导方法。
模型构建
在介绍Logistic Regression之前我们先简单说一下线性回归,,线性回归的主要思想就是通过历史数据拟合出一条直线,用这条直线对新的数据进行预测,线性回归可以参考我之前的一篇文章。
我们知道,线性回归的公式如下:
而对于Logistic Regression来说,其思想也是基于线性回归(Logistic Regression属于广义线性回归模型)。其公式如下:
其中,
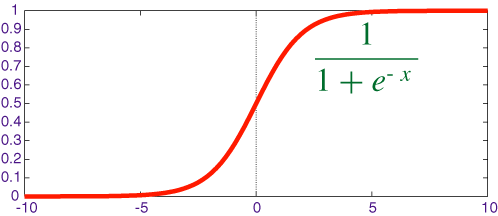
sigmoid的函数图形如下:
我们可以看到,sigmoid的函数输出是介于(0,1)之间的,中间值是0.5,于是之前的公式
hθ(x)
的含义就很好理解了,因为
hθ(x)
输出是介于(0,1)之间,也就表明了数据属于某一类别的概率,例如 :
hθ(x)
<0.5 则说明当前数据属于A类;
hθ(x)
>0.5 则说明当前数据属于B类。
所以我们可以将sigmoid函数看成样本数据的概率密度函数。
有了上面的公式,我们接下来需要做的就是怎样去估计参数 θ 了。
首先我们来看,
θ
函数的值有特殊的含义,它表示
hθ(x)
结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
极大似然估计
根据上式,接下来我们可以使用概率论中极大似然估计的方法去求解损失函数,首先得到概率函数为:
因为样本数据(m个)独立,所以它们的联合分布可以表示为各边际分布的乘积,取似然函数为:
取对数似然函数:
最大似然估计就是要求得使
l(θ)
取最大值时的
θ
,这里可以使用梯度上升法求解。我们稍微变换一下:
因为乘了一个负的系数 −1m ,然后就可以使用梯度下降算法进行参数求解了。梯度下降具体就不在这里多说了,可以参考之前的 文章。
参考文章:
http://blog.chinaunix.net/xmlrpc.php?r=blog/article&uid=9162199&id=4223505
http://blog.csdn.net/wangran51/article/details/8892923
























 4042
4042

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








