机器学习——逻辑回归（Logistic Regression）

一、理论

逻辑回归（Logistic Regression) 是一种广义的线性回归分析模型，它利用逻辑函数（通常是Sigmoid函数）将线性回归的输出值映射到0和1之间，从而用于处理二分类问题。

1.1 线性回归

1.1.1 线性回归的原理

线性回归是一种利用数理统计中回归分析的方法，来确定两种或两种以上变量间相互依赖的定量关系。其原理是假设因变量$Y$与自变量$X$之间存在线性关系，即$Y$可以表示为$X$的线性组合加上一个常数项。

1.1.2 线性回归的数学推导

1.1.2.1 模型设定

线性回归模型可以表示为：

$$Y=w_1{X}_1+w_2{X}_2+...+w_n{X}_n+b$$

其中:

1. $Y$是因变量；
2. $X_1,X_2,...,X_n$是自变量
3. $w_1,w_2,...,w_n$是回归系数
4. $b$是截距项

为了简化表示，我们可以引入一个额外的特征$X_0=1$，并将截距项$b$视为$w_0$，这样模型就可以表示为：

$$Y=w_0{X}_0+w_1{X}_1+w_2{X}_2+...+w_n{X}_n$$

进一步地，我们可以将上式写为矩阵形式：

$$Y={\mathbf{w}}^T\mathbf{X}$$

其中:

1. $\mathbf{w}=[w_0,w_1,w_2,...,w_n{]}^T$
2. $\mathbf{X}=[X_0,X_1,X_2,...,X_n{]}^T$

1.1.2.2 求解参数$\mathbf{w}$

从上述公式可以看出，线性回归模型的参数$\mathbf{w}$是我们要求解的，为了实现这个目标，我们进行以下操作。

1.1.2.2.1 损失函数

在线性回归中，我们通常使用均方误差（Mean Squared Error, MSE）作为损失函数，以衡量模型预测值与实际值之间的差异。损失函数的数学表达式为：

$$J(\mathbf{w})=\frac{1}{2m}\sum _{i=1}^m(y^{(i)}-{\mathbf{w}}^T{\mathbf{x}}^{(i)}{)}^2$$

其中:

1. $m$是样本数量
2. $y^{(i)}$是第$i$个样本的实际值
3. ${\mathbf{x}}^{(i)}$是第$i$个样本的特征向量。

1.1.2.2.2 优化算法

很显然，为了使模型能够契合某一个数据集，我们要使损失函数的值越小越好，而为了找到使损失函数最小的参数$\mathbf{w}$，我们通常采用梯度下降法（Gradient Descent） 进行求解。此外还有很多其它的优化算法，这边再介绍一个牛顿法（Newton’s Method）。

梯度下降法（Gradient Descent）

首先，我们需要计算损失函数 $J(\mathbf{w})$关于参数$\mathbf{w}$的梯度。

对于参数 $\mathbf{w}$的第 $j$个分量 $w_j$，其梯度为：

$$\frac{\partial J(\mathbf{w})}{\partial w_j}=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{w}}(x^{(i)})-y^{(i)})\cdot \frac{\partial }{\partial w_j}({\mathbf{w}}^T{\mathbf{x}}^{(i)})$$

由于
$${\mathbf{w}}^T{\mathbf{x}}^{(i)}=\sum _{k=1}^n{w}_k{x}_k^{(i)}$$

其中:

1. $n$是特征数量

所以：

$$\frac{\partial }{\partial w_j}({\mathbf{w}}^T{\mathbf{x}}^{(i)})=x_j^{(i)}$$

因此，梯度为：

$$\nabla J(\mathbf{w})=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{w}}(x^{(i)})-y^{(i)}){\mathbf{x}}^{(i)}$$

梯度下降法的参数更新公式为：

$$\mathbf{w}:=\mathbf{w}-\alpha \nabla J(\mathbf{w})$$
其中 :

1. $\alpha$是学习率。

牛顿法（Newton’s Method）

牛顿法是一种二阶优化方法，它使用损失函数的二阶导数（Hessian矩阵）来加速收敛。

首先，我们需要计算$J(\mathbf{w})$的Hessian矩阵 $H$，其元素为：

$$H_{jk}=\frac{{\partial }^{2}J(\mathbf{w})}{\partial w_j\partial w_k}=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{w}}(x^{(i)})-y^{(i)}){\left(\frac{\partial }{\partial w_j}{\mathbf{x}}^{(i)}\right)}^T\left(\frac{\partial }{\partial w_k}{\mathbf{x}}^{(i)}\right)+\frac{1}{m}\sum _{i=1}^m{\mathbf{x}}_j^{(i)}{\mathbf{x}}_k^{(i)}$$
由于
$$\frac{\partial }{\partial w_j}{\mathbf{x}}^{(i)}={\mathbf{e}}_j$$
其中：

1. $(e{)}_j$是第 $j$个分量为 1，其余为 0 的单位向量

所以：

$$H_{jk}=\frac{1}{m}\sum _{i=1}^m(h_{\mathbf{w}}(x^{(i)})-y^{(i)})x_j^{(i)}{x}_k^{(i)}+\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}{x}_k^{(i)}$$

牛顿法的参数更新公式为：

$$\mathbf{w}:=\mathbf{w}-H^{-1}\nabla J(\mathbf{w})$$

其中 ：

1. $H^{-1}$是Hessian矩阵的逆。

1.1.2.2.3 两个优化算法的对比

梯度下降法是一种简单而有效的优化算法，适用于各种规模的数据集。然而，它对于学习率的选择比较敏感，且通常需要多次迭代才能达到最优解。
牛顿法 具有二阶收敛性，通常比梯度下降法更快达到最优解。但是，它需要计算目标函数的二阶导数（Hessian矩阵），这在大规模数据集上可能非常耗时。此外，如果Hessian矩阵不正定，牛顿法可能无法收敛到最优解。

1.2 Sigmoid函数

在逻辑回归中，当我们已经有了线性回归模型的基础后，为了将模型的输出转换为概率值（即预测某个事件发生的可能性），我们引入了sigmoid函数。

1.2.1 Sigmoid函数的原理

Sigmoid函数（也称为逻辑函数或S型函数）是一种可以将任何实数映射到0和1之间的函数。在逻辑回归中，这个函数的主要目的是将线性模型的输出转换为一个介于0和1之间的概率值，这样我们就可以用这个概率值来判断某个样本属于正类（例如，标签为1）的概率。

1.2.2 数学公式解释

Sigmoid函数的数学公式为：

$$\sigma (z)=\frac{1}{1+e^{-z}}$$

其中:

1. $z$ 是线性模型的输出，即 $z={\theta }^{T}x$
2. $\theta$ 是参数向量，$x$是特征向量

以下是sigmoid函数展示的python代码和sigmoid函数图

import numpy as np
import matplotlib.pyplot as plt

# 定义sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 创建一个z值的范围
z = np.linspace(-10, 10, 500)  # 从-10到10，总共500个点

# 计算对应的sigmoid值
sigmoid_values = sigmoid(z)

# 绘制图像
plt.plot(z, sigmoid_values, label='Sigmoid Function')

# 添加标题和标签
plt.title('Sigmoid Function')
plt.xlabel('z')
plt.ylabel('σ(z)')

# 显示图例
plt.legend()

# 显示图像
plt.grid(True)
plt.show()

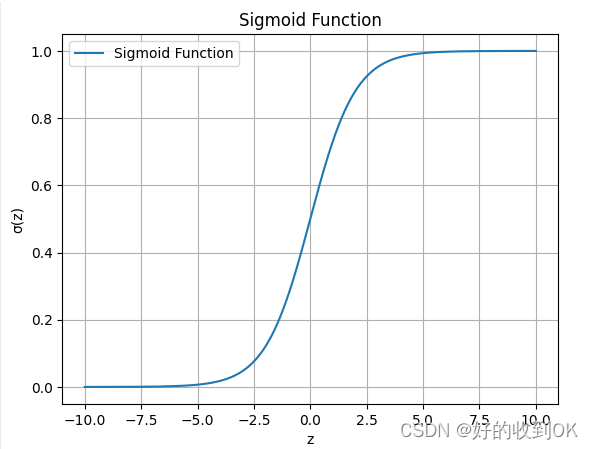
Sigmoid函数特性

1. 当$z$ 趋于正无穷时，$e^{-z}$趋于0，因此$\sigma (z)$ 趋于1。
2. 当$z$ 趋于负无穷时，$e^{-z}$趋于正无穷，但 $1+e^{-z}$也趋于正无穷，因此 $\sigma (z)$趋于0。
3. 当$z=0$时，$\sigma (z)=0.5$。

这些性质使得sigmoid函数非常适合作为逻辑回归的输出函数，因为它可以将任意实数映射到0和1之间的概率值。

1.3 逻辑回归

1.3.1 逻辑回归的概念

逻辑回归（Logistic Regression）是一种用于处理二分类问题的统计学习方法，它通过Sigmoid函数将线性模型的输出转化为概率值，从而预测分类结果。

1.3.2 逻辑回归的原理

逻辑回归的原理是假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降等优化算法，估计出参数的值。其输出值始终在0和1之间，是一个概率值，表示样本为正例的可能性。

1.3.3 逻辑回归的数学推导

1.3.3.1Sigmoid函数

逻辑回归中，我们使用Sigmoid函数（有时也称为逻辑函数）将线性模型的输出转换为概率值。Sigmoid函数的数学形式为：

$$g(z)=\frac{1}{1+e^{-z}}$$

其中:

1. $z={\theta }^{T}X$，$\theta$是参数向量
2. $X$是特征向量

1.3.3.2 预测函数（或称为条件概率）

逻辑回归的预测函数表示样本为正例的概率，数学表达式为：

$$h_{\theta }(x)=P(y=1|x;\theta )=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

同样地，样本为负例的概率为：

$$P(y=0|x;\theta )=1-h_{\theta }(x)$$

1.3.3.3 似然函数

对于给定的数据集，我们希望找到一组参数 $\theta$，使得这组参数下所有样本被正确分类的概率最大。这可以通过最大化似然函数来实现。似然函数的数学形式为：

$$L(\theta )=\prod _{i=1}^{m}P(y_i|x_i;\theta )$$

其中：

1. $m$ 是样本数量
2. $y_i$是第$i$ 个样本的真实标签
3. $x_i$是第 $i$ 个样本的特征向量

将 $h_{\theta }(x)$ 的表达式代入似然函数中，得到：

$$L(\theta )=\prod _{i=1}^m[h_{\theta }(x_i){]}^{y_i}[1-h_{\theta }(x_i){]}^{1-y_i}$$

1.3.3.4 对数似然函数

由于直接对似然函数进行优化较为困难，我们通常取对数似然函数进行优化。对数似然函数的数学形式为：

$$l(\theta )=\log L(\theta )=\sum _{i=1}^m[y_i\log h_{\theta }(x_i)+(1-y_i)\log (1-h_{\theta }(x_i))]$$

1.3.3.5 梯度下降

为了找到使对数似然函数最大的参数 $\theta$，我们可以使用梯度下降等优化算法。梯度下降算法通过迭代更新参数 $\theta$来最小化损失函数（这里的损失函数为 $-l(\theta )$）。

梯度下降算法的参数更新公式为：

$${\theta }_j:={\theta }_j-\alpha \frac{\partial (-l(\theta ))}{\partial {\theta }_j}$$

其中:

1. $\alpha$是学习率，控制参数更新的步长。

对 $-l(\theta )$求偏导，得到：

$$\frac{\partial (-l(\theta ))}{\partial {\theta }_j}=-\sum _{i=1}^m[y_i\frac{1}{h_{\theta }(x_i)}\frac{\partial h_{\theta }(x_i)}{\partial {\theta }_j}-(1-y_i)\frac{1}{1-h_{\theta }(x_i)}\frac{\partial h_{\theta }(x_i)}{\partial {\theta }_j}]$$

由于
$$h_{\theta }(x_i)=g({\theta }^T{x}_i)$$

根据链式法则，我们可以进一步计算 $\frac{\partial h_{\theta }(x_i)}{\partial {\theta }_j}$：

$$\frac{\partial h_{\theta }(x_i)}{\partial {\theta }_j}=\frac{\partial g({\theta }^T{x}_i)}{\partial {\theta }_j}=g({\theta }^T{x}_i)(1-g({\theta }^T{x}_i))x_i^j$$

将上述结果代入梯度下降的参数更新公式中，即可迭代更新参数 $\theta$，直到满足收敛条件。

1.3.4 逻辑回归的算法流程

算法过程主要包括以下几个步骤：

1. 初始化参数$\theta$（可以随机初始化或设为零向量）。
2. 计算当前参数下每个样本的预测概率$h_{\theta }(x_i)$。
3. 根据预测概率和真实标签计算对数似然函数的值$l(\theta )$。
4. 计算对数似然函数对参数$\theta$ 的梯度 $\frac{\partial (-l(\theta ))}{\partial {\theta }_j}$。
5. 使用梯度下降算法更新参数$\theta$。
6. 重复步骤2-5，直到满足收敛条件（如损失函数值的变化小于某个阈值，或达到最大迭代次数等）。

1.3.5 正则化

正则化是一种防止过拟合的有效方法，它通过向目标函数中添加一个与模型参数相关的惩罚项来实现。L1正则化和L2正则化是两种常用的正则化方法，它们分别假设模型参数服从拉普拉斯分布和高斯分布。通过调整正则化参数，我们可以控制正则化的强度，从而平衡模型的复杂性和泛化能力。

1.3.5.1 正则化的数学原理

正则化的数学原理可以概括为通过向目标函数（如损失函数）中添加一个惩罚项来防止过拟合。这个惩罚项通常与模型的参数（如权重）的某种范数（如L1范数或L2范数）相关。正则化的目的是限制模型参数的数值范围，使得模型更加稳定，并且避免对训练数据的过度依赖。

引入先验信息

从贝叶斯理论的角度来看，正则化是人为引入先验信息的过程。通过假设模型参数服从某种先验分布（如拉普拉斯分布或高斯分布），我们可以将正则化项视为这种先验分布的负对数似然。这样，正则化就可以被解释为一种在训练过程中不断修正先验分布的过程。

限定参数范围

正则化的直接作用是限定参数的数值范围。通过添加正则化项，我们可以使得模型的参数值更加接近0（对于L1正则化）或更加平滑（对于L2正则化）。这有助于减少模型对特定特征的依赖，提高模型的泛化能力。

奥卡姆剃刀原理

正则化也符合奥卡姆剃刀原理，即“如无必要，勿增实体”。通过限制模型参数的复杂性（即减少参数的数量或限制参数的范围），我们可以使得模型更加简单，从而避免过拟合。

1.3.5.2 正则化公式推导

L1正则化

L1正则化假设模型参数服从拉普拉斯分布。其公式可以表示为：

$$J_{\text{L1}}(\theta ;X,y)=J(\theta ;X,y)+\alpha \sum _{i=1}^n|w_i|$$

其中：

1. $J(\theta ;X,y)$是原始的目标函数（如损失函数）
2. $\alpha$是正则化参数（控制正则化的强度）
3. $w_i$是模型的参数（如权重）

L2正则化

L2正则化假设模型参数服从高斯分布。其公式可以表示为：

$$J_{\text{L2}}(\theta ;X,y)=J(\theta ;X,y)+\frac{\alpha }{2}\sum _{i=1}^n{w}_i^2$$

其中：

1. $J(\theta ;X,y)$是原始的目标函数
2. $\alpha$是正则化参数
3. $w_i$是模型的参数

1.3.6 逻辑回归的优缺点

优点

1. 解释性强：逻辑回归的输出结果易于理解，可以明确地看到各个特征对结果的影响。
2. 计算效率高：逻辑回归的计算相对简单，计算成本较低，特别是当特征维度较高时，依然能够保持较快的计算速度。
3. 易于实现：逻辑回归模型简单，易于编程实现，并且有许多现成的库（如scikit-learn）可以直接使用。
4. 适用于二分类问题：逻辑回归模型适用于解决二分类问题，是二分类问题的常用方法之一。
5. 稳健性：逻辑回归对于特征工程的要求不是特别高，不太容易受异常值的影响，较为稳健。

缺点

1. 对非线性问题处理不佳：逻辑回归假设输入特征和输出之间是线性关系，对于非线性问题，逻辑回归可能无法很好地拟合数据。
2. 对多重共线性敏感：当特征之间存在多重共线性（即特征之间高度相关）时，逻辑回归的性能可能会受到影响。
3. 容易欠拟合：由于逻辑回归模型简单，其拟合能力有限，当数据复杂度高或存在大量噪声时，逻辑回归容易欠拟合。
4. 对异常值敏感：虽然逻辑回归相对于某些模型来说较为稳健，但当数据中存在极端异常值时，其性能还是可能会受到影响。
5. 不适用于多分类问题：虽然可以通过一些方法（如一对多、多对多等）将逻辑回归应用于多分类问题，但其本质上还是为二分类问题设计的，对于多分类问题可能不是最佳选择。

1.3.7 逻辑回归的应用场景

1. 二分类问题：逻辑回归是二分类问题的常用算法，如邮件是否为垃圾邮件、用户是否会点击某个广告、肿瘤是否为恶性等。

2. 风险评估：在金融领域，逻辑回归可用于评估贷款违约风险、信用评分等。通过客户的历史数据，可以预测他们未来是否可能违约。

3. 疾病预测：在医疗领域，逻辑回归可用于预测某种疾病的发生概率，如根据患者的病史、症状等信息预测是否患有某种疾病。

4. 市场营销：在市场营销中，逻辑回归可用于预测客户对产品的购买意愿、对促销活动的响应等，从而帮助制定更精准的市场策略。

5. 文本分类：在文本挖掘和自然语言处理中，逻辑回归可用于文本分类任务，如情感分析（正面/负面评价）、主题分类等。

6. 电子商务：在电子商务领域，逻辑回归可用于预测用户是否会购买某个商品、是否会再次访问网站等，从而优化用户体验和增加销售额。

7. 社会科学：在社会科学研究中，逻辑回归可用于分析各种因素（如年龄、性别、教育水平等）对某个社会现象（如投票意向、满意度等）的影响。

二、代码实现

2.1 导入库

导入所需的库

# 导入库
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, precision_recall_curve, auc
import matplotlib.pyplot as plt

2.2 数据准备和划分

逻辑回归是一个二分类算法，所以这里使用了乳腺癌数据集，导入数据集之后，对数据集进行划分。

# 加载数据集
cancer = load_breast_cancer()
X = cancer.data
y = cancer.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

2.3 添加偏置项

这里，np.ones((X_train.shape[0], 1)) 创建了一个形状为 (n_samples, 1) 的数组，其中 n_samples 是 X_train 的样本数量，所有元素的值都是1。np.hstack 函数用于水平堆叠两个数组，即将这个全1的数组添加到 X_train 的最前面。这样做的目的是为模型添加一个偏置项（或截距项），它表示当所有特征都为0时，模型的预测值是多少。对于测试集 X_test，也进行了相同的操作。

# 添加偏置项
X_train = np.hstack((np.ones((X_train.shape[0], 1)), X_train))
X_test = np.hstack((np.ones((X_test.shape[0], 1)), X_test))

2.4 初始化参数

n_features：获取了X_train的特征数量（现在包括了我们刚刚添加的偏置项）。然后，我们创建了一个与特征数量相同长度的零向量theta。这个 theta实际上是我们模型的参数，对于线性回归，它表示每个特征的权重以及偏置项。
learning_rate：这是梯度下降等优化算法的学习率，它决定了参数在每次迭代时更新的步长。较大的学习率可能导致训练不稳定，而较小的学习率可能导致训练速度过慢。
reg_param： 这是正则化参数，用于防止模型过拟合。在训练过程中，正则化项会将 theta 的大小（或L2范数）作为惩罚项加入到损失函数中。较大的正则化参数会导致模型更简单，可能降低其在测试集上的性能，但有助于防止过拟合。
epochs ：表示训练过程中将完整数据集通过模型多少次。在每次 epoch 中，模型都会看到整个数据集，并使用梯度下降或其他优化算法来更新其参数。较大的 epochs 值可能导致模型在训练集上表现更好，但也可能导致过拟合。

# 初始化参数
n_features = X_train.shape[1]
theta = np.zeros(n_features)

# 学习率和正则化参数
learning_rate = 0.01
reg_param = 0.1
epochs = 1000

2.4 逻辑回归的函数

2.4.1 Sigmoid函数

为了限制z的最大值和最小值以避免数值溢出，这边选定了-700，700作为界限。

def sigmoid(z):
    z = np.clip(z,-700,700)
    return 1 / (1 + np.exp(-z))

2.4.2 逻辑回归模型

用一个函数来进行逻辑回归的线性预测和激活函数sigmoid函数的计算。这里使用了 NumPy 的 dot 函数来计算 X 和 theta 的点积，即线性预测。最终返回每个样本属于正例的值。

# 逻辑回归模型
def logistic_regression(X, theta):
    z = np.dot(X, theta)
    return sigmoid(z)

2.4.3 损失函数

compute_cost函数是用来计算逻辑回归模型的损失函数（也称为成本函数），并且它包含了L2正则化项。

1. 首先通过y的长度获取样本数量m。然后调用logistic_regression函数来计算预测概率h，它对应于样本属于正类的概率。
2. 接着计算未正则化的损失cost，这是逻辑回归的损失函数（交叉熵损失），其中加上了1e-15是为了防止在计算对数时发生数值不稳定性（例如，当h或1-h接近0时）。这个损失函数衡量了模型预测与真实标签之间的差异。
3. 再然后计算L2正则化项用于防止模型过拟合。这里只对theta中的特征权重（不包括偏置项theta[0]）进行正则化。np.square(theta[1:])计算了从第二个元素开始的所有元素的平方，然后求和。乘以(reg_param / (2 * m))是为了得到正则化项的值。
4. 最后返回总损失，将未正则化的损失cost和正则化项reg_term相加，得到总损失。这个总损失将用于后续的模型训练过程（例如，在梯度下降算法中用于更新theta）。

# 损失函数（包括L2正则化）
def compute_cost(X, y, theta, reg_param):
    m = len(y)
    h = logistic_regression(X, theta)
    cost = (-1 / m) * np.sum(y * np.log(h + 1e-15) + (1 - y) * np.log(1 - h + 1e-15))
    reg_term = (reg_param / (2 * m)) * np.sum(np.square(theta[1:]))  # 不对偏置项进行正则化
    return cost + reg_term

2.4.4 梯度下降

gradient_descent函数是用于实现逻辑回归的梯度下降算法。

1. 首先进行初始化，m代表样本数量，即y的长度，cost_history代表一个长度为epochs的数组，用于存储每次迭代的成本值。
2. 然后进行梯度下降循环，对于每一个迭代it（从0到epochs-1）使用当前的theta和X计算逻辑回归的假设值h，计算预测值h与目标值y之间的误差error。
3. 接着计算梯度grad，通过X的转置和误差的乘积然后除以m来完成。
4. 再然后计算正则化梯度reg_grad，这里只对theta的非偏置项（即除了第一个元素以外的所有元素）进行正则化。再将正则化梯度加到原始的梯度上（只针对非偏置项）。
5. 接着更新theta，通过从theta中减去学习率乘以梯度来实现。
6. 最后计算当前的成本值并存储在cost_history的相应位置，返回更新后的theta和cost_history。

# 梯度下降
def gradient_descent(X, y, theta, learning_rate, reg_param, epochs):
    m = len(y)
    cost_history = np.zeros(epochs)

    for it in range(epochs):
        h = logistic_regression(X, theta)
        error = h - y
        grad = (1 / m) * np.dot(X.T, error)
        reg_grad = (reg_param / m) * theta[1:]  # 不对偏置项进行正则化
        grad[1:] += reg_grad
        theta -= learning_rate * grad
        cost_history[it] = compute_cost(X, y, theta, reg_param)

    return theta, cost_history

2.4 训练模型

先将训练集传入训练模型进行训练，然后将测试集进行预测，将预测概率转换为二分类的预测标签。

# 训练模型
theta, cost_history = gradient_descent(X_train, y_train, theta, learning_rate, reg_param, epochs)

# 预测概率
y_pred_prob = logistic_regression(X_test, theta)

# 将预测概率转换为预测标签（假设概率大于0.5为1，否则为0）
y_pred = (y_pred_prob > 0.5).astype(int)

2.5 评估模型

最后将训练的模型进行评估，这里评估了准确率，绘制了损失曲线、ROC曲线和PR曲线。

# 计算准确率
accuracy = np.mean(y_pred == y_test)
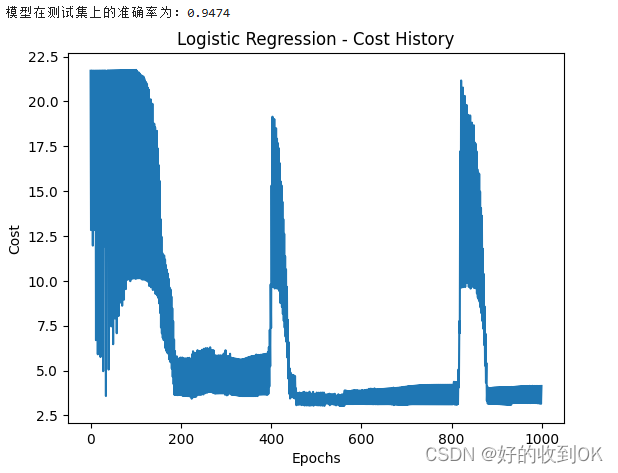
print(f"模型在测试集上的准确率为：{accuracy:.4f}")

# 绘制损失曲线
plt.plot(cost_history)
plt.xlabel('Epochs')
plt.ylabel('Cost')
plt.title('Logistic Regression - Cost History')
plt.show()

# 绘制ROC曲线
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], 'k--', label='Random Guess')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()

# 绘制PR曲线
precision, recall, _ = precision_recall_curve(y_test, y_pred_prob)
pr_auc = auc(recall, precision)
plt.figure(figsize=(10, 6))
plt.plot(recall, precision,label=f'PR curve (area = {pr_auc:.2f})')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curves')
plt.legend(loc="lower left")
plt.show()

三、结果分析

3.1 结果展示

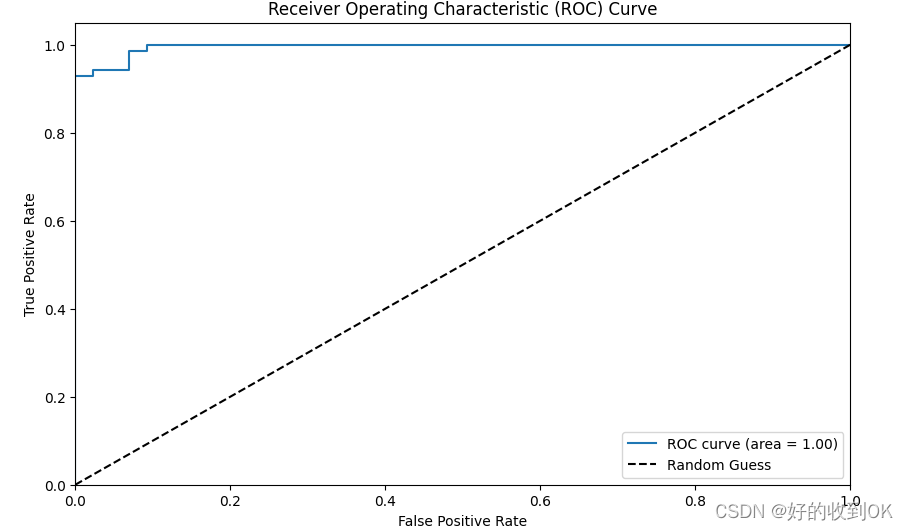
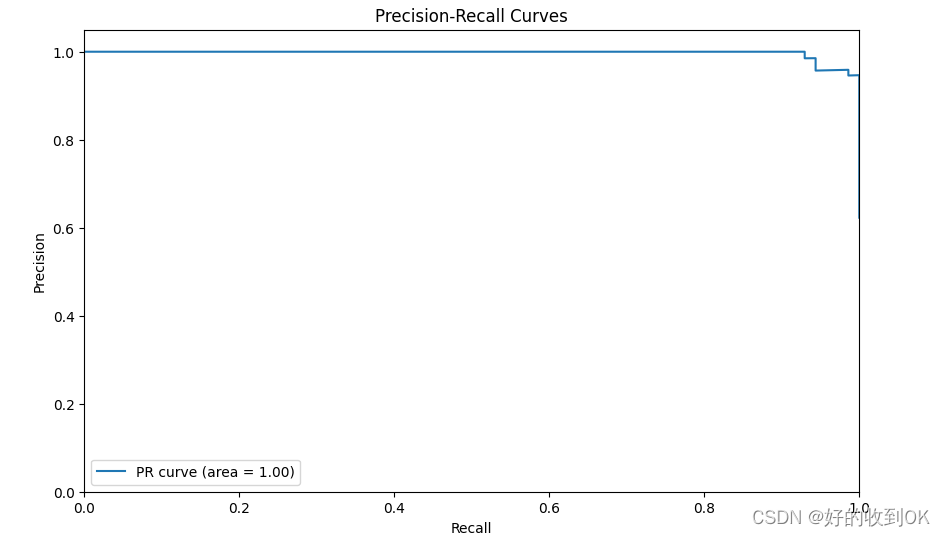
以下是准确率、损失曲线、ROC曲线、PR曲线结果图。

3.2 结果分析

1. 首先，从“Logistic Regression - Cost History”图表中可以看到，模型在训练过程中随着训练次数epochs的增加，训练集的损失逐渐减小，这说明模型正在逐渐学习到数据中的特征并优化其性能。而验证集的损失保持相对稳定，并且没有明显的上升趋势，这表明模型没有过拟合，具有良好的泛化能力。
2. 其次，模型在测试集上的准确率为0.9474，这是一个相当高的准确率，说明模型在实际应用中具有较好的表现，能够有效地对数据进行分类或预测。
3. 再者，通过比较训练集和验证集的损失曲线，可以看出模型在训练集上的性能提升并没有导致验证集上的性能下降，这进一步证明了模型的稳定性和有效性。
4. 接着，从其ROC曲线也能看出，分类性能很好。ROC曲线几乎紧贴左上角，这意味着在假阳性率（FPR）很低的情况下，真阳性率（TPR）也很高。这表明所使用的分类器性能非常好，能够有效地识别正样本同时减少负样本的误报。
5. 最后，从PR曲线也能看出，曲线从左上方开始，表示当分类器非常保守，几乎只识别确定为正例的样本时（精确度为1.00），它只能识别出一小部分真正的正例（召回率较低）。随着曲线向右下方延伸，精确度逐渐下降，但召回率逐渐增加，表示分类器开始降低阈值，以便识别更多的正例，但这样做也增加了误报（即将负例错误地识别为正例）的可能性。当精确度为0.8时，召回率也达到了0.8，这意味着分类器在降低一部分精确度的同时，能够识别出80%的真正正例。整个PR曲线下的面积（AUC-PR）为1.00，这是理想的情况，表明分类器在所有阈值下都能达到最佳的精确度和召回率之间的平衡。

总的来说，这个实验结果表明所训练的逻辑回归模型具有良好的性能和泛化能力，能够在不同数据集上实现较高的准确率。同时，模型在训练过程中没有出现过拟合现象，说明模型的参数设置和训练策略是有效的。