线性代数基础9--正交矩阵与行列式基础,代数余子式

最新推荐文章于 2023-08-23 11:23:07 发布
最新推荐文章于 2023-08-23 11:23:07 发布
阅读量3.4k 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： 基础 文章标签： 线性代数 矩阵 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/pu_pupupupupu/article/details/122520928

1,正交基与正交矩阵
标准正交向量组中,向量之间满足两两正交,并且每个基的长度为1
在这里插入图片描述
将标准正交向量组成一个矩阵Q.则有一个重要的性质,并且不要求Q一定为方阵.如下
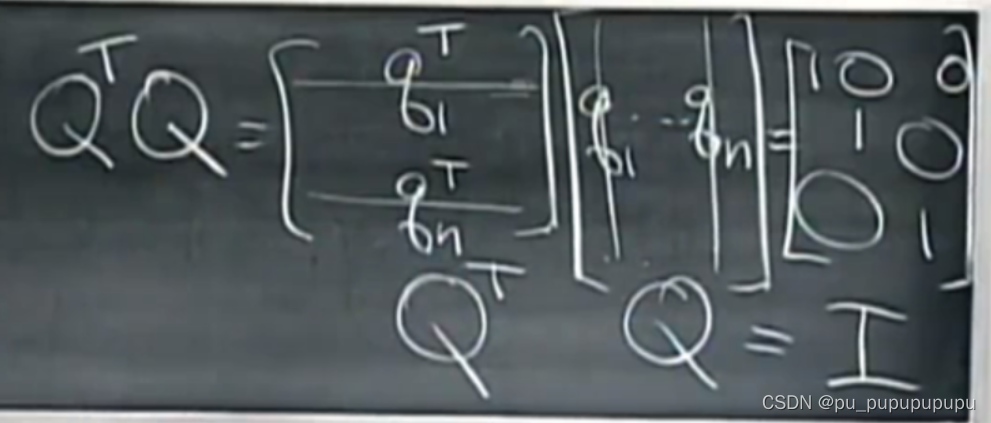
在这里插入图片描述
这里我们将标准正交矩阵,并且只有在Q为方阵的情况下才,简称为正交矩阵.
强调方阵是因为可逆
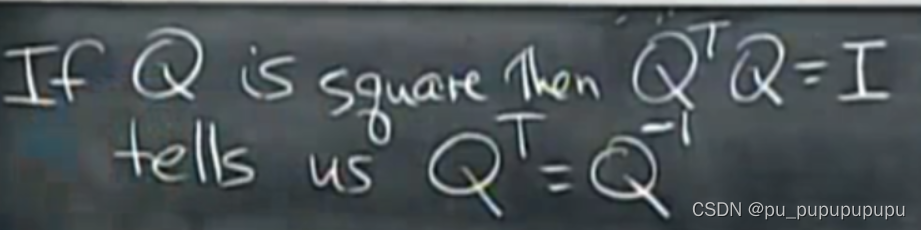
在这里插入图片描述
也许有一个问题是正交矩阵是否可逆,但是正交矩阵符合可逆的定义,我们还找出了它的可逆矩阵,(如果这两个矩阵乘积为单位矩阵,并且是方阵,那么它们互为可逆),所以Q一定可逆,也就可以说明,正交向量一定线性无关.是可以证明的,有兴趣可以网上查看.也可以简单的从正交向量几何意义解释,两个向量垂直当然除了0没有组合可以让其结果为0向量

这里有一个注意的点,一般只有方阵才考虑逆矩阵

Q的例子
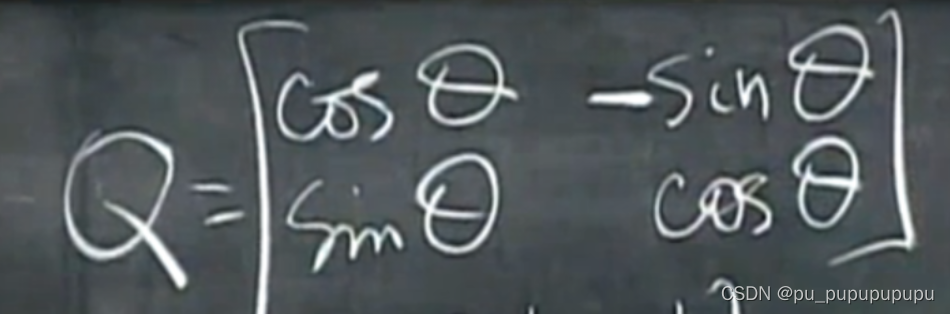
在这里插入图片描述
在这里插入图片描述

最低0.47元/天 解锁文章

200万优质内容无限畅学
计算正交矩阵的行列式
DevEnigma的博客
08-26 1036
正交矩阵是一种非常重要的矩阵类型，在许多数学和工程应用中起着关键的作用。在本文中，我们将讨论如何使用C++编写代码来计算正交矩阵的行列式。最后，我们将矩阵对角线上的元素相乘，得到最终的行列式值。如果输入矩阵不是方阵，或者不满足正交矩阵的定义条件，结果将是不可预测的。希望本文提供的代码和解释对你有所帮助，让你能够理解如何计算正交矩阵的行列式。首先，让我们明确正交矩阵的定义。现在，让我们开始编写计算正交矩阵行列式的代码。的函数，用于计算给定矩阵的行列式。函数中，我们创建了一个3×3的示例正交矩阵，并调用。
【数学二】线性代数-矩阵-伴随矩阵、可逆矩阵
最新发布
WEL测试
11-03 299
【数学二】线性代数-矩阵-伴随矩阵、可逆矩阵
矩阵知识：正交矩阵、行列式、子式与代数余子式
kking_edc的博客
06-09 6592
一、正交矩阵 1.1 RnR^nRn的标准正交基 1.1.1 定义1 Rn中的n个向量η1,η2,...,ηn满足:R^n中的n个向量\eta_1,\eta_2,...,\eta_n满足:Rn中的n个向量η1​,η2​,...,ηn​满足: (1)两两正交：ηiTηj=0(i≠0)(1)两两正交：\eta_i^T\eta_j=0(i\ne0)(1)两两正交：ηiT​ηj​=0(i​=0) (2)都是单位向量，即∣∣ηi∣∣=1,i=1,2,...,n(2)都是单位向量，即||\eta_i||=1,i=1,
矩阵的秩，行列式，代数余子式啥的
ezoileaner的博客
10-17 3595
参考资料: nealchen Rose_max 求解A的代数余子式: (1)rank(A)<=n-2，每个位置均为0 (2)rank(A)=n,有A∗=∣A∣∗A−1A^*=|A|*A^{-1}A∗=∣A∣∗A−1,其中A*是代数余子式矩阵的转置矩阵，实现的时候需要注意这点 (3)rank(A)=n-1,则求出非0行向量p,满足pA=0，以及非0列向量q,满足Aq=0 找出一对r,c，满足pr≠0,qc≠0p_r\neq 0,q_c\neq 0pr​​=0,qc​​=0，我们有Ai,j=piqjp
主子式、顺序主子式、余子式、代数余子式
SL_World的博客
04-06 4113
原文出处： ① https://blog.csdn.net/yskyskyer123/article/details/87891051 ② https://blog.csdn.net/qq_34824576/article/details/102678671
线性代数基础10--特征值与特征向量,行列式的空间关系
pu_pupupupupu的博客
01-17 2832
1,逆矩阵公式 对于n阶矩阵来说,逆可以这样求出来,其中C矩阵为对应元素代数余子式组成的矩阵,C的转置就是我们熟悉的伴随矩阵.也可以用来求A的逆. 那么为什么会这样呢?我们应该证明这个公式 首先,如果一个元素来自某一行,但是它×另一行元素的对应列数的代数余子式那么结果为0.如上图中第一行[a,b]×第二列[-b,a]=0 为什么这样呢?简单的理解就是,第i行的元素分别乘以对应的第j行元素的代数余子式，就相当于把原行列式的第j行元素替换成第i行元素，再按第j行展开。那么第i行与第j行是相同的,行列式也就为0
矩阵-线性代数-基础.pdf
05-04
伴随矩阵是由原矩阵的代数余子式构成的，它与原矩阵的乘积等于矩阵的行列式乘以单位矩阵。伴随矩阵也与共轭转置变换有关，共轭转置是指先转置后对每个元素取共轭，即Hermite共轭变换。 矩阵的秩是指矩阵中线性独立...
线性代数基础知识点回顾与总结（一）：行列式与矩阵
qq_29700227的博客
03-06 3784
** 一：行列式 ** 排列： 1，2,···，n组成的有序数组称为n阶排列。 逆序：大数排在小数前。自然排列为偶排列。 n阶行列式的值等于不同行的n个元素的乘积的代数和： 注 ：主对角元素减副对角元素的求法只适用于2或3阶行列式的计算中。 三角行列的值： 注：副主对角时要考虑正负号： 方阵行列式（n*n）:  ∣AB∣=∣A∣⋅∣B∣;∣A2∣=∣A∣2 .\ |AB|=|A|·|B|; |A^{2}|=|A|^{2}\,.  ∣AB∣=∣A∣⋅∣B∣;∣A2∣=∣A∣2. 行
行列式的子式、主子式、顺序主子式、余子式、代数余子式
hyl1181的博客
12-13 4万+
k阶子式：指在行列式中任取k行k列组成的行列式。k行k列是任意组合没有限定要求，只要行列相等即可。 k阶主子式：指在行列式中选k行k列，但要求行和列的下标相同。如：行为r1、r2、r3，列必须为c1、c2、c3；行为r2、r3、r5，列必须为c2、c3、c5。因此，k阶主子式不唯一。 k阶顺序主子式：指在行列式中选k行k列，但要求下标只能从1行、1列依次按顺序选取，即选取前k行和前k列，保证满足若rs行在，那么rs-1行也在。因此，顺序主子式是唯一的。 余子式：在n阶行列式中，去掉aij所在的ri行与cj列
线性代数的学习和整理11: 子式与余子式
奔跑的犀牛先生
08-23 2万+
$\left[\right]$$
常见的几类矩阵（正交矩阵、酉矩阵、正规矩阵等）
热门推荐
lch的博客
07-27 7万+
目录实对称矩阵定义实反对称矩阵定义厄米特矩阵定义反厄米特矩阵定义正交矩阵定义性质酉矩阵（幺正矩阵）定义性质正规矩阵定义性质正定矩阵定义性质充要条件友矩阵（伴侣矩阵）定义性质旋转矩阵定义性质对比 实对称矩阵 定义 AT=AA^T=AAT=A 实反对称矩阵 定义 AT=−AA^T=-AAT=−A 厄米特矩阵 定义 AH=AA^H=AAH=A 反厄米特矩阵 定义 AH=−AA^H=-AAH=−A 正交矩阵 定义 ATA=AAT=IA^TA=AA^T=IATA=AAT=I 换言之，当AT=A−1A^T=A
【线性代数公开课MIT Linear Algebra】 第十七课 正交基和正交矩阵
weixin_30561177的博客
11-08 402
本系列笔记为方便日后自己查阅而写，更多的是个人见解，也算一种学习的复习与总结，望善始善终吧~ 1. 标准正交基与正交矩阵 标准正交向量组 orthonomal vectors 彼此正交orthogonal且模长norm为1(normalized) 当做column vecor写成矩阵形式： 对于这样的矩阵，我们理所当然的要去观察他的QTQ 这个式...
线性代数学习笔记5-3：标准正交基、正交矩阵、施密特正交化、QR分解
Insomnia_X的博客
08-07 3304
将一组标准正交向量作为列向量，得到的矩阵为Q\mathbf QQ 根据上面的性质，这个矩阵一定满足QTQ=[q1Tq2Tq3T][q1q2q3]=I\mathbf Q^T\mathbf Q=\begin{bmatrix}q_1^T\\q_2^T\\q_3^T\end{bmatrix}\begin{bmatrix}q_1&q_2&q_3\end{bmatrix}=\mathbf IQTQ=⎣⎡​q1T​q2T​q3T​​⎦⎤​[q1​​q2​​q3​​]=I（但是QTQ≠I\mathbf Q^T\mathbf
正交矩阵
weixin_43233770的博客
10-13 9510
正交矩阵
正交矩阵及其性质
thompson的博客
11-04 8051
摘自《高等代数(上)》丘维声, p144
线性代数（9）：线性正交
jc15274630894的博客
07-09 3万+
线性代数（9）
线性代数知识点总结
weixin_62999028的博客
06-08 7560
（2）若n维列向量α1，α2，α3 线性无关，β1，β2，β3 可以由其线性表示，即（β1，β2，β3）=（α1，α2，α3）C，则r（β1，β2，β3）=r（C），从而线性无关。，αn 与β1，β2，…（4）当r（A）=1，即A=αβT，其中α，β均为n维非零列向量，则A的特征值为λ1=Σaii=αTβ=βTα，λ2=…（2）设A是m×n阶矩阵，r（A）=n，B是n×s阶矩阵，则齐次方程ABx=0与Bx=0同解，r（AB）=r（B），αs线性无关，α1，α2，…，αs，β线性相关，则β可由α1，α2，…
正交矩阵的定义及证明和性质
linux-0.11调试教程
03-21 4万+
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值