一. 数列
数列是特殊的序列,全部由数字组成。
1.1 通项公式 与 有通项公式的数列
如果存在某种以正整数为定义域的函数, 使得数列每一项的 标号 和数列每一项的值满足某种关系。
则这个函数被称为这个数列的 通项公式.
且通项公式足以描述整个数列.
eg: 1, 1/2, 1/3 ... 1/x
其通项公式为
f
(
x
)
=
1
x
f(x) = \frac{1}{x}
f(x)=x1
其定义域,也就是数列的标号范围为:
x
∈
(
0
,
+
∞
)
x \in (0, +\infty)
x∈(0,+∞)
1.2 数列通项公式的另一种表达形式
这种表达方式可能会使人困惑(x 会被联想为函数中的因变量,其实不是)
eg: 1, 1/2, 1/3 ... 1/n
通项公式:
x
n
x_n
xn
其中, x 代表函数名, n 代表函数因变量.
x
n
x_n
xn 的本质为函数:
x
(
n
)
=
1
n
x(n) = \frac{1}{n}
x(n)=n1,
n
∈
(
0
,
+
∞
)
n \in (0, +\infty)
n∈(0,+∞)
1.3 关于数列通项公式的定义域解释
接下来我们以 x n x_n xn 来表达数列的通项
谨记, x n x_n xn 是一个函数.
n 不能取 0, 因为规定。
n 不能取
+
∞
+\infty
+∞,
- 因为 + ∞ \infty ∞ 大于任何实数,而数列的标号只能是实数.
二. 极限
极限: 只能无限接近, 永远触碰不到.
2.11 数列极限的定义
教科书上描述极限定义的语言非常的严谨,且不易懂。这也是本篇博文的重点.
符号语言描述为:
n
→
∞
,
x
n
→
A
n\rightarrow\infty,x_n\rightarrow A
n→∞,xn→A
或者:
lim
n
→
∞
x
n
=
A
\lim_{n\to\infty}{x_n} = A
n→∞limxn=A
箭头代表 趋近于, 即无限接近,但永远不会取到.
A代表:被趋近的那个值.
总含义为:
x (也就是通项公式的因变量) 无限趋近于 ∞ \infty ∞ 时, x n x_n xn 所代表的值 无限趋近于常数 A.
所以千万不要被 lim 式子中的 = 号给蒙了。
其不代表
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
的
值
为
A
x_n 的值为 A
xn的值为A ! ! !
其不代表
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
的
值
为
A
x_n 的值为 A
xn的值为A ! ! !
其不代表
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
的
值
为
A
x_n 的值为 A
xn的值为A ! ! !
而代表:
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
x_n
xn 的值 趋近 为 A ! ! !
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
x_n
xn 的值 趋近 为 A! ! !
n
→
∞
n\rightarrow\infty
n→∞ 时,
x
n
x_n
xn 的值 趋近 为 A ! ! !
2.12 数列极限严谨而又难懂的定义
从古希腊开始,人们就追求数学上的极致严谨。
如何严谨的表示: “当n趋向于无穷大的时候,这个数列的值是无限接近某个值” ??
A: “啥是极限??”
B: “当n趋向于无穷大的时候, 极限就是
X
n
X_n
Xn 无限接近于 A”
A:“我是杠精,你这说的一点也不严谨啊!你说无限接近,这个无限你怎么表示???”
B: “你随便说一个数
ϵ
\epsilon
ϵ(大于0)”
B: “不管你给的
ϵ
\epsilon
ϵ 有多小”
B: “总是存在一个数 n(大于0)”
B: “其
x
n
与
A
的
距
离
值
x_n与A的距离值
xn与A的距离值 比你这个
ϵ
\epsilon
ϵ 要小”
A: “你就吹吧你,你找出这个 N 来给我看看”
B: “你想啊, 0 到 +
∞
\infty
∞ 之间有无限个数. 从
x
0
到
x
∞
x_0 到 x\infty
x0到x∞ 之间也有无限个项”
B: “从
x
0
到
x
∞
x_0到x_\infty
x0到x∞, 与 A 之间的距离越来越小。因为有无限个项, 你就随便给个
ϵ
\epsilon
ϵ>0. 我都能从左往右找,并找到一个
x
n
x_n
xn 与 A 的距离小于你”
A: “你这不是耍流氓嘛。不过确实可以啊”
A: “奥,懂了. 这就是 无限接近 啊”
A"那为啥书上说,存在 N >0, n > N. 使
∣
x
n
−
A
∣
<
ϵ
|x_n - A| < \epsilon
∣xn−A∣<ϵ. 为什么非得用这个 N??"
B:“这个我是真的不会.”
所以,完整的定义为
∀
ϵ
>
0
,
∃
N
>
0
,
当
n
>
N
,
则
∣
x
n
−
A
∣
<
ϵ
\forall\epsilon>0, \exist N>0, 当 n > N, 则 |x_n - A| < \epsilon
∀ϵ>0,∃N>0,当n>N,则∣xn−A∣<ϵ
2.13 数列极限的几何意义
∣
x
n
−
A
∣
<
ϵ
|x_n - A| < \epsilon
∣xn−A∣<ϵ
=
>
ϵ
−
A
<
x
n
<
ϵ
+
A
=> \epsilon-A < x_n < \epsilon+A
=>ϵ−A<xn<ϵ+A
2.14 特别注意
- 数列 x n {x_n} xn的极限与前有限项无关.
- ϵ 与 N 的 作 用 \epsilon 与 N 的作用 ϵ与N的作用
- 几何意义
- 子数列收敛定律:
如果一个数列 xn 有极限,
那么其奇数项构成的数列x2n-1 和 偶数项构成的数列 x2n 都有极限。
而且他们三个的极限都为 A
即同一个数列中
lim
n
→
∞
x
2
n
−
1
=
A
\lim_{n\rightarrow\infty}x_{2n-1} = A
limn→∞x2n−1=A
且
lim
n
→
∞
x
2
n
=
A
\lim_{n\rightarrow\infty}x_{2n} = A
limn→∞x2n=A
如果 A == A, 则数列
x
n
x_n
xn 才有极限,且极限为 A.
2.21 函数的极限
前面我们说过数列的通项公式本质就是函数.
通项公式 x n x_n xn 与 f(x) 是函数的两种不同写法.
但对数列通项函数而言, f(x) 中 x的取值只能为正整数.
这一点很重要,要记住了.
2.22 自变量趋于无穷大时的函数极限
定义
lim
x
→
∞
f
(
x
)
=
A
\lim_{x\to\infty}{f(x)} = A
x→∞limf(x)=A
∀
>
0
,
∃
X
>
0
,
当
x
>
X
,
则
∣
f
(
x
)
−
A
∣
<
ϵ
\forall>0, \exist X>0, 当 x > X, 则 |f(x) - A| < \epsilon
∀>0,∃X>0,当x>X,则∣f(x)−A∣<ϵ
2.23 自变量趋于无穷小时的函数极限
定义
总有一个<-X 的 x比 ξ 小
lim
x
→
∞
f
(
x
)
=
A
\lim_{x\to\infty}{f(x)} = A
x→∞limf(x)=A
∀
ϵ
>
0
,
∃
X
>
0
,
当
x
<
−
X
,
则
∣
f
(
x
)
−
A
∣
<
ϵ
\forall\epsilon>0, \exist X>0, 当 x < -X, 则 |f(x) - A| < \epsilon
∀ϵ>0,∃X>0,当x<−X,则∣f(x)−A∣<ϵ
2.24 自变量趋于无穷时的函数极限
定义
对两边同时约束
lim
x
→
∞
f
(
x
)
=
A
\lim_{x\to\infty}{f(x)} = A
x→∞limf(x)=A
∀
ϵ
>
0
,
∃
X
>
0
,
当
∣
x
∣
>
X
,
则
∣
f
(
x
)
−
A
∣
<
ϵ
\forall\epsilon>0, \exist X>0, 当 |x| > X, 则 |f(x) - A| < \epsilon
∀ϵ>0,∃X>0,当∣x∣>X,则∣f(x)−A∣<ϵ
2.25 自变量趋于定值时的函数极限
当 x → x 0 , f ( x ) ∈ A x\to x_0, f(x)\in A x→x0,f(x)∈A
此时函数 f(x) 的定义域为 x ∈ ( − ∞ , x 0 ) ∣ ∣ x ∈ ( x 0 , + ∞ ) x\in(-\infty, x_0) || x\in(x_0, +\infty) x∈(−∞,x0)∣∣x∈(x0,+∞)
x 只能无限趋近于
x
0
x_0
x0但不能等于 x_0.
如何形容
lim
x
→
x
0
f
(
x
)
=
A
\lim_{x\to x_0}{f(x)} = A
x→x0limf(x)=A 呢??

不管你给的
ϵ
>
0
\epsilon>0
ϵ>0 有多小.
总能找到(一定存在)一个值
ξ
\xi
ξ :
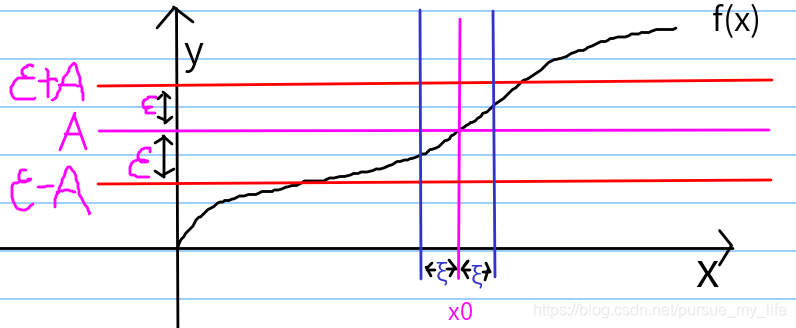
使得
0
<
∣
x
−
x
0
∣
<
ξ
0 < |x-x_0| <\xi
0<∣x−x0∣<ξ 如图所示:

那么这个时候在 两条蓝线中的任意一点,都能找到 一个 x 满足
∣
f
(
x
)
−
A
∣
<
ϵ
|f(x)-A| < \epsilon
∣f(x)−A∣<ϵ
总结
- 默认的,在数列极限中. n → ∞ n\rightarrow\infty n→∞ 就相当于 n → + ∞ n\rightarrow+\infty n→+∞(这是由于定义域,都强调过了)
- 函数极限中则分为
- x → + ∞ x\rightarrow+\infty x→+∞ 单侧
- x → − ∞ x\rightarrow-\infty x→−∞ 单侧
- x → ∞ x\rightarrow\infty x→∞ 两边都考虑
那么就得到一个推论:
lim
x
→
∞
f
(
x
)
=
A
⇔
lim
x
→
+
∞
f
(
x
)
=
lim
x
→
−
∞
f
(
x
)
=
A
\lim_{x\rightarrow\infty}{f(x)=A} \Leftrightarrow \lim_{x\rightarrow+\infty}{f(x)} = \lim_{x\rightarrow-\infty}{f(x)} =A
x→∞limf(x)=A⇔x→+∞limf(x)=x→−∞limf(x)=A
注意: 左极限与右极限都等于 A, 才能推出 极限等于 A.
























 1965
1965

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








