YOLO系列基础（二）Bottleneck瓶颈层原理详解

to 公司数据合规同事，本文为在家编写博客后采用定时发送机制发送的博文，没有用到任何公司信息和公司代码

系列文章地址

YOLO系列基础合集——小白也看得懂的论文精解-CSDN博客

YOLO系列基础（一）卷积神经网络原理详解与基础层级结构说明-CSDN博客

YOLO系列基础（二）Bottleneck瓶颈层原理详解-CSDN博客

YOLO系列基础（三）从ResNet残差网络到C3层-CSDN博客

YOLO系列基础（四）归一化层（BN层）的前世今生！-CSDN博客

YOLO系列基础（五）从神经元共适应性到模型Dropout层-CSDN博客

YOLO系列基础（六）YOLOv1原理详解原理如此清晰-CSDN博客

YOLO系列基础（七）从数据增强到图像线性变换-CSDN博客

YOLO系列基础（八）从坐标直接预测到锚框偏移量-CSDN博客

YOLO系列基础（九）YOLOv2论文及原理详解（上）-CSDN博客

YOLO系列基础（十）YOLOv2论文及原理详解（下）Darknet-19网络结构-CSDN博客

背景

最近在开发与学习过程中，虽然对Bottleneck层大概的原理和作用有所了解，但是每次细细一想，总是对具体的原理不甚清晰。所以花一个下午时间细细整理，做笔记后整理此文

Bottleneck详解

Bottleneck的作用是通过降低通道数来减少计算量，以增加计算与训练效率。

传统的卷积层在每个位置上应用一组较大的滤波器（比如3x3或5x5），以获取局部特征。但是这样的卷积层有时可能会产生过多的计算和参数，尤其是在深层网络中，会导致训练过程缓慢，容易出现梯度消失或爆炸等问题。

瓶颈设计的思想是引入一个瓶颈层，它由一系列不同大小的滤波器组成，通常是1x1、3x3和1x1的卷积层序列

Bottleneck结构图介绍

bottleneck层最初是在ResNet网络中初次提出，通过降低计算量使得神经网络网络深度可以进一步增加。下图为瓶颈层的结构图

左侧是没有瓶颈层的残差网络，对于残差网络我们放置下一篇介绍，此处不用管这个看似很NB的名称。右侧则是称为有瓶颈层的残差网络。有啥区别呢？

左侧仅仅是做了一层常规的3*3卷积核的卷积层，激活之后再次通过另外一次3*3卷积核的卷积层。
右侧则是通过了一层1*1的卷积层、激活之后再通过3*3的卷积层激活之后再一次通过1*1的卷积层。

我为什么要复述一遍……。实际上上面的两个图片完全体现不出bottleneck层的精髓！初看之下觉得莫名其妙，不知所云！因为上诉图片没有写上通道数，而bottleneck层最大的作用就是降低通道数！

针对通道数的问题可以查看

如何理解卷积神经网络中的通道（channel）_神经网络通道数-CSDN博客

这位博主讲的很好，我粘贴部分图片如下，各位可以去上面的博客链接支持一下！

这里输入通道数是3，每个通道都需要跟一个卷积核做卷积运算，然后将结果相加得到一个特征图的输出，这里有4个过滤器，因此得到4个特征图的输出，输出通道数为4。

单个特征图的计算可看下图：

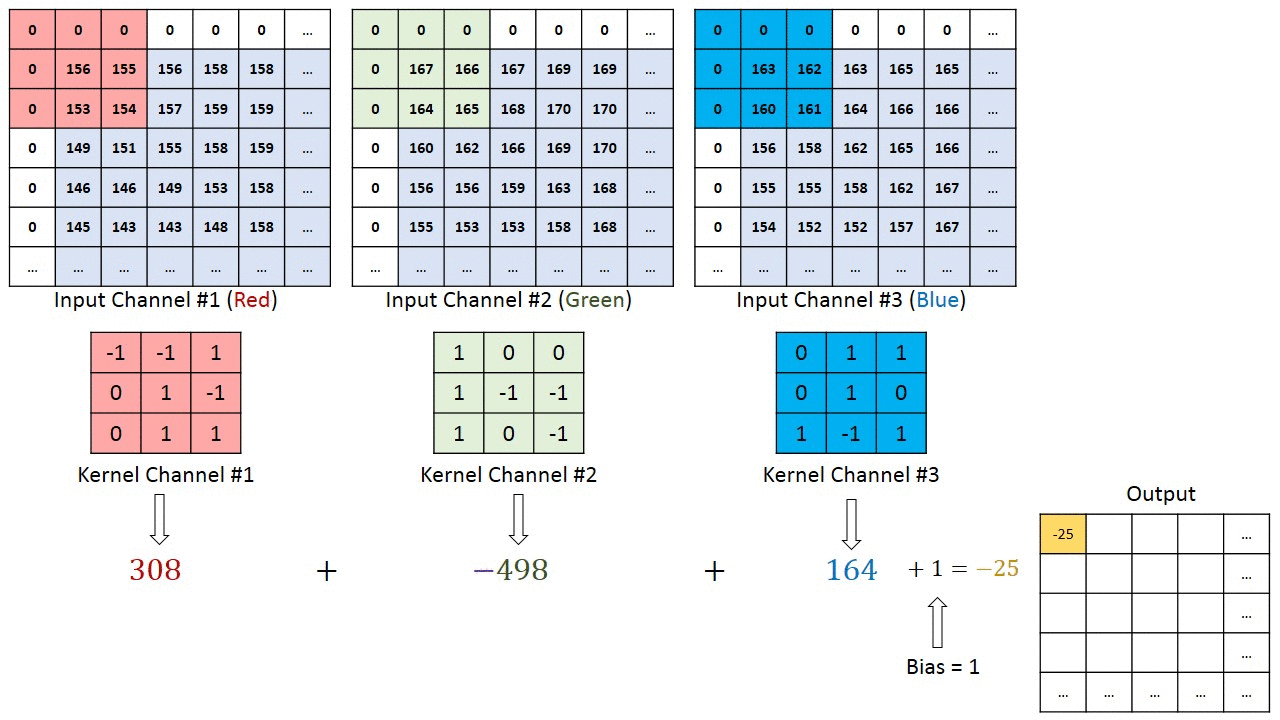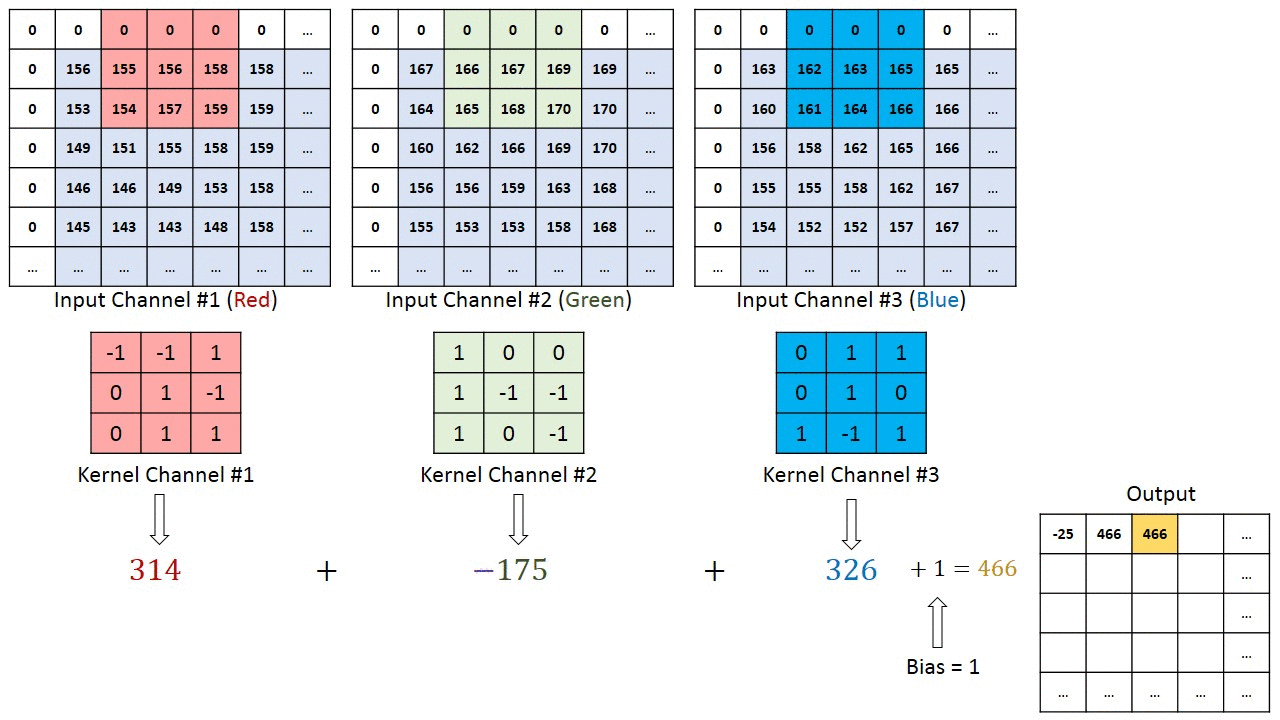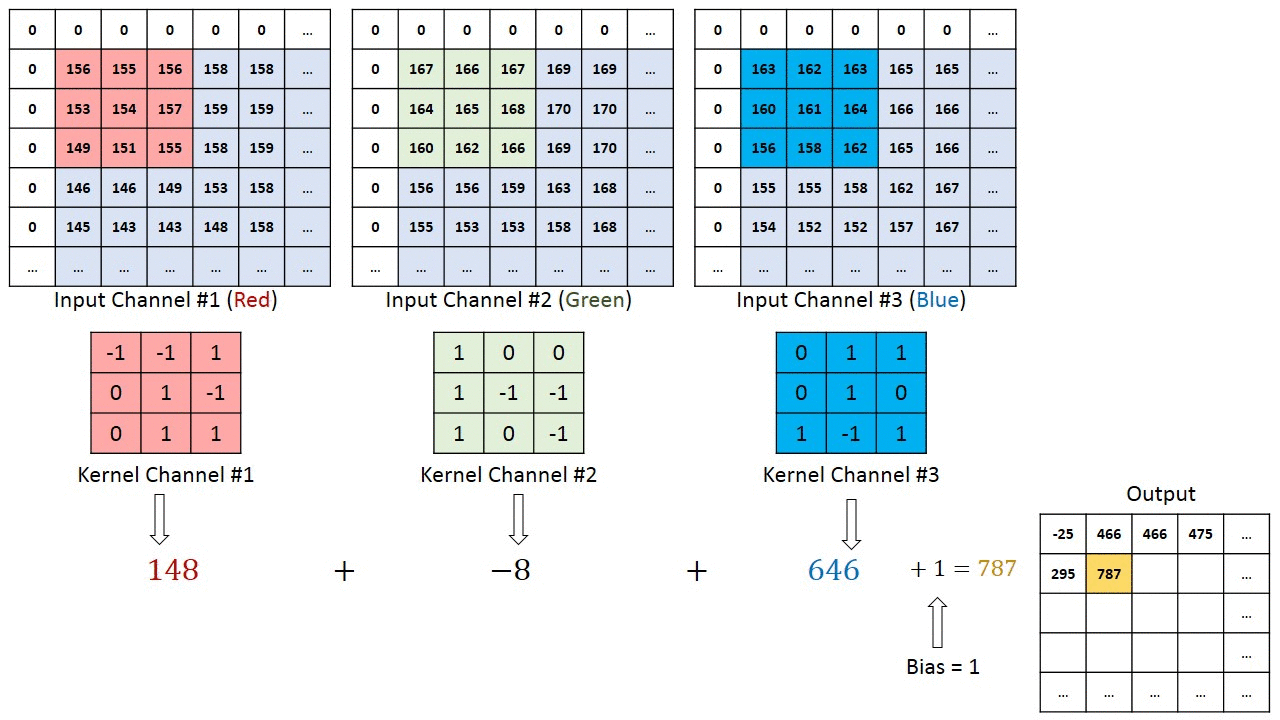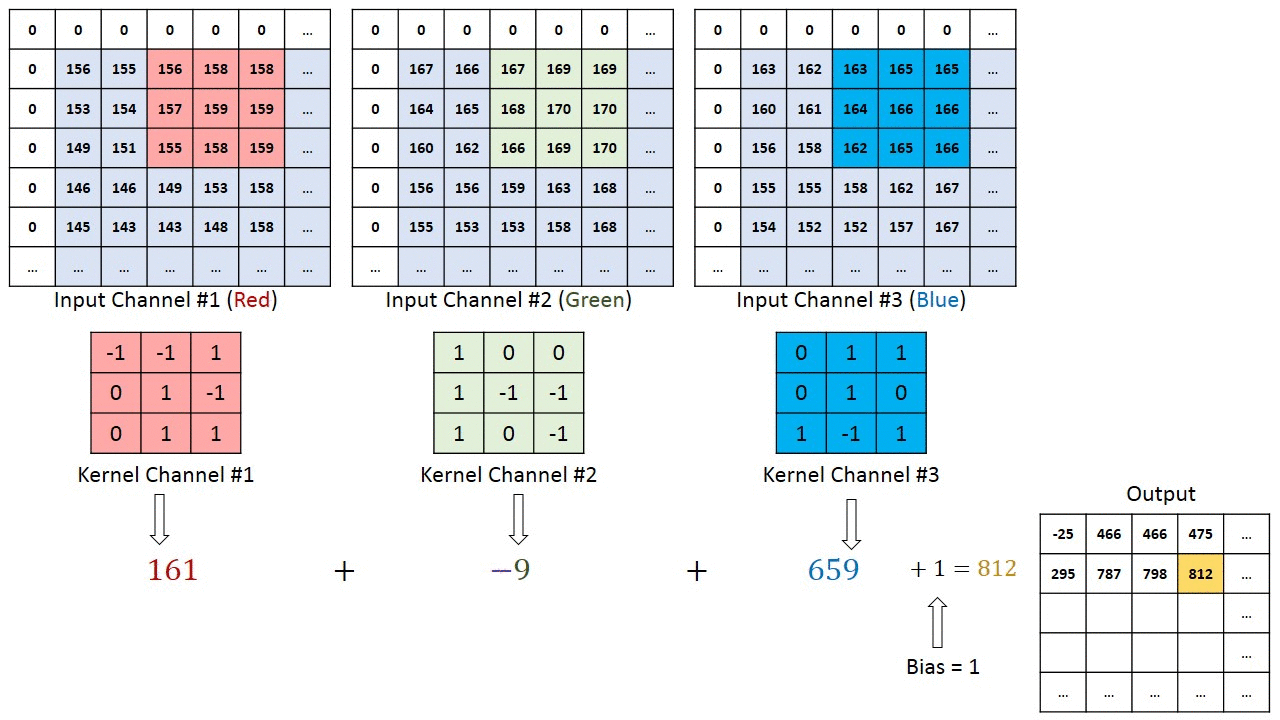
我们对模型结构的图片进行进一步的说明介绍！

左侧结构图介绍

左侧图片从头到尾没有修改通道数，输入图片有多少通道数，计算的时候就有多少通道数被计算。

左侧两层3*3的激活函数的通道数都为256个，即这俩层的卷积层的全写应该是3*3*256

右侧结构图介绍

第一层的卷积层通道数实际上仅有64，全写为1*1*64

第二层的卷积层相应的，也就只有64，全写为3*3*64

第三层的卷积层需要升高通道数回到256，全写为1*1*256

两种方案的参数量比较

我们单看卷积层，不考虑激活函数。

左侧参数量=((3 * 3)(卷积核大小)* 256(单滤波器的卷积核数量)*256(滤波器数量))*2 (一共两层)

= 589824*2

右侧参数量 = (1*1)(卷积核大小)*256(单滤波器的卷积核数量)*64(滤波器数量) + (3*3)(卷积核大小)*64(单滤波器的卷积核数量)*64(滤波器数量) + (1*1)(卷积核大小)*64(单滤波器的卷积核数量)*256((滤波器数量)) = 69632

显然右侧参数量远远小于左侧

Bottleneck层模型介绍

瓶颈设计的思想是引入一个瓶颈层，它由一系列不同大小的滤波器组成，通常是1x1、3x3和1x1的卷积层序列：

第一个1x1卷积层：用于减少通道数，即降维，从而降低计算复杂度。
3x3卷积层：用于提取空间特征，是瓶颈块中的核心部分，用于提取图像中的细节信息。
第二个1x1卷积层：用于恢复通道数，即升维，以便与输入进行相加。

这样的设计可以有效地减少特征图的维度，从而减少计算量和参数数量。此外，1x1的卷积层还可以用来引入非线性变换。瓶颈设计的名称“bottleneck”（瓶颈）来自于它的结构，因为在特征图经过1x1的卷积核降维后，其通道数被显著地减小，形象地类似于瓶颈的形状。

Bottleneck层的代码示例

import torch
import torch.nn as nn
import torch.nn.functional as F

class Bottleneck(nn.Module):
    expansion = 4  # 输出的通道数通常是输入的4倍

    def __init__(self, in_channels, out_channels, stride=1, downsample=None):
        super(Bottleneck, self).__init__()
        # 第一个1x1卷积，减少通道数
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=1, bias=False)
        # BN层和ReLU激活函数
        self.bn1 = nn.BatchNorm2d(out_channels)
        # 第二个3x3卷积，用于特征提取
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=stride,
                               padding=1, bias=False)
        self.bn2 = nn.BatchNorm2d(out_channels)
        # 第三个1x1卷积，恢复通道数
        self.conv3 = nn.Conv2d(out_channels, out_channels * self.expansion, kernel_size=1, bias=False)
        self.bn3 = nn.BatchNorm2d(out_channels * self.expansion)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

# 示例：创建一个Bottleneck层
in_channels = 64
out_channels = 64
bottleneck = Bottleneck(in_channels, out_channels, stride=1)

# 测试Bottleneck层
x = torch.randn(1, in_channels, 56, 56)  # 假设输入是(batch_size, in_channels, height, width)
out = bottleneck(x)
print(out.shape)  # 输出形状应该是 (1, 64*4, 56, 56) 因为 expansion=4