一些数学公式证明

神气爱哥

已于 2023-09-24 22:09:48 修改

阅读量81

点赞数

文章标签：算法

于 2023-08-14 11:41:43 首次发布

本文链接：https://blog.csdn.net/qingcaichongchong/article/details/132272895

版权

1. 最小二乘问题的几种证法

1.1

考虑最小二乘问题: $min(\left \| AX-b \right \|)$ ，AX表示在A线性空间中的一组线性组合而成的一个向量，使其到b向量距离最短，由于最小二乘是超定方程，所以b向量维度比AX维度高的，什么时候取到最短，当且仅当 $(b-AX)\perp A$ 时，如图所示：

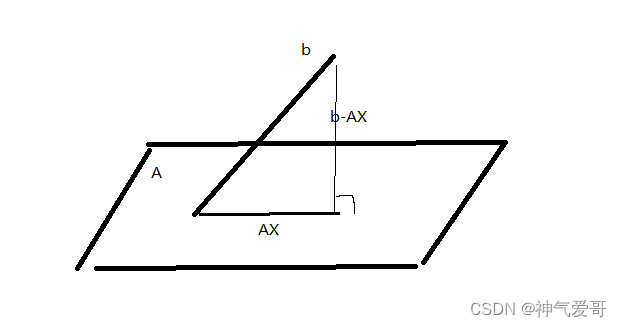
b-AX垂直于A的向量空间，则有： $A^T(b-AX)=A^Tb-A^TAX=0$

得证: $X=(A^TA)^{-1}A^Tb$

1.2

$\left \| AX-b \right \|^2=(AX-b)^T(AX-b)=X^TA^TAX-X^TA^Tb-b^TAX+b^Tb$

取到极值时，倒数为0

再根据矩阵求导法则 $(X^TA)^{'}=(A^TX)^{'}=A$ :

$2A^TAX-2A^Tb=0$ ，得证

2. 为什么海森矩阵半正定不能确定最小值

因为 $f(x+\delta x)\approx f(x) + f^{'}(x)x+\frac{1}{2}f^{''}(x)x$ ，由于在极值处 $f^{'}(x)$ 值为0，因此， $f(x)$ 是否时极值取决于 $f^{''}(x)$ 的符号，当 $f^{''}(x)$ 也为0时，就要取决于更高次的导数了，因此半正定无法确定最小值。反之，如果 $f^{''}(x)$ 为正定矩阵，则 $f(x)$ 肯定在x处取得最小值

3. 样本方差为什么是 $s^2=\frac{n-1}{n}\sigma^2$

证明：

$E(s^2)=E(\frac{1}{n}\sum (x_i-\bar{x})^2)=E(\frac{1}{n}\sum [(x_i-u)-(\bar{x}-u)]^2)$

$=E(\frac{1}{n}\sum [(x_i-u)^2-2(x_i-u)(\bar{x}-u)+(\bar{x}-u)^2])=E(\frac{1}{n}[n\sigma^2-n(\bar{x}-u)^2])$

又因为

$\bar{x}=\frac{1}{n}(x_0-u)+\frac{1}{n}(x_1-u)+...+\frac{1}{n}(x_i-u)$

所以，根据泰勒公式及协方差传播定律有：

$E(\bar{x}-u)^2=D(\bar{x})=\frac{1}{n^2}\sigma^2+\frac{1}{n^2}\sigma^2+...+\frac{1}{n^2}\sigma^2=\frac{1}{n}\sigma^2$

带入上式得：

$E(s^2)=\frac{n-1}{n}\sigma^2$

4. 李代数伴随矩阵证明

To expand on the existing answer: for me the tricky part was actually going from eq. 23 to eq. 24. There's probably an easier way to see it, but here's how I did it.

Recall that for a vector uu, the matrix u×u× is defined as the linear transformation

u×::v↦u×v.u×::v↦u×v.

So the identity R⋅ω×⋅R−1=(Rω)×R⋅ω×⋅R−1=(Rω)× can be intuitively interpreted as "[unrotating, then crossing with ωω, then rotating] is the same as [crossing with a rotated ωω]". We can prove this identity by letting the RHS of the identity act upon an arbitrary vector vv:

(Rω)×v=(Rω)×v=(Rω)×(RR−1v)=R[ω×(R−1v)]=Rω×R−1v,(Rω)×v=(Rω)×v=(Rω)×(RR−1v)=R[ω×(R−1v)]=Rω×R−1v,

where we have used the fact that for any rotation matrix UU and vectors a,ba,b we have

(Ua)×(Ub)=U(a×b)

神气爱哥

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
打赏
0
评论
一些数学公式证明

To expand on the existing answer: for me the tricky part was actually going from eq. 23 to eq. 24. There's probably an easier way to see it, but here's how I did it.Recall that for a vector uu, the matrix u×u× is defined as the linear transformationu×::v↦u
复制链接

扫一扫