为什么可以用概率分布密度函数来表示概率？

为什么经常会看到随机变量的概率分布多用概率密度函数来描述而不直接用概率分布函数？

举个例子：现有如下数据集X，m个样本n个特征，y为标签向量集合，假设各维度遵循高斯分布

概率分布密度函数(高斯分布)如下所示，

 这里的cov表示协方差矩阵，为均值向量。 我们经常会看到一些文章中的公式，如下所示

 式中p(x)为全概率公式，如下所示：

可以看到，公式中“直接用概率分布密度函数来表示概率”，如下

        这样表示对吗？要知道概率分布密度函数的值是可能大于1的。之所以这样做，一方面是因为概率的分布函数不好写出来，另一方面是因为过程省略了一些步骤，如下所示

  是每个类的一个常量乘法因子，在之后的对后验概率进行规范化的时候就抵消掉了。因此可以直接使用来估计类条件概率，如下所示

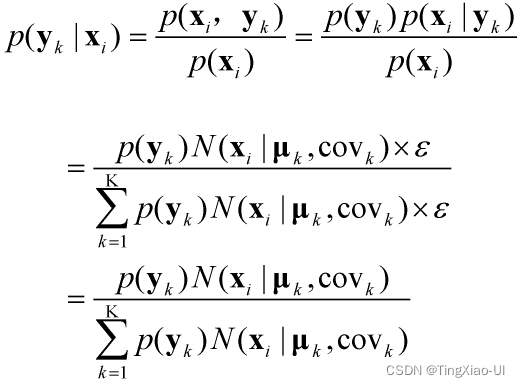
         首先，概率分布函数和概率分布密度函数是两个概念，并不能用概率分布密度函数直接来表示概率，即"质量"不能直接用“密度”来表达。你之所以会有“为什么可以用概率分布密度函数来表示概率”这种感觉，可能只是因为有些人少写了某些步骤而已。