图论专题总结—最短路

        时间非常有限，但还是强忍着对这个专题进行总结。一方面阶段性总结是“磨刀不误砍柴工”的最有效方法之一；二是在学习这个专题的时候看到很多大牛们的总结帖都是受益匪浅的，让其他人少走了很多弯路，自己也可以随时进行温故而知新。废话少说，看第一个小专题最短路问题。

       常见的最短路算法有Dijkstra、Floyd、Bellman-Ford、SPFA等这几种，由于网上的知识讲解和算法分析都非常详细了，这里只做简单的描述，重点放在了算法的模板上哈。先来看一下这几个算法的大概比较：

最短路算法	核心思想	可实现方法	时间复杂度	约束条件以及使用范围
Dijkstra	贪心	邻接矩阵、邻接表、优先队列、Vector、堆	O(n^2)	适用于权值为非负的图的单源最短路径
Bellman-Ford	迭代	邻接表、FIFO队列、Vector	O(nm)	适用于权值有负值的图的单源最短路径，并且能够检测并输出负圈
Floyd	DP	邻接矩阵	O(n^3)	适用于多个结点间的最短路径
SPFA	优化Bellman-Ford（队列优化，减少冗余松弛）	邻接表、FIFO队列、Vector	O(kE)	与Bellman-Ford类似，但不能输出负圈，稀疏图速度更快

     Ø  Dijkstra算法

         一般我们熟知的Dijkstra算法是求解两点之间的最短路，而了解算法的都知道它是单源最短路（SSSP），即可以计算从起点出发到每个点的最短路。这一特性也经常用来与其他算法结合使用，用来做其他算法的预处理，例如在图搜索里，要求每个点到终点的最短路径时，该算法就可以做到足够的优化处理了。

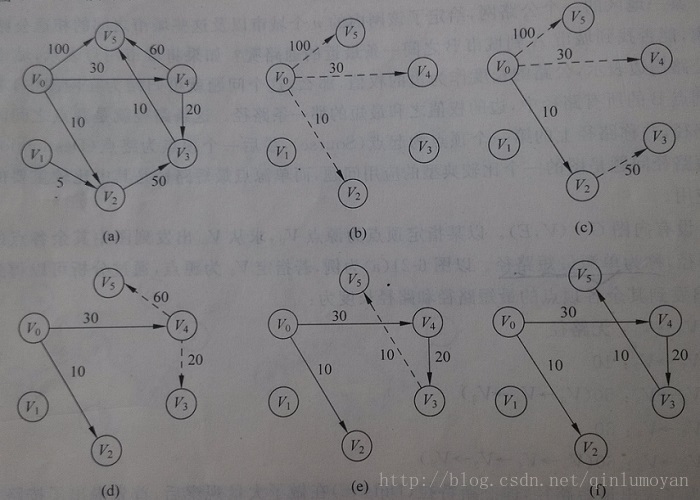
       如果你是初次接触，那我们先来简单看看这个算法吧。个人觉得文字的描述始终没问图文的形象，看下面这张Dijkstra算法过程图：

       该图简单地描述了算法的过程，虽然不是很全，但能够看到算法的过程了，还是不了解可以搜点资料哈。

       Dijkstra算法其实质是贪心，时间复杂度为O(N^2)，对应的伪代码如下：

Dijkstra(){ 
    清除所有点的标号
    设dist[0]等于0，其他的dist[i]为INF
    进行n次循环{
        在所有未标号结点中，选出d值最小的结点x
        标记结点x
        对于从x出发的所有边（x,y），更新dist[y]=min{dist[y],dist[x]+w[x,y]}
    }
}

       源代码实现的直观code：

const int MAXN = N; //结点数
const int INF = 0x3fffffff; //最小值
int vis[MAXN],dist[MAXN],map[MAXN][MAXN];  //vis为访问标记，dist为到每个点的最短路径值，map为图的关系
int n; //接收结点数
void Dijkstra(){
    memset(vis,0,sizeof(vis)); //清除所有标号
    for(int i=1;i<=n;i++) dist[i]=(i==1 ? 0 : INF); //设d[1]=0，其它置为INF
    for(int i=1;i<=n;i++){ //进行n次循环
        int x,min=INF;
        for(int j=1;j<=n;j++) if(!vis[j] && dist[j]<=min) min=dist[x=j]; //在所有未标记的节点中，选出d值最小的节点x
        vis[x]=1;  //标记x节点
        for(int k=1;k<=n;k++) //对于从x出发的所有边（x，k）进行最小值更新
            if(dist[k]>dist[x]+map[x][k])
                dist[k] = dist[x]+map[x][k];
    }
}

       上述采用的是邻接矩阵进行存储的，然而如果数据量大、时间卡的很紧的题目，这样是不可行的，下面是一种邻接表+优先队列的优化code：

typedef pair<int,int> pii;  //把两个类型捆绑在一起
const int MAXN=N; //N为最大结点值
const int MAXM = MAXN*MAXN;
const int INF=0x3fffffff;
int n,m,a,b;
int first[MAXN],next[MAXM];  //first[u]保存结点u的第一条边编号，next[e]保存编号为e的下一条边的编号
int u[MAXM],v[MAXM],w[MAXM],d[MAXN];
bool done[MAXN];  //记录是否被取出过

void read_gragh(){
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++) first[i]=-1;  //初始化表头
    for(int i=0;i<2*m;i++){
        scanf("%d%d%d",&a,&b,&w[i]);
        u[i]=--a;v[i]=--b;
        next[i]=first[u[i]];  //插入链表
        first[u[i]]=i;
        next[++i]=first[v[i]];  //如果是无向边，需要反向插入一次
        first[v[i]]=i;
        u[i]=v[i-1];v[i]=u[i-1];w[i]=w[i-1];  //将边进行关联
    }
}

void Dijkstra(){
    priority_queue<pii,vector<pii>,greater<pii> > q;  //定义一个二元组的优先队列
    for(int i=0;i<n;i++) d[i]=(i==0?0:INF);  //初始化
    memset(done,0,sizeof(done));
    q.push(make_pair(d[0],0)); //起点进入队列
    while(!q.empty()){
        pii u=q.top();q.pop();
        int x=u.second;
        if(done[x]) continue;  //已经计算过则跳过
        done[x]=true;
        for(int e=first[x];e!=-1;e=next[e])
            if(d[v[e]]>d[x]+w[e]){
                d[v[e]]=d[x]+w[e];   //松弛，更新值
                q.push(make_pair(d[v[e]],v[e]));
            }
    }
}

       最后，给一个比较常用的模板，用结构体来保存加权图的code（核心部分已给出解释，不再赘述，对不同部分进行注释）：

const int MAXN = N;
const int INF = 0x3fffffff;
int t,n,m,a,b,w;

struct edge{
    int from,to,dist; //dist为距离
};

struct heapnode{ //优先队列结点
    int d,u;
    bool operator < (const heapnode& rhs) const{
        return d>rhs.d;
    }
};

struct Dijkstra{
    int n,m;
    vector<edge> edges; //边列表
    vector<int> g[MAXN]; //每个结点出发的边编号
    bool done[MAXN]; //是否标记
    int d[MAXN]; //s到各个点的距离
    int p[MAXN];  //最短中的上一条边

    void init(int n){
        this->n=n;
        for(int i=0;i<n;i++) g[i].clear();  //清空邻接表
        edges.clear();  //清空边表
    }

    void addedge(int from,int to,int dist){  //增加边
        edges.push_back((edge){from,to,dist});
        m=edges.size();
        g[from].push_back(m-1);
    }

    void dijkstra(int s){
        priority_queue<heapnode> q;
        for(int i=0;i<=n;i++) d[i]=INF;
        d[s]=0;
        memset(done,0,sizeof(done));
        q.push((heapnode){0,s});
        while(!q.empty()){
            heapnode x= q.top();q.pop();
            int u= x.u;
            if(done[u]) continue;
            done[u]=true;
            for(int i=0;i<g[u].size();i++){
                edge& e = edges[g[u][i]];
                if(d[e.to]>d[u]+e.dist){
                    d[e.to]=d[u]+e.dist;
                    p[e.to]=g[u][i];
                    q.push((heapnode){d[e.to],e.to});
                }
            }
        }
    }
}

     Ø  Bellman-Ford算法、SPFA算法

        如果图的边权值存在负权值时，上述的Dijkstra算法就不可行了，那么针对这个问题，Bellman-Ford算法可以很好地解决，它通过不停迭代对不含环的路径进行n-1个结点进行松弛操作来获取最短路径。对应的核心代码如下：

const int MAXN = N;  
const int INF = 0x3fffffff;  
int dist[MAXN],u[MAXN],v[MAXN],w[MAXN],d[MAXN];  
int n,m;  
  
void Bellman_Ford(){  
    for(int i=1;i<=n;i++) dist[i]=(i==1?0:INF); //初始化  
    for(int k=1;k<=n;k++) //迭代  
        for(int i=1;i<=2*m;i++){  
            int x=u[i],y=v[i];  
            if(dist[x]<INF)  
                if(dist[y]>dist[x]+w[i])  
                    dist[y] = dist[x]+w[i];  
        }  
} 

       然而，Bellman-Ford算法的时间复杂度还是不容乐观的，因此我们用队列来进行循环检查，可以使得其最坏情况下为O(nm)的复杂度，其code模板为：

struct edge{
    int from,to,dist;
};
vector<edge> edges;
vector<int> g[MAXN*2];
bool inq[MAXN]; //是否在队列中
int d[MAXN];  //s到各个点的距离
int p[MAXN]; //最短路中的上一条弧
int cnt[MAXN]; //进队次数，入队n次则可以判断存在负圈

void init(int n){
    for(int i=0;i<n;i++) g[i].clear();
    edges.clear();
}

void addedge(int from,int to,int dist){
    edges.push_back((edge){from,to,dist}); //建图
    int mm=edges.size();  //获取大小
    g[from].push_back(mm-1);
}

bool bellman_ford(){
    queue<int> q;
    memset(inq,0,sizeof(inq));
    memset(cnt,0,sizeof(cnt));
    for(int i=0;i<n;i++){ //初始化
        d[i]=INF;inq[0]=true;
        q.push(i);
    }
    while(!q.empty()){
        int u=q.front();q.pop();
        inq[u]=false;  //清除在队列中的标记
        for(int i=0;i<g[u].size();i++){
            edge& e=edges[g[u][i]];
            if(d[e.to]>d[u]+e.dist){
                d[e.to]=d[u]+e.dist;
                p[e.to]=g[u][i];
                if(!inq[e.to]){ //如果已经存在就不重复添加
                    q.push(e.to);
                    inq[e.to]=true;
                    if(++cnt[e.to]>n) //判断负圈，入队n次说明存在
                        return true;
                }
            }
        }
    }
    return false;
}

      针对这个问题对其松弛操作进行优化处理，SPFA算法的方法为：用数组d记录每个结点的最短路径估计值，而且用邻接表来存储图G。采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止。

void SPFA(){  
    memset(vis,0,sizeof(vis));  
    for(int i=1;i<=n;i++) dist[i]=(i==s ? 0 :INF); //初始化  
    queue<int> q;  
    q.push(s);//起点放入队列  
    vis[s]=1;//标记  
    while(!q.empty()){  
        int tmp=q.front(); //取队首元素  
        q.pop();  
        vis[tmp]=0; //记得标记  
        for(int i=1;i<=n;i++){  
            if(dist[i]>dist[tmp]+map[tmp][i]){  
                dist[i]=dist[tmp]+map[tmp][i];  
                if(!vis[i]){  
                    q.push(i);  
                    vis[i]=1;  
                }  
            }  
        }  
    }  
} 

     Ø  Floyd算法

        当需要求出图中多组点之间的最短路径时，上述几种方法就需要调用多次。对于此问题这里有一个简单的算法，即Floyd算法。该算法类似于DP，其状态转移方程为： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}。

        该算法的过程为：把图用邻接矩阵G表示出来，如果从Vi到Vj有路可达，则G[i,j]=d，d表示该路的长度；否则G[i,j]=无穷大。定义一个矩阵D用来记录所插入点的信息，D[i,j]表示从Vi到Vj需要经过的点，初始化D[i,j]=j。把各个顶点插入图中，比较插点后的距离与原来的距离，G[i,j] = min( G[i,j], G[i,k]+G[k,j] )，如果G[i,j]的值变小，则D[i,j]=k。在G中包含有两点之间最短道路的信息，而在D中则包含了最短通路径的信息。

        对应的核心代码如下（虽然code只有短短的五行，但是其作用远不止这些，可以好好体会下，非常重要的）：

void Floyd(){  
    for(int k=1;k<=n;k++)  
        for(int i=1;i<=n;i++)  
            if(map[i][k]!=INF) //优化减少循环  
                for(int j=0;j<=n;j++)//DP  
                    if(map[i][j]>map[i][k]+map[k][j])  
                        map[i][j]=map[i][k]+map[k][j];  
} 

      Ø 入门训练

       虽然上述算法的核心部分都不长和复杂，但在竞赛中其作用是非常大的，变形也是非常多的，只有真正掌握了核心部分，能够不假思索地拍出来，才是对其真正的掌握，最后给出几道比较基础的题目可以用来练练手（更新中......）：

       HDU 2544、1874、2112、2066

       PKU 2387、3259

      这几道题都可以作为最短路的入门题，都只需要很简单的变换即可，也可以用多种最短路算法进行code。详见【解题报告】。