菜鸟福利 A星寻路算法 cocos2d-x实现

    这篇blog是翻译自iOS Tutorial Team的成员 Johann Fradj，他目前是一位全职的资深iOS开发工程师。他是HotApps Factory的创始人，该公司开发了AppCooker

你是否在做一款游戏的时候想实现一种寻路算法，让一些怪兽或者游戏主角，让它们移动到特定的位置，避开墙壁和障碍物呢？
     如果是的话，请看这篇教程，我们会展示如何使用著名的A星寻路算法来实现它！

     公式表示为： f(n)=g(n)+h(n),

      其中 f(n)是从初始点经由节点n到目标点的估价函数，

      g(n) 是在状态空间中从初始节点到n节点的实际代价，

      h(n) 是从 n 到目标节点最佳路径的估计代价

      在网上已经有很多篇关于A星寻路算法的文章，但是大部分都是提供给已经了解基本原理的高级开发者的,相信你绞尽脑汁看了之后只记得个公式 f=g+h其他的全是浮云，这个公式相信你也一定怎么看都是天书一样。而你又不敢向那些高手大牛们抱怨什么，因为在他们看来，你只是个菜鸟，你看不懂只是你智商问题，跟他们没有任何关系。 如果你学历尚可那大学课程也一定有教授讲授过，但你扪心自问，教授讲的你听懂了吗？而老师关心过学生听没听懂这个问题了吗？

      再精妙的计算机原理，如果看不懂的话， 那就什么用也没有。这不知道是多么尴尬的事情。但谁也没规定这个寻路算法只是大牛或专家们的专利。

     F=G+H倒底是什么意思？不用着急，本篇教程面向菜鸟，将从最基本的原理讲起。我们会一步步讲解A星寻路算法，幷配有很多图解和例子，力争让你搞懂，并能应用在实际上，而决不只停留在书本成为好看的花瓶。

     一只找不到回家路的小猫
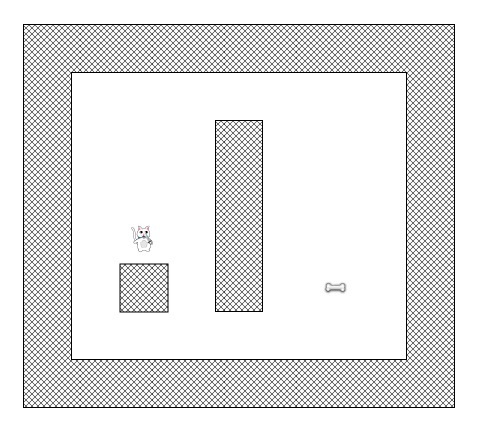
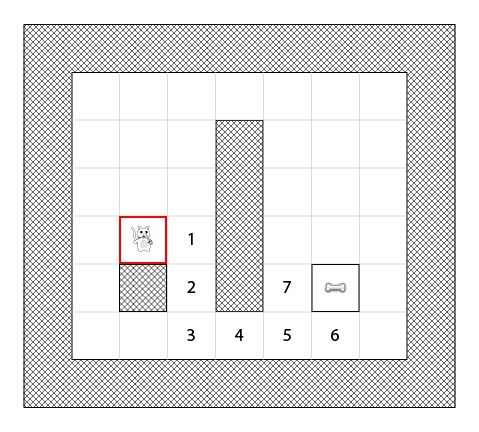
      让我们想象一下，有一款游戏，游戏中一只猫想要找到获取骨头的路线。

“为什么会有一只猫想要骨头？！”你可能会这么想。在本游戏中， 这是一只聪明的猫，他想捡起骨头并不是自己想吃，而是贿赂给挡在路上的狗，以防止被恶狗咬死！

     现在想像一下下图中的猫想找到到达骨头的最短路径：

      看的出，猫不能直接从它当前的位置走到骨头的位置，因为有面墙挡住了去路，而且它在游戏中不是一只幽灵猫！
      游戏中的猫同样懒惰，它总是想找到最短路径，这样当他回家时不会太累:-)

但是我们如何编写一个算法计算出猫要选择的那条路径呢？A星算法拯救了我们！

简化搜索区域

寻路的第一步是简化成容易控制的搜索区域
 怎么处理要根据游戏来决定了。例如，我们可以将搜索区域划分成像素点，但是这样的划分粒度对于我们这款基于方块的游戏来说太高了（没必要）。

作为代替，我们使用方块（一个正方形）作为寻路算法的单元。其他的形状类型也是可能的（比如三角形或者六边形），但是正方形是最简单并且最适合我们需求的。 

像那样去划分，我们的搜索区域可以简单的用一个地图大小的二维数组去表示。所以如果是25*25方块大小的地图，我们的搜索区域将会是一个有625个正方形的数组。如果我们把地图划分成像素点，搜索区域就是一个有640，000个正方形的数组了（一个方块是32*32像素）！

现在让我们基于目前的区域，把区域划分成多个方块来代表搜索空间（在这个简单的例子中，7*6个方块 = 42 个方块）：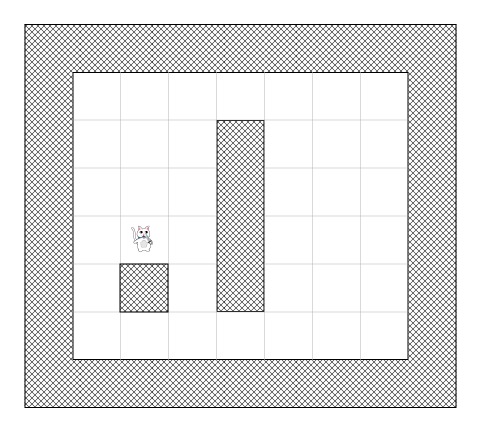

Open表和Close表

除了懒惰之外，我们的猫没有好的记忆力，所以它需要两个列表：

1.一个记录下所有被考虑来寻找最短路径的方块（称为open 列表）

2.一个记录下不会再被考虑的方块（成为closed列表）

猫首先在closed列表中添加当前位置（我们把这个开始点称为点 “A”）。然后，把所有与它当前位置相邻的可通行小方块添加到open列表中。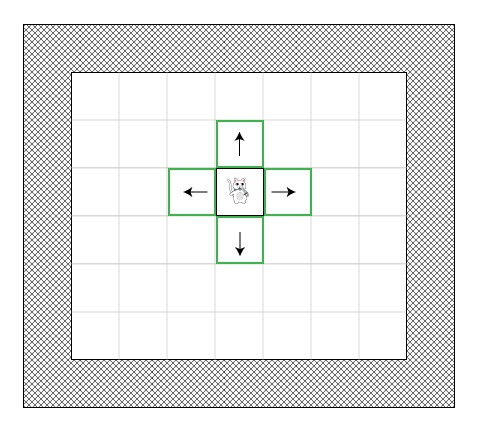

上图是猫在某一位置时的情景（绿色代表open列表）:

 现在猫需要判断在这些选项中，哪项才是最短路径，但是它要如何去选择呢？

 在A星寻路算法中，通过给每一个方块一个和值，该值被称为路径增量。让我们看下它的工作原理！

路径增量

我们将会给每个方块一个G+H和值：

•G是从开始点A到当前方块的移动量。所以从开始点A到相邻小方块的移动量为1，该值会随着离开始点越来越远而增大。

•H是从当前方块到目标点（我们把它称为点B，代表骨头！）的移动量估算值。这个常被称为探视，因为我们不确定移动量是多少 – 仅仅是一个估算值。

 你也许会对“移动量”感兴趣。在游戏中，这个概念很简单 – 仅仅是方块的数量。

 

然而，在游戏中你可以对这个值做调整。例如：

•如果你允许对角线移动，你可以针对对角线移动把移动量调得大一点。

•如果你有不同的地形，你可以将相应的移动量调整得大一点 – 例如针对一块沼泽，水，或者猫女海报:-)

 这就是大概的意思 – 现在让我们详细分析下如何计算出G和H值。

关于G值：

G是从开始点A到达当前方块的移动量（在本游戏中是指方块的数目）。

 为了计算出G的值，我们需要从它的前继（上一个方块）获取，然后加1。所以，每个方块的G值代表了从点A到该方块所形成路径的总移动量。

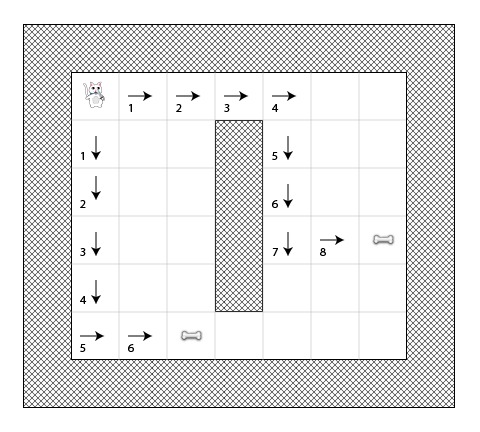
 例如，下图展示了两条到达不同骨头的路径，每个方块都标有它的G值：

关于H值

H值是从当前方块到终点的移动量估算值（在本游戏中是指方块的数目）。

 移动量估算值离真实值越接近，最终的路径会更加精确。如果估算值停止作用，很可能生成出来的路径不会是最短的（但是它可能是接近的）。这个题目相对复杂，所以我们不会再本教程中讲解，但是我在教程的末尾提供了一个网络链接，对它做了很好的解释。

 为了让它更简单，我们将使用“曼哈顿距离方法”（也叫“曼哈顿长”或者“城市街区距离”），它只是计算出距离点B，剩下的水平和垂直的方块数量，略去了障碍物或者不同陆地类型的数量。

 例如，下图展示了使用“城市街区距离”，从不同的开始点到终点，去估算H的值（黑色字）：

A星算法

既然你知道如何计算每个方块的和值（我们将它称为F，等于G+H),  我们来看下A星算法的原理

猫会重复以下步骤来找到最短路径：

1.将方块添加到open列表中，该列表有最小的和值。且将这个方块称为S吧。

2.将S从open列表移除，然后添加S到closed列表中。

3.对于与S相邻的每一块可通行的方块T：

1.如果T在closed列表中：不管它。

2.如果T不在open列表中：添加它然后计算出它的和值。

3.如果T已经在open列表中：当我们使用当前生成的路径到达那里时，检查F 和值是否更小。如果是，更新它的和值和它的前继。

 

如果你对它的工作原理还有点疑惑，不用担心 – 我们会用例子一步步介绍它的原理！:]

猫的路径

让我们看下我们的懒猫到达骨头的行程例子。

 

在下图中，我根据以下内容，列出了公式F = G + H 中的每项值：

•F（方块的和值）：左上角

•G（从A点到方块的移动量）：左下角

•H（从方块到B点的估算移动量): 右下角

 

同时，箭头指示了到达相应方块的移动方向。

 

最后，在每一步中，红色方块表示closed列表，绿色方块表示open列表。

好的，我们开始吧！

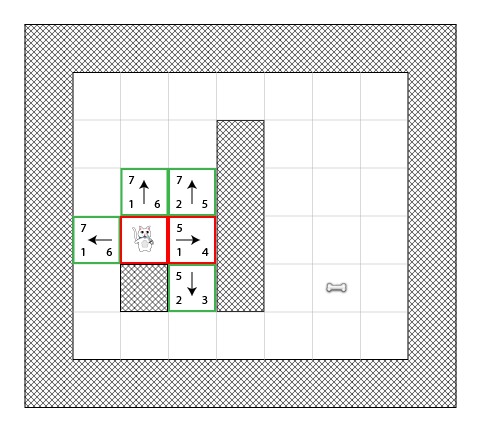
第一步，猫会确定相对于开始位置（点A）的相邻方块，计算出他们的F和值，然后把他们添加到open列表中：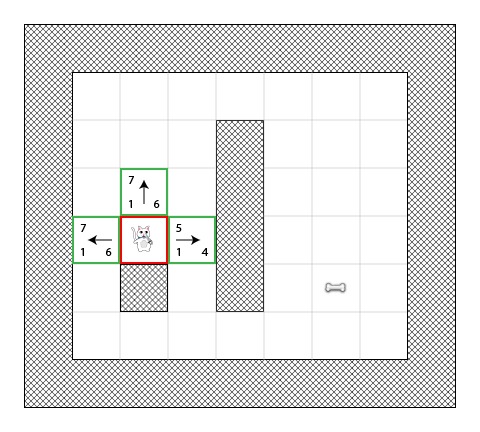

你会看到每个方块都列出了H值（有两个是6，一个是4）。我建议根据“城市街区距离”去计算方块的相关值，确保你理解了它的原理。

 同时注意F值（在左上角）是G（左下角）值和H（右下脚）值的和

 第二步

 在第二步中，猫选择了F和值最小的方块，把它添加到closed列表中，然后检索它的相邻方块的相关数值。

现在你将看到拥有最小增量的是F值为4的方块。猫尝试添加所有相邻的方块到open列表中（然后计算他们的和值），除了猫自身的方块不能添加以外（因为它已经被添加到了closed列表中）或者它是墙壁方块（因为它不能通行）。

注意被添加到open列表的两个新方块，他们的G值都增加了1，因为他们现在离开始点有2个方块远了。你也许需要再计算下“城市街区距离”以确保你理解了每个新方块的H值。

第三步
再次，我们选择了有最小F和值（5）的方块，继续重复之前的步骤：

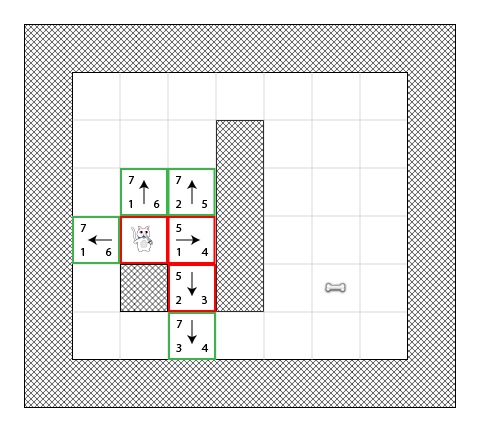
现在，只有一个可能的方块被添加到open列表中了，因为已经有一个相邻的方块在close列表中，其他两个是墙壁方块。

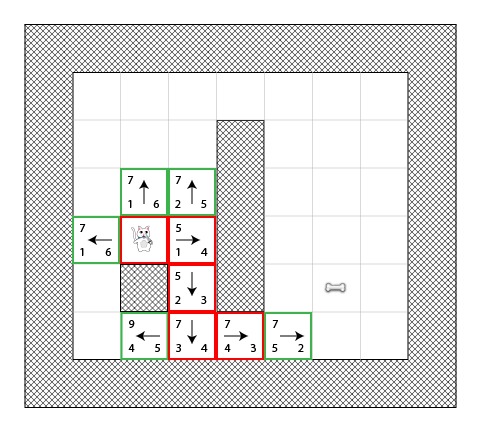
第四步

现在我们遇到了一个有趣的情况。正如你之前看到的，有4个方块的F和值都为7 –我们要怎么做呢？！

 有几种解决方法可以使用，但是最简单（快速）的方法是一直跟着最近被添加到open列表中的方块。现在继续沿着最近被添加的方块前进。

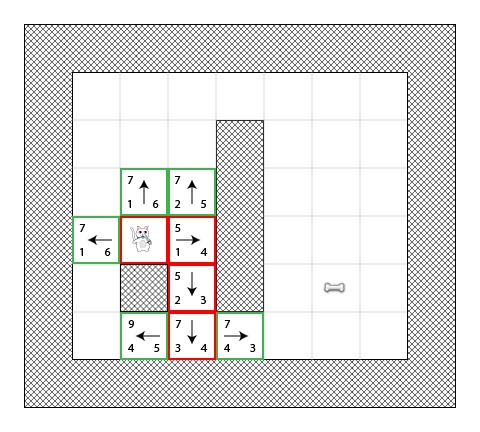
这次有两个可通过的相邻方块了，我们还是像之前那样计算他们的和值。

第五步

 接着我们选择了最小和值（7）的方块，继续重复之前的步骤：

现在，我们已经越来越接近终点了！

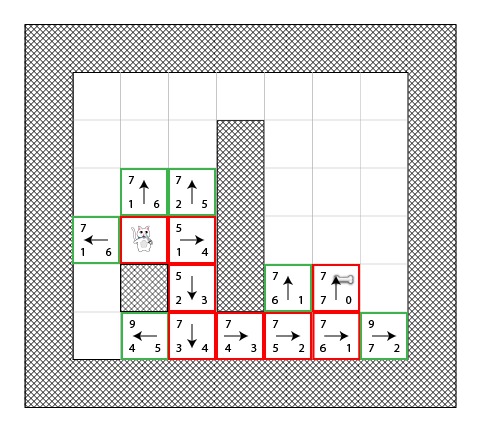
第六步

 你现在训练有素了！我打赌你能够猜出下一步是下面这样子了：

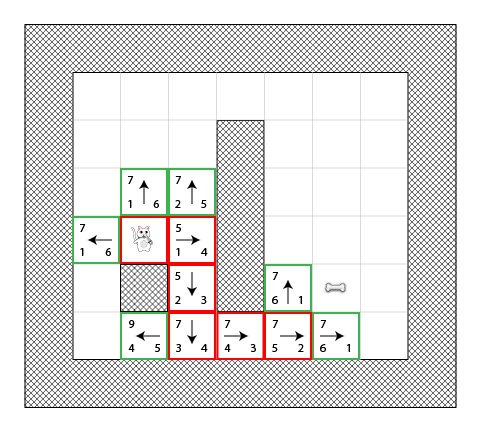
我们差不多到终点了，但是这次你看到有两条到达骨头的最短路径提供给我们选择：

在我们的例子中，有两条最短路径：

•1-2-3-4-5-6

•1-2-3-4-5-7
选择哪一条其实没关系，现在到了真正用代码实现的时候了

第七步

 让我们从其中一块方块，再重复一遍步骤吧：

哈哈，骨头已经收入囊中了！

第八步

 现在目标方块在open列表中了，算法会把它添加到closed列表中：
然后，算法要做的事情就是返回，计算出最终的路径！

部分寻路的关键代码：

void CatSprite::moveToward(const cocos2d::CCPoint &target)
{
	this->stopActionByTag(1);

	CCPoint fromTileCoord = _layer->tileCoordForPosition(this->getPosition()); //出发点是当前猫所在点
	CCPoint toTileCoord = _layer->tileCoordForPosition(target);                //到达的目的点

	float epsion = 0.0000001f;
	//比较下当前点与目标点，看看是不是已经走到了地方
	if(abs(fromTileCoord.x-toTileCoord.x)<epsion && abs(fromTileCoord.y - toTileCoord.y)<epsion) //if(fromTileCoord == toTileCoord)
	{
		CCLog("You're already there");
		return;
	}
	//撞墙了或不可走，播放撞墙声音
	if (!_layer->isValidTileCoord(toTileCoord) || _layer->isWallAtTileCoord(toTileCoord))
	{
		SimpleAudioEngine::sharedEngine()->playEffect("hitWall.wav");
		return;
	}

	CCLOG("From: %f, %f", fromTileCoord.x, fromTileCoord.y);
	CCLOG("To: %f, %f", toTileCoord.x, toTileCoord.y);

	//先清空open表和close表
	bool pathFound = false;
	_spOpenSteps.clear();
	_spClosedSteps.clear();

	//首先添加猫的所在方块到open表里
	this->insertInOpenSteps(ShortestPathStep::createWithPosition(fromTileCoord));

	do 
	{
		// 得到最小的F值步骤
		// 因为是有序列表，第一个步骤总是最小的F值
		ShortestPathStep *currentStep = _spOpenSteps[0];
		currentStep->retain();

		//添加当前步骤到close表里
		_spClosedSteps.push_back(currentStep);

		//将它从Open表里删除
		_spOpenSteps.erase(_spOpenSteps.begin());

		//如果当前步骤是目标方块，就完成了
		if (ToolUtils::isEqualTwoPoint(currentStep->getPosition(), toTileCoord))
		{
			this->constructPathAndStartAnimationFromStep(currentStep); //确立动画路径

			_spOpenSteps.clear();
			_spClosedSteps.clear();
			break;
		}
		//还没到目标，就取出猫周围的邻接块集，一一计算G值并添加到open表
		vector<CCPoint> vecPos = _layer->walkableAdjacentTilesCoordForTileCoord(currentStep->getPosition());
		for (size_t i=0; i<vecPos.size(); ++i)
		{
			ShortestPathStep *step = ShortestPathStep::createWithPosition(vecPos[i]);
			//检查步骤是不是已经在closed列表里
			if(this->getStepIndex(_spClosedSteps, step)!=-1)
				continue;

			//计算从当前步骤到此步骤的代价，一般是1
			int moveCost = this->costToMoveFromStepToAdjacentStep(currentStep, step);

			//检查这个邻接点是否已经在open表里了
			size_t index = this->getStepIndex(_spOpenSteps, step);

			//不在open表里，添加它
			if (index == -1)
			{
				// 设置此邻接点步骤的父节点为当前步骤，作为计算好路径时回溯之用
				step->setParent(currentStep);

				// G值等同于上一步的G值 + 从上一步到达这儿的成本
				step->setGScore(currentStep->getGScore() + moveCost);
				//H值等于从此步到目标的估算值
				step->setHScore(this->computeHScoreFromCoordToCoord(step->getPosition(), toTileCoord));

				//按升序添加到open列表
				this->insertInOpenSteps(step);
			}
			else  //已经在open表里，就需要根据当前步重新计算G值大小，并按升序存入open表
			{
				//获取计算好的step
				step = _spOpenSteps.at(index);

				//检查G值是否低于当前步骤到此步骤的值
				if ((currentStep->getGScore() + moveCost) < step->getGScore())
				{
					step->setGScore(currentStep->getGScore() + moveCost);
					//step因为要先从open表里同删除再按序插入，所以要先扣留它的引用
					step->retain();

					// 因为G值改变了，F值也会跟着改变
					// 所以为了保持open列表有序，需要将此步骤移除，再重新按序插入
					vector<ShortestPathStep*>::iterator it = _spOpenSteps.begin() + index;

					_spOpenSteps.erase(it);

					//重新按序插入
					this->insertInOpenSteps(step);

					step->release();
				}
			}
		}
	} while (_spOpenSteps.size()>0);

	if (_shortestPath.empty())
	{
		SimpleAudioEngine::sharedEngine()->playEffect("hitWall.wav");
	}

}

void CatSprite::insertInOpenSteps(ShortestPathStep *step)
{
	int stepFScore = step->getFScore();
	size_t count = _spOpenSteps.size();

	//搜寻第一个比它大的，插入后面
	std::vector<ShortestPathStep*>::iterator it = _spOpenSteps.begin();
	while(it != _spOpenSteps.end())
	{
		if(stepFScore <= (*it)->getFScore())
			break;
		it++;
	}

	_spOpenSteps.insert(it, step);
}

详细的源代码和示例游戏程序在这里   源代码