Quaternion Screened Poisson Equation for Low-Light Image Enhancement——论文笔记

邱L宁X

于 2023-09-05 13:13:15 发布

阅读量108

点赞数

文章标签：论文阅读

本文链接：https://blog.csdn.net/qiulei0202/article/details/132649903

版权

摘要：

图像增强是一种增强低照度图片照度的方法，它能在增强的同时保持图像的真实度和自然度。对于彩色图像，大多数方法采用分开处理不同彩色通道的方式，但这样会忽略掉不同彩色通道间的联系。因此，本文采用基于四元数（Quaternion）的模型去保留颜色相关性，它可以通过四元数将某一像素的颜色信息整合起来。此外，我们提出了基于伽马校正函数（Gamma-correction function）的正则化器，并将其整合进屏蔽泊松方程（screened Poisson equation）用于图像增强任务。本文分析了模型解的唯一性和存在性。数值结果也证明了我们的方法对于彩色图像增强任务的优越性。

一、引言

图像是人们获取信息的一种重要方式。然而，由于摄影设备的局限性，在夜晚、多云、为避免模糊提升快门速度时，图像容易出现欠曝。在此情况下，图像增强是一种重要的后期处理方式，它通过拉高对比度和照度，以找回低照度图像中的内容信息。

该任务主要应用在彩色图像上，我们注意到，许多增强方法直接将用于处理灰度图的模型用于彩色图像，这很容易导致增强图像颜色通道间的不一致。例如，《Color TV: total variation methods for restoration of vector-valued images》将彩色图像视为三张灰度图的线性组合，并将基于总变分的模型应用在各个灰度图上，而没有考虑颜色通道间的关系。在《Retinex Poisson Equation: a Model for Color Perception》中，Limare 等人将屏蔽泊松方程（screened Poisson equation, SPE）应用于 R、G、B（红色、绿色、蓝色）通道以进行retinex任务，在结果中得到一些颜色噪声。后来，Morel等人将SPE应用于图像增强任务中，它能很好的处理灰度图，但是由于是分别处理彩色图像的R、G、B通道，还是会出现颜色扭曲。这些事实表明，将彩色图像视为三个灰度图的简单组合是不够的，因为忽略了颜色一致性会导致增强图像很容易出现颜色伪影或颜色失真。此外，许多方法试图将图像由RGB色彩空间转为其他色彩空间，例如HSV、YCbCr等。《Enhancement of Color Images by Scaling the DCT Coefficients》提出了一种简单但有效的方法。他们不止是在YCbCr色彩空间中处理亮度分量，同时也处理彩色分量以保留颜色。为了更好地保留颜色信息，《Retinex image enhancement via a learned dictionary》将彩色图像转化为HSV色彩空间。据我们所知，这些方法因此可以处理没有 RGB 通道的彩色图像。然而，处理转换后的通道会忽略通道间的颜色关系，并且带来了增强后颜色的不真实感。

鉴于上述问题，裴和程用纯四元数来表示彩色图像。 $M\times N$ 大小的彩色图像 $u$ 可通过向量 $u= \left [ u_{r} ,u_{g},u_{b}\right ]$ 表示， $u_{r} ,u_{g},u_{b}\in \mathbb{R}^{M\times N}$ 分别为R、G、B通道。通过四元数表示， $u$ 中的每个像素可表示为 $\dot{u}_{pq}= u^r{_{pq}}i+u^g{_{pq}}j+u^b{_{pq}}k$ ， $p=1,2,...,M$ 和 $q=1,2,...,N$ 表示像素的位置， $i,j,k$ 是三个虚数单位。细节将会在第二部分第一节中介绍。将彩色图像表示为向量时，该图像会被分为三张灰度图。而使用四元数来表示每个颜色像素时，颜色信息和跨通道信息将会全部被保留在不可分的四元数值中。考虑到四元数的性质，出现了几个工作将传统的重建模型拓展至四元数领域。他们的工作表明，基于四元数的模型在保留颜色结构上更加有效，这意味将四元数应用至增强彩色图像是具有前景的。

在本文中，我们介绍了一个在SPE（Screened Poisson Equation）基础上建立的基于四元数的图像增强模型。由于正则化器是处理不适定问题的有效工具，我们也将伽马校正扩展至四元数领域作为正则化器。本文贡献总结如下：

提出了基于四元数的增强模型。据我们所在，这是第一个使用纯四元数表示的增强模型。实验结果证明，相较于没有四元数，它在保证自然光照并增强低照度图像上更具优势。
我们提出了一个有效的基于伽马校正的增强正则化器，并将其应用至SPE模型中。实验表明了它对图像增强任务的有效性。
我们推导并给出模型解的理论分析。在模拟图像和真实图像上的实验结果都表明，我们的方法具有更好的性能。

本文剩余部分结构如下。在第二节中，我们回顾了一些关于四元数和SPE的相关工作。在第三节中，给出了并分析了所提出的模型。第四节我们展示了实验来说明我们方法的有效性。在第五节进行了总结。

二、相关工作

在本节中，我们回顾了图像增强任务的四元数理论和屏蔽泊松方程，以促进对所提出的模型的理解。

2.1 四元数理论

四元数首先由Hamilton提出。假定 $\mathbb{H}$ 是一个四元数空间，四元数 $\dot{f}\in \mathbb{H}$ 定义为：

$\dot{f}=f_{0}+f_{1}i+f_{2}j+f_{3}k$ （1）

其中， $f_{0}\in \mathbb{R}$ 是实部， $f_{1},f_{2},f_{3}\in \mathbb{R}$ 是虚部， $i,j,k$ 是虚数单位。当 $f_{0}=0$ 时， $\dot{f}$ 被称为纯四元数。与复数相似，四元数的虚数单位满足 $i^{2}=j^{2}=k^{2}=ijk=-1$ 。然而，虚数单位不满足交换律，但遵循 $ij=-ji=k,jk=-kj=i,ki=-ik=j$ 。

在《A novel block truncation coding of color images using a quaternion-moment-preserving principle》中，四元数被首次引入彩色图像处理。他们发现颜色通道间存在着某种关系。因此，他们将彩色图像的每个像素视为一个整体，而不是将它们分为三个独立的灰度图。因为四元数的虚部有相同的性质，彩色图像 $u\in \mathbb{R}^{M\times N\times 3}$ 的四元数表示为：

$\dot{u}=\begin{bmatrix} \dot{u}_{11},\dot{u}_{12},...,\dot{u}_{1N}\\ \dot{u}_{21},\dot{u}_{22},...,\dot{u}_{2N}\\ ...\\ \dot{u}_{M1},\dot{u}_{M2},...,\dot{u}_{MN}\end{bmatrix}$ （2）

其中， $\dot{u}_{pq}=u^{r}_{pq}i+u^{g}_{pq}j+u^{b}_{pq}k, p=1,2,...,M \textup{and } q=1,2,...,N$ ，这样，彩色图像每个像素都被认作是纯四元数。为了进一步方便计算，《A normalized color difference edge detector based on quaternion representation》提出了一个更好的方式用四元数表示图像。与复数空间相似，他们假设 $\mu =\frac{1}{\sqrt{3}}\left ( i+j+k \right )$ 为单位纯四元数，并且任意与 $\mu$ 相关的单位四元数 $T$ 有如下表示：

$T=\left | T \right |\textup{exp}\left ( \mu \theta \right )=\cos \theta +\mu \sin \theta$ （3）

根据共轭四元数定义： $f^{*}=f_{0}-f_{1}i-f_{2}j-f_{3}k$ ，有：

$\overline{T}=\left | \overline{T }\right |\textup{exp}\left ( \mu^{*} \theta \right )=\cos \theta -\mu \sin \theta$ （4）

对于纯四元数像素 $\dot{v}=v_{r}i+v_{g}j+v_{b}k$ ，有：

$Ti\overline{T}=\left ( \cos \theta +\mu \sin \theta \right )\left ( v_{r}i+v_{g}j+v_{b}k \right )\left ( \cos \theta -\mu \sin \theta \right )\newline \textup{ }= \left [ \dot{v}\cdot \cos 2\theta \right ]+\left [ 2\mu\cdot \left (\mu\cdot \dot{v}\cdot \sin ^{2}\theta \right ) \right ]+\left [ \left (\mu \times \dot{v} \right ) \sin 2\theta\right ]\newline \textup{ }:=\dot{v}^{RGB}+\dot{v}^{B}+\dot{v}^{C}$

在不丧失一般性的情况下，我们设置 $\theta =\frac{\pi }{4}$ 。则纯四元数像素 $\dot{v}$ 可以被表示为 $\dot{v}=\overline{T}\left (\dot{v}^{B}+ \dot{v}^{C} \right )T$ 。因此，对于纯四元数矩阵 $\dot{u}$ ，有：

$\dot{u}=\overline{T}\left (\dot{u}^{B}+ \dot{u}^{C} \right )T$ （5）

请注意，我们将利用等式（5）提出模型。

在此之后，《The Theory of Quaternion Matrix Derivatives》给出了四元数的推导规则。Ell等人提出了基于四元数的快速傅里叶变换（fast Fourier transform, FFT）。随着四元数理论的不断改进，基于四元数的模型已被应用至各种图像处理任务中。然而，大多数工作并没有给出他们模型的理论分析或者解的存在性证明。

2.2 基于屏蔽泊松方程的图像增强

《Retinex Poisson Equation: a Model for Color Perception》提出了一个针对灰度图的对比度增强模型：

$\mathop{min}\limits_{u}\int_{\Omega}\left | \bigtriangledown u- \bigtriangledown f\right |^{2}dx+\lambda \int_{\Omega}\left ( u-f_{m} \right )^{2}dx$ （6）

其中， $u,f\in \mathbb{R}^{M,N}$ 分别为潜在图像和观察到的低照度图像。 $f_{m}$ 是等于图像 $f$ 平均值的图像。 $\lambda$ 是权衡这两个图像的超参数。 $\Omega$ 表示图像域， $\triangledown$ 为梯度算子。公式（6）的解满足如下欧拉方程：

$\lambda \left ( u-f_{m} \right )-\Delta u+\Delta f=0, \textup{over } \Omega$ （7）

其中， $\Delta$ 为拉普拉斯算子。公式（7）可以进一步转化为屏蔽泊松方程，其一般形式定义为：

$\left ( \Delta -\beta ^{2} \right )v=-h$ （8）

其中 $\beta ^{2}=\lambda$ 和 $h=\lambda f_{m}-\Delta f$ 。对于 SPE， $\beta$ 是一个称为“筛选”的常数， $h$ 和 $v$ 可以是实数或复数函数。我们说模型（6）基于 SPE，将（6）称为 SPE 模型。对于（8），可以通过快速傅里叶变换有效地得到解。因此，（6）的解为 $u=\mathcal{F}^{-1}\left ( \frac{-\mathcal{F}\left ( f \right )}{\mathcal{F}(\triangledown )-\beta ^{2}} \right )$ ，其中 $\mathcal{F}\left ( \cdot \right )$ 和 $\mathcal{F}^{-1}\left ( \cdot \right )$ 为傅里叶变换和它的逆。他们的实验证明了SPE在图像增强中的有效性。后来，《Adaptive Variational Model for Contrast Enhancement of Low-Light Images》修改了 SPE 并实现了更好的增强性能。尽管这些方法在灰度图像上表现良好，但由于忽略了颜色通道之间的关系，彩色图像的结果仍然存在颜色失真的问题。为了提高彩色图像增强的性能，本文采用四元数矩阵表示彩色图像。

三、方法

为了实现更好的图像增强效果，我们采用四元数矩阵来表示彩色图像。具体来说，我们使用纯四元数来表示每一个彩色像素值。假定 $\dot{f}$ 是观测到的低照度图像，我们有 $\dot{f}=\bar{T}\left ( \dot{f}^{B} +\dot{f}^{C}\right )T$ ，其中 $T$ 是单位四元数， $\dot{f}^{B}$ 和 $\dot{f}^{C}$ 分别是 $\dot{f}$ 在四元数域的亮度和色度分量。因此，我们的模型 $\dot{J}\left ( \dot{u} \right )$ 为：

$\mathop{min}\limits_{\dot{u}}\int_{\Omega }\left | \bigtriangledown \dot{u}- \bigtriangledown \dot{f}\right |dx+\frac{\lambda }{2}\int_{\Omega }\left ( \dot{u}- \dot{f}_{m}\right )^{2}dx+\frac{\eta }{2}\int_{\Omega }\left ( \dot{u}- \Phi (\dot{f})\right )^{2}dx$ （9）

其中， $\dot{u}=\bar{T}\left ( \dot{u}^{B} +\dot{u}^{C}\right )T$ 为潜在图像， $\dot{f}_{m}=\frac{1}{m}\int_{\Omega }\dot{f}dx$ 为 $\dot{f}$ 的均值， $\Phi \left ( \dot{f} \right )=f^{2\left ( G*\dot{f} \right )}-1$ 是使用伽马校正的粗略增强图像，其中 $G$ 是高斯核。我们提出使用该先验去正则化最后的增强图像。因此，我们将它命名为基于四元数的伽马校正正则化。通过四元数矩阵的导数，我们能够很容易地求解 $\dot{J}\left ( \dot{u} \right )$ 为：

$\left ( \lambda +\eta -\Delta \right )\dot{u}+\Delta \dot{f}-\lambda \dot{f}_{m}-\eta \left [ \Phi \left ( \dot{f} \right ) \right ]^{*}=0$ （10）

其中， $\left ( \cdot \right )^{*}$ 表示四元数共轭。让 $\rho =\lambda +\eta$ 和 $\dot{g}=-\left ( \Delta \dot{f}-\lambda \dot{f}_{m}-\eta \left [ \Phi \left ( \dot{f} \right ) \right ]^{*}=0 \right )$ ，那么公式（10）可以被重新表示为 $\left ( \Delta -\rho \right )\dot{u}=-\dot{g}$ ，这便是基于四元数的SPE。为了给出公式(9)解的存在唯一性，我们在《 $H_{\lambda }$ -regular vector functions and their boundary value problems》之后给出了定义3.1、3.2和3.3。

定义3.1：（四元数函数）

给定一个域 $D\subset \mathbb{R}^{4}$ 以及 $x = \left ( x_{0},x_{1} ,x_{2} ,x_{3} \right )\in D$ ，我们定义一个四元数函数 $\dot{P}:D\rightarrow \mathbb{H}$ 为 $\dot{P}\left ( x \right )=x_{0}+x_{1}i+x_{2}j+x_{3}k$ 。实际上，该四元数方程也可以看做是复数域 $G\supset \mathbb{C}^{2}$ 到四元数域 $\mathbb{H}$ 的映射。其中， $c=\left ( s,t \right )\in G,s=s_{0}+s_{1}i\in \mathbb{C},t=t_{0}+t_{1}i\in \mathbb{C}$ 。因此，该映射可看做为 $\dot{F}\left ( c \right )=s+tj=\left ( s_{0}+ s_{1}i\right )+\left ( t_{0}+ t_{1}i\right )= s_{0}+ s_{1}i+ t_{0}j+ t_{1}k$ 。

定义3.2：

定义 $s$ 和 $t$ 的微分算子分别为：

$\frac{\partial }{\partial s}=\frac{1}{2}\left ( \frac{\partial }{\partial s_{0}} -i\frac{\partial }{\partial s_{1}}\right ),\frac{\partial }{\partial t}=\frac{1}{2}\left ( \frac{\partial }{\partial t_{0}} -i\frac{\partial }{\partial t_{1}}\right )$ （11）

它们的共轭为：

$\frac{\partial }{\partial \bar{s}}=\frac{1}{2}\left ( \frac{\partial }{\partial s_{0}} +i\frac{\partial }{\partial s_{1}}\right ),\frac{\partial }{\partial \bar{t}}=\frac{1}{2}\left ( \frac{\partial }{\partial t_{0}} +i\frac{\partial }{\partial t_{1}}\right )$ （12）

于是，我们有 $\partial _{\dot{F}},\partial _{\bar{\dot{F}}},\partial _{\dot{F}}\partial _{\bar{\dot{F}}},$ 和 $\partial _{\bar{\dot{F}}}\partial _{\dot{F}}$ 为：

${\partial _{\dot{F}}}=2\left ( \frac{\partial }{\partial \bar{s}} +j\frac{\partial }{\partial \bar{t}}\right ),\partial _{\bar{\dot{F}}}=2\left ( \frac{\partial }{\partial s} -j\frac{\partial }{\partial \bar{t}}\right )$ （13）

${\partial _{\dot{F}}}\partial _{\bar{\dot{F}}}=\partial _{\bar{\dot{F}}}{\partial _{\dot{F}}}=4\left ( \frac{\partial^{2} }{\partial s\partial \bar{s}} +\frac{\partial^{2} }{\partial t\partial \bar{t}}\right )=\Delta$ （14）

定义3.3：（四元数正则函数）

如果四元数函数 $\dot{F}\left ( x \right )\in C^{1}\left ( G \right )$ 满足等式 $\partial _{x}F=0$ ，则我们称 $\dot{F}\left ( x \right )$ 是 $G$ 的左正则函数。左正则函数简称为正则函数。

引理3.1：

如果 $\dot{F}\left ( x \right )$ 在 $G$ 中是正则的，那么 $\dot{F}\left ( x \right )$ 的分量函数在G内都是谐波函数。

通过这些定义和复数函数理论， $\dot{J}\left ( \dot{u} \right )$ 的唯一性定理如下：

命题3.1：

假定 $\dot{J}\left ( \dot{u} \right )$ 在 $\Omega$ 中是正则的。如果 $\dot{J}\left ( \dot{u} \right )$ 在非空开集合 $G_{0}\subset \Omega$ 中总是等于0，那么 $\dot{J}\left ( \dot{u} \right )$ 在 $\Omega$ 中总是0。

证明：

我们知道 $\dot{J}\left ( \dot{u} \right )\in C^{1}\left ( \Omega \right )$ 。从公式(10)中，我们知道 $\partial _{\dot{u}}\dot{J}\left ( \dot{u} \right )=0$ 。从定义3.3中可知 $\dot{J}\left ( \dot{u} \right )$ 是非空开集 $G_{0}$ 中的正则函数。根据引理3.1和谐波函数的无限程度可微性， $\dot{J}\left ( \dot{u} \right )\in C^{\infty }\left ( \Omega \right )$ ，则 $\Delta \dot{J}=\partial _{u}\partial _{\dot{u}}\dot{J}=0$ ，所以 $\dot{J}\left ( \dot{u} \right )$ 满足 $\Omega$ 中的拉普拉斯方程，并且 $\dot{J}\left ( \dot{u} \right )$ 中的的每个分量函数为 $G$ 中的谐波函数。因此，如果谐波函数 $\dot{J}\left ( \dot{u} \right )$ 在 $G_{0}$ 中为0，那么它在 $\Omega$ 中也必定为0.

根据命题3.1和 $\partial _{\dot{u}}\dot{J}\left ( \dot{u} \right )$ （10），我们对于模型（9）有唯一解：

$\dot{u}=\frac{\Delta \dot{f}+\lambda \dot{f}_{m}+\eta \left [ \Phi \left ( \dot{f} \right ) \right ]^{*}}{\Delta +\lambda +\eta }$ （15）

四、实验

为了证明所提出方法的有效性，我们将我们的方法与其他增强方法进行比较，包括 SDCT 、SPE 、ALGI、LR3M、BIMEF ，采用配对 LOL 数据集的合成低照度图像和未配对 VV 数据集的真实世界低照度图像。为了验证我们的四元数表示和伽马校正正则化器的有效性，我们还将其与分别去除四元数表示(WithoutQ)和基于四元数的伽马校正正则化(WithoutG)的模型进行了比较。增强的结果由客观数值指标和主观感知质量指标来衡量。

4.1 实验结果：

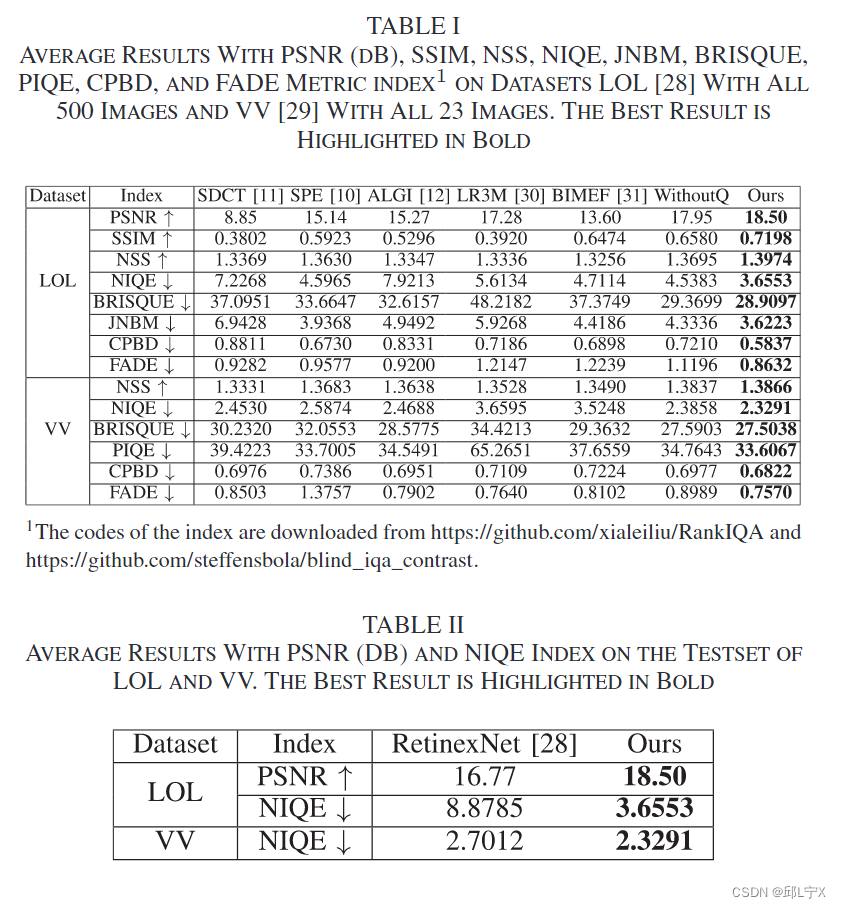
图1和图2展示了增强图像样例。此外，表1列出了数值结果，分别是LOL数据集中500对成对图像和VV数据集中23张未配对图像的平均结果。我们选择代码中给出的默认参数进行方法比较。对于预训练网络，我们将它在LOL数据集上训练。我们在表2中列出了结果。对于我们的模型，超参数是通过试错来选择的，以产生最佳可能结果。具体来说，不同参数的视觉质量和NIQE结果如图3所示。更具体地说，LOL数据集的参数固定为 $\lambda =10$ 和 $\eta =10$ ，VV数据集的为 $\lambda =1$ 和 $\eta =10$ 。

可以看出，本文所提出的方法的结果具有最佳的视觉质量和最佳数值指标。对于图1中SPE的结果，低照度图像中的亮点变为异常值，而其他区域仍然保持相对黑暗。ALGI 的结果将亮点与黑暗进行平均。不利的是，基于学习的方法全局过曝并伴随着颜色失真。相反，非局部方法和变分模型都显示了有限的增强性能。与这些方法相比，没有四元数（WithoutQ）或基于四元数的伽马校正正则化器（WithoutG）的模型在增强性能方面取得了显着的改进。然而，它们都不如图1(i)，其采用四元数表示和基于四元数的伽马校正正则化器，达到最逼真的颜色。对于真实世界的图像，图 2(h) 中我们的方法也有最好的结果。SDCT 和 SPE 的结果显示了光增强效果。相反，ALGI 和 RetinexNet 的结果似乎得到了过度增强。对于WithoutQ模型，可以看到图像失真。表 1和表 2中的数值结果也证明了所提出的方法在增强任务中取得了最佳性能。此外，我们模型的运行时间随图像大小而变化。增强LOL 数据集中大小为 400 × 600 × 3 的图像平均需要 1.52 秒，VV 数据集中大小为 2304 × 1728 × 3 的图像需要 54.65 秒。

4.2 讨论：

最近，基于深度学习的图像增强方法几乎赢得每个人的关注。他们中的大多数都当时取得了最先进的结果。其中，MIRNet提出了并行多尺度卷积流来提取多分辨率特征。KinD是一个经典的分解网络，它在反射分量中引入退化去除以提高质量。DRBN根据监督数据集来重建保真度信号，然后用无监督图像增强结果。SICE从多次曝光图像中学习对比度增强器。GLAD能够计算全局光照并具有全局光照感知，可以更好地处理大范围的光照等级。

显然，所有图像增强网络都实现了显著的低照度图像的视觉质量改进。然而，它们严重依赖大型训练数据集。此外，由于这些方法是黑盒子，因此它们的结果缺乏可解释性。相反，像所提出的基于模型这样的方法没有利用大量的图像进行训练，并且适用于任何给定的图像。结果可以根据任何给定的数据进行调整，其特征具有良好的可解释性。在未来的工作中，我们将将所提出的想法应用于基于学习的模型，并提高彩色图像增强任务的模型的可解释性。

五、结论

本文提出了一个基于四元数的模型用于低照度图像增强，它考虑了不同颜色通道间的内在关系。为提升增强任务的有效性，我们将基于四元数的伽马校正正则化器引入至屏蔽泊松方程中。并进一步基于四元数分析和复变函数理论，分析了模型解的存在性和唯一性。实验证明，本文方法在保留真实颜色的同时实现了最优增强表现。然而，由于本文方法是为了保留颜色信息而设计的，因此，它在彩色图像上具有最优表现，而在包含少量颜色信息的图像上只有次优的表现。未来，我们将采用数据驱动的方法来进一步提升该方法性能。

邱L宁X

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
Quaternion Screened Poisson Equation for Low-Light Image Enhancement——论文笔记

给定一个域以及，我们定义一个四元数函数为。实际上，该四元数方程也可以看做是复数域到四元数域的映射。其中，。因此，该映射可看做为。
复制链接

扫一扫