Hello,各位深度学习炼丹师们!今天咱们要打开激活函数这个神秘的“魔法宝箱”,看看里面都藏着哪些神奇的“法术”,能让我们的神经网络模型像超级赛亚人一样爆发强大威力!
一、为什么需要激活函数?
想象一下,咱的神经网络就像一个超级复杂的“炼丹炉”,输入的数据就像各种药材,一层层地往里扔。要是没有激活函数,这个“炼丹炉”就只是个直来直去的“傻大个”,只能做简单的加减乘除,搞线性运算,根本炼不出啥有魔力的“仙丹”。
激活函数就像是给“炼丹炉”加了一把神奇的“火”,让每一层的数据都能“活”起来,发生非线性的变化。就好比给平淡的药材加了点神奇的催化剂,瞬间让它们产生奇妙的反应。不管多复杂的函数,通过激活函数,神经网络就可以拟合各种曲线,激活函数能让神经网络去逼近,就像给神经网络配备了一把万能钥匙,能打开各种函数曲线的“大门”。
下面就给大家介绍几个神经网络里常用的激活函数。
二、激活函数“大明星”闪亮登场🎉
1. Sigmoid/Logistics 函数:复古的“魔术师”🎩
想象一下,你面前有一堆数字,有的大得像超级火箭,有的小得像蚂蚁。Sigmoid 函数就像一位拥有神奇“压缩魔法”的魔法师,它能把这些数字都变到一个特定的范围里。
它的数学表达式为:

曲线如下图:

x 就是我们要处理的输入数字,e 是一个特殊的常数,大约等于 2.71828。Sigmoid 函数在它定义的所有数字范围内都能算出导数。不过呢,它两边导数会慢慢靠近 0,就像一个“小气鬼”,不太愿意把重要的信息分享出来。当输入的数字 X 特别大或者特别小的时候,这个函数的梯度(也就是斜率)就会变得超级小。在反向传播的过程中,导致了向低层传递的梯度也变得非
常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说, sigmoid 网络
在 5 层之内就会产生梯度消失现象。而且,该激活函数并不是以0为中心的,所以在实践中这种
激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义 Sigmoid 函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 生成一些输入数据
x = np.linspace(-10, 10, 100)
# 计算对应的输出
y = sigmoid(x)
# 绘制 Sigmoid 函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='Sigmoid Function')
plt.xlabel('Input (x)')
plt.ylabel('Output (σ(x))')
plt.title('The Magic of Sigmoid Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 首先,我们导入了numpy库,它就像一个数学小助手,能帮我们进行各种数学运算。还导入了
matplotlib.pyplot库,用来绘制图像。 - 然后,我们定义了
sigmoid函数,就是按照之前说的数学表达式来实现的 - 接着,我们用
np.linspace生成了一组从 -10 到 10 的输入数据,一共 100 个点。 - 计算了这些输入数据对应的 Sigmoid 函数输出值。
- 最后,我们用
matplotlib绘制了 Sigmoid 函数的图像,这样就能直观地看到它是怎么把输入压缩到 0 到 1 之间的啦。
2. tanh(双曲正切曲线):平衡界的“瑜伽大师”🧘
tanh 函数就像一位超厉害的瑜伽大师,追求身体的完美平衡。它能把输入值像做瑜伽动作一样,拉伸到 (−1,1) 之间,而且是以 0 为中心的,就像瑜伽大师站在平衡木中间一样稳。
它的数学表达式:

曲线如下图:

这里面的 e 是一个特殊的常数,大约等于 2.71828。这个公式看起来有点复杂,但其实它就是通过指数运算来巧妙地计算出一个在 -1 到 1 之间的值。就像一个神奇的魔法公式,把输入的 x 变成一个有特定范围的输出。
tanh也是一种非常常见的激活函数。与sigmoid相比,它是以0为中心的,使得其收敛速度要比
sigmoid快,减少迭代次数。然而,从图中可以看出,tanh两侧的导数也为0,同样会造成梯度消
失。若使用时可在隐藏层使用tanh函数,在输出层使用sigmoid函数。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义 tanh 函数
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
# 生成一些输入数据
x = np.linspace(-10, 10, 100)
# 计算对应的输出
y = tanh(x)
# 绘制 tanh 函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='tanh Function')
plt.xlabel('Input (x)')
plt.ylabel('Output (tanh(x))')
plt.title('The Magic of tanh Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 首先,我们导入了
numpy库,它就像一个数学小助手,能帮我们进行各种数学运算。还导入了matplotlib.pyplot库,用来绘制图像。 - 然后,我们定义了
tanh函数,就是按照之前说的数学表达式来实现的。 - 接着,我们用
np.linspace生成了一组从 -10 到 10 的输入数据,一共 100 个点。 - 计算了这些输入数据对应的 tanh 函数输出值。
- 最后,我们用
matplotlib绘制了 tanh 函数的图像,这样就能直观地看到它是怎么把输入压缩到 -1 到 1 之间的啦。
运行这段代码,你就会看到一条像“S”一样的曲线,不过和 Sigmoid 函数的曲线相比,它的输出范围是 -1 到 1。输入值越小,输出越接近 -1;输入值越大,输出越接近 1。
输出结果示例:
我们取几个输入值,看看对应的输出结果:
| 输入值 (x) | 输出值 (tanh(x)) |
|---|---|
| -5 | -0.999909 |
| -2 | -0.964028 |
| 0 | 0 |
| 2 | 0.964028 |
| 5 | 0.999909 |
从表格中可以看到,当输入值为 -5 时,输出值接近 -1;当输入值为 0 时,输出值为 0;当输入值为 5 时,输出值接近 1。这就很好地体现了 tanh 函数输出范围在 -1 到 1 之间的特点。
3. ReLU:豪爽的“江湖大侠”🦸
ReLU全称是Rectified Linear Unit,中文名叫“修正线性单元”。它就像一个简单又高效的“开关”,能让神经网络在处理数据时更加高效和灵活。与一些复杂的激活函数相比,ReLU的计算非常简单,而且在实际应用中表现出了强大的性能。它就像一个勤劳又聪明的小工人,在神经网络里默默地发挥着重要作用。
它的数学表达式:

曲线如下图:

值x大于或等于0时,它就像大侠看到朋友有难,二话不说,输出就是输入本身;输入小于等于 0 时,它就像大侠遇到敌人,直接不理不睬,输出为 0。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义ReLU函数
def relu(x):
return np.maximum(0, x)
# 生成一些输入数据
x = np.linspace(-10, 10, 100)
# 计算对应的输出
y = relu(x)
# 绘制ReLU函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='ReLU Function')
plt.xlabel('Input (x)')
plt.ylabel('Output (ReLU(x))')
plt.title('The Magic of ReLU Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 导入库:我们导入了
numpy库,它就像一个数学小助手,能帮我们进行各种数学运算。还导入了matplotlib.pyplot库,用来绘制图像。 - 定义ReLU函数:使用
np.maximum(0, x)来实现ReLU函数的功能,它会返回输入数组x和0之间的较大值。 - 生成输入数据:用
np.linspace生成了一组从 -10 到 10 的输入数据,一共100个点。 - 计算输出:计算了这些输入数据对应的ReLU函数输出值。
- 绘制图像:用
matplotlib绘制了ReLU函数的图像,这样就能直观地看到它是怎么工作的啦。
运行这段代码,你就会看到一条在x=0处有一个“拐点”的折线。当x<0时,输出为0;当x≥0时,输出随着x的增大而线性增大。
输出结果示例:
我们取几个输入值,看看对应的输出结果:
| 输入值 (x) | 输出值 (ReLU(x)) |
|---|---|
| -5 | 0 |
| -2 | 0 |
| 0 | 0 |
| 2 | 2 |
| 5 | 5 |
从表格中可以看到,当输入值为负数时,输出值都为0;当输入值为0或正数时,输出值就是输入值本身。这很好地体现了ReLU函数的计算规则。
4. LeakReLU:细心的“小跟班”🧑🦯
LeakReLU 函数就像 ReLU 大侠的细心小跟班。
它的公式是:

曲线如下图:

当输入小于等于 0 时,它不像 ReLU 大侠那么绝情,而是会给一个小小的负数输出,就像小跟班在旁边悄悄提醒大侠别忽略小事。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义LeakReLU函数
def leaky_relu(x, alpha=0.01):
return np.where(x >= 0, x, alpha * x)
# 生成一些输入数据
x = np.linspace(-10, 10, 100)
# 计算对应的输出
y = leaky_relu(x)
# 绘制LeakReLU函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='LeakReLU Function ($\alpha = 0.01$)')
plt.xlabel('Input (x)')
plt.ylabel('Output (LeakReLU(x))')
plt.title('The Magic of LeakReLU Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 导入库:我们导入了
numpy库,用于进行各种数学运算;还导入了matplotlib.pyplot库,用来绘制图像。 - 定义LeakReLU函数:使用
np.where函数来实现LeakReLU的功能。当输入数组x中的元素大于或等于0时,返回该元素本身;当元素小于0时,返回该元素乘以斜率α后的值。 - 生成输入数据:用
np.linspace生成了一组从 -10 到 10 的输入数据,一共100个点。 - 计算输出:计算了这些输入数据对应的LeakReLU函数输出值。
- 绘制图像:用
matplotlib绘制了LeakReLU函数的图像,这样就能直观地看到它的工作情况啦。
运行这段代码,你就会看到一条在x=0处有一个“小拐点”的折线。当x<0时,输出为αx,是一条斜率为α的直线;当x≥0时,输出随着x的增大而线性增大。
输出结果示例:
| 输入值 (x) | 输出值 (LeakReLU(x)) |
|---|---|
| -5 | -0.05 |
| -2 | -0.02 |
| 0 | 0 |
| 2 | 2 |
| 5 | 5 |
从表格中可以看到,当输入值为负数时,输出值为输入值乘以斜率后的结果;当输入值为0或正数时,输出值就是输入值本身。这很好地体现了LeakReLU函数的计算规则。
5. SoftMax:多分类界的“皇帝”👑
SoftMax 函数就像多分类界的皇帝,威严又公正。能帮我们将神经网络的输出转化为概率分布,从而轻松判断样本属于各个类别的可能性。
它的公式是:

e 是自然常数,约等于 2.71828。这个公式的含义是,先对输入向量中的每个元素进行指数运算,然后将每个指数运算的结果除以所有元素指数运算结果的和,从而得到一个概率值。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
# 定义SoftMax函数
def softmax(z):
# 防止指数运算溢出,先减去z中的最大值
z_max = np.max(z)
exp_z = np.exp(z - z_max)
sum_exp_z = np.sum(exp_z)
y = exp_z / sum_exp_z
return y
# 生成一个输入向量
z = np.array([2.0, 1.0, 0.1])
# 计算对应的输出
y = softmax(z)
# 打印输出结果
print("输入向量:", z)
print("SoftMax输出:", y)
print("输出概率之和:", np.sum(y))代码解释
- 导入库:我们导入了
numpy库,用于进行各种数学运算。 - 定义SoftMax函数:
- 为了防止指数运算时出现数值溢出的问题,我们先减去输入向量
z中的最大值z_max,这样可以保证指数运算的结果不会过大。 - 然后对减去最大值后的向量进行指数运算,得到
exp_z。 - 计算
exp_z中所有元素的和sum_exp_z。 - 最后将
exp_z中的每个元素除以sum_exp_z,得到SoftMax函数的输出y。
- 为了防止指数运算时出现数值溢出的问题,我们先减去输入向量
- 生成输入向量:我们生成了一个包含三个元素的输入向量
z,分别代表三个类别的原始输出值。 - 计算输出:调用
softmax函数计算输入向量对应的输出。 - 打印结果:打印输入向量、SoftMax输出以及输出概率之和,可以看到输出概率之和为1。
6. Identity:回归界的“透明小精灵”🧚
Identity 函数就像一个透明的小精灵,默默地传递信息。它的公式简单得不能再简单:f(x)=x,输入是什么,输出就原封不动地是什么,就像小精灵不改变任何东西,只是悄悄地帮忙传递。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义Identity激活函数
def identity(x):
return x
# 生成一些输入数据
x = np.linspace(-10, 10, 100)
# 计算对应的输出
y = identity(x)
# 绘制Identity激活函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='Identity Function')
plt.xlabel('Input (x)')
plt.ylabel('Output (Identity(x))')
plt.title('The Simplicity of Identity Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 导入库:我们导入了
numpy库,用于进行各种数学运算;还导入了matplotlib.pyplot库,用来绘制图像。 - 定义Identity激活函数:直接返回输入值
x,实现Identity激活函数的功能。 - 生成输入数据:用
np.linspace生成了一组从 -10 到 10 的输入数据,一共100个点。 - 计算输出:计算了这些输入数据对应的Identity激活函数输出值。
- 绘制图像:用
matplotlib绘制了Identity激活函数的图像,你会看到一条通过原点的直线,斜率为1,这直观地展示了Identity激活函数的线性特性。
运行这段代码,你就能看到一条笔直的直线,清晰地体现了Identity激活函数“输入等于输出”的特点。
输出结果示例:
| 输入值 (x) | 输出值 (Identity(x)) |
|---|---|
| -5 | -5 |
| -2 | -2 |
| 0 | 0 |
| 2 | 2 |
| 5 | 5 |
从表格中可以看到,无论输入值是正数、负数还是0,输出值都和输入值完全相同。这很好地体现了Identity激活函数的计算规则。
7. ELU:优雅的“芭蕾舞者”💃
ELU 函数就像一位优雅的芭蕾舞者,动作流畅又美丽。ELU激活函数是为了解决ReLU激活函数及其变体(如LeakReLU)存在的一些问题而提出的。ReLU函数在输入为负数时,输出为0,这可能导致神经元“死亡”;而LeakReLU虽然给负数输入赋予了一个很小的斜率,但在负数区域仍然是线性的。ELU激活函数在负数区域采用了指数函数的形式,使得它在负数区域具有平滑的曲线,能够更好地处理负数输入,减少神经元“死亡”的可能性,同时还能加速神经网络的收敛速度。
它的公式是:
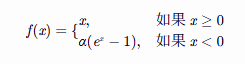
α 是一个正数,通常取值在 0.1 到 1 之间。这个公式的含义是,当输入值x大于或等于0时,输出值就是x本身,和ReLU函数一样;当输入值x小于0时,输出值为α(ex−1),这是一个指数函数减去1后的结果。这样,ELU激活函数在负数区域就有了非线性的特性,并且随着x的减小,输出值逐渐趋近于−α。
下面来看段代码,看看它是怎么工作的吧:
import numpy as np
import matplotlib.pyplot as plt
# 定义ELU函数
def elu(x, alpha=0.1):
return np.where(x >= 0, x, alpha * (np.exp(x) - 1))
# 生成一些输入数据
x = np.linspace(-5, 5, 100)
# 计算对应的输出
y = elu(x)
# 绘制ELU激活函数的图像
plt.figure(figsize=(8, 6))
plt.plot(x, y, label=f'ELU Function ($\alpha = {alpha}$)')
plt.xlabel('Input (x)')
plt.ylabel('Output (ELU(x))')
plt.title('The Power of ELU Function')
plt.grid(True)
plt.legend()
plt.show()代码解释
- 导入库:我们导入了
numpy库,用于进行各种数学运算;还导入了matplotlib.pyplot库,用来绘制图像。 - 定义ELU函数:使用
np.where函数来实现ELU的功能。当输入数组x中的元素大于或等于0时,返回该元素本身;当元素小于0时,返回α(ex−1)的值。 - 生成输入数据:用
np.linspace生成了一组从 -5 到 5 的输入数据,一共100个点。 - 计算输出:计算了这些输入数据对应的ELU激活函数输出值。
- 绘制图像:用
matplotlib绘制了ELU激活函数的图像,这样就能直观地看到它的工作情况啦。
运行这段代码,你就会看到一条在x=0处平滑过渡的曲线。当x≥0时,曲线是一条斜率为1的直线;当x<0时,曲线是一条指数衰减的曲线。
输出结果示例:
| 输入值 (x) | 输出值 (ELU(x)) |
|---|---|
| -5 | -0.99326205 |
| -2 | -0.86466472 |
| 0 | 0 |
| 2 | 2 |
| 5 | 5 |
从表格中可以看到,当输入值为负数时,输出值为α(ex−1)后的结果;当输入值为0或正数时,输出值就是输入值本身。这很好地体现了ELU激活函数的计算规则。
三、激活函数“大比拼”🥊
| 激活函数 | 梯度特性(像不像武功的威力) | 计算复杂度(修炼难度) | 输出范围(攻击范围) | 适用场景(江湖地盘) |
| Sigmoid | 易梯度消失,像武功时灵时不灵 | 低,简单易学 | (0,1),小范围攻击 | 二分类问题输出层(特定老江湖场合) |
| tanh | 仍有梯度消失风险,像偶尔脚滑 | 低,基础招式 | (−1,1),平衡攻击 | 需输出以 0 为中心的隐藏层 |
| ReLU | 梯度稳定(正输入时),像大侠正面出击 | 低,简单粗暴 | [0,+∞),正面大范围攻击 | 大多数隐藏层(负输入多时小心“中暗器”) |
| LeakReLU | 梯度稳定,像小跟班稳稳辅助 | 低,和 ReLU 差不多 | (−∞,+∞),全方位小范围辅助攻击 | ReLU 表现不佳的场景 |
| SoftMax | -,专攻多分类“统治” | 低,专属技能简单 | 概率分布,精准分配“权力” | 多分类问题输出层 |
| Identity | -,默默传递信息 | 低,最简单 | (−∞,+∞),原样传递 | 回归问题输出层 |
| ELU | 较好梯度特性,像舞者灵活舞动 | 中,有点修炼门槛 | (−α,+∞),优雅灵活攻击 | 需良好梯度特性的隐藏层 |
四、总结🎯
在深度学习的炼丹江湖里,选择合适的激活函数就像给我们的模型挑选一件称手的“神兵利器”。二分类问题输出层,Sigmoid 函数这位老江湖偶尔还能露两手;多分类问题输出层,SoftMax 函数这位皇帝稳坐江山;回归问题输出层,Identity 函数这个小精灵默默发挥作用;而隐藏层中,ReLU 及其小伙伴 LeakReLU、ELU 等就像各路武林高手,各有各的绝招,我们要根据具体的“江湖形势”(数据特点和任务需求)来选择最合适的那一位。如果选不好优先选RELU,效果不好选Leaky RELU等。
希望这篇笔记能让你在深度学习的炼丹之路上,像超级炼丹大师一样,轻松驾驭这些激活函数,炼出无敌的模型神丹!💪
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








