李宏毅机器学习课程笔记1：Regression、Error、Gradient Descent

台湾大学李宏毅老师的机器学习课程是一份非常好的ML/DL入门资料，李宏毅老师将课程录像上传到了YouTube，地址：NTUEE ML 2016。 
这篇文章是学习本课程第1-3课所做的笔记和自己的理解。

---

Lecture 1: Regression - Case Study

machine learning 有三个步骤，step 1 是选择 a set of function, 即选择一个 model，step 2 是评价goodness of function，step 3 是选出 best function。

regression 的例子有道琼斯指数预测、自动驾驶中的方向盘角度预测，以及推荐系统中购买可能性的预测。课程中的例子是预测宝可梦进化后的CP值。

一只宝可梦可由5个参数表示，x=(x_cp, x_s, x_hp, x_w, x_h)。我们在选择 model 的时候先选择linear model。接下来评价goodness of function ，它类似于函数的函数，我们输入一个函数，输出的是how bad it is，这就需要定义一个loss function。在所选的model中，随着参数的不同，有着无数个function（即，model确定之后，function是由参数所决定的），每个function都有其loss，选择best function即是选择loss最小的function（参数），求解最优参数的方法可以是gradient descent。

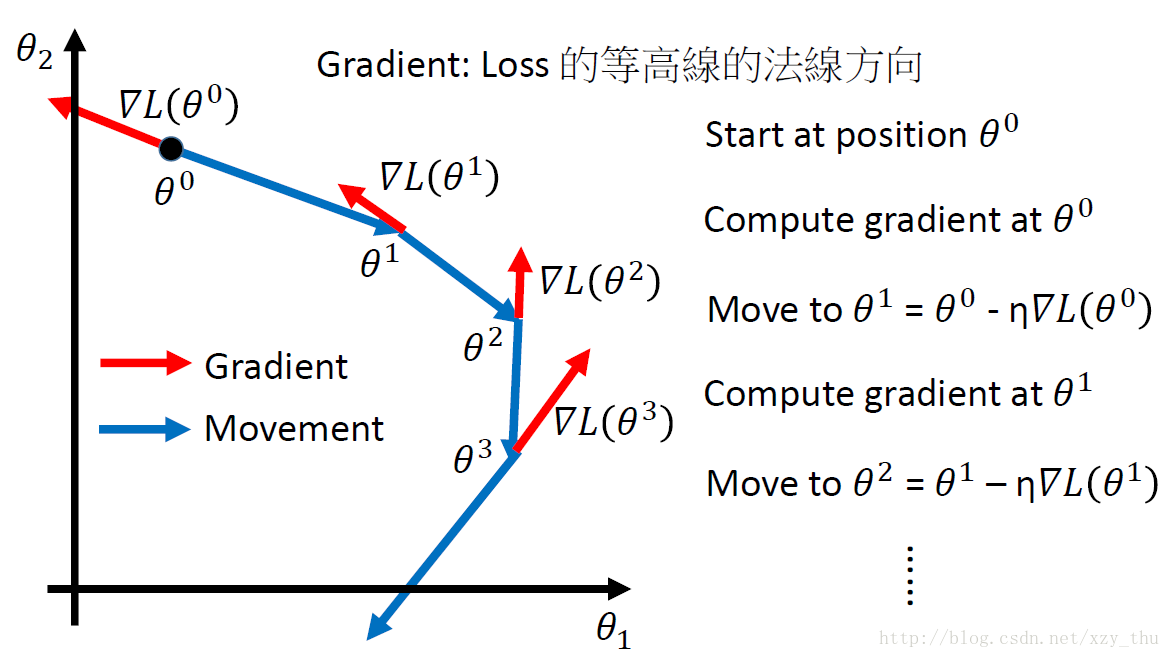
gradient descent 的步骤是：先选择参数的初始值，再向损失函数对参数的负梯度方向迭代更新，learning rate控制步子大小、学习速度。梯度方向是损失函数等高线的法线方向。

gradient descent 可能使参数停在损失函数的局部最小值、导数为0的点、或者导数极小的点处。线性回归中不必担心局部最小值的问题，损失函数是凸的。

在得到best function之后，我们真正在意的是它在testing data上的表现。选择不同的model，会得到不同 的best function，它们在testing data 上有不同表现。复杂模型的model space涵盖了简单模型的model space，因此在training data上的错误率更小，但并不意味着在testing data 上错误率更小。模型太复杂会出现overfitting。

如果我们收集更多宝可梦进化前后的CP值会发现，进化后的CP值不只依赖于进化前的CP值，还有其它的隐藏因素（比如宝可梦所属的物种）。同时考虑进化前CP值x_cp和物种x_s，之前的模型要修改为 
if x_s = pidgey: y = b_1 + w_1 * x_cp 
if x_s = weedle: y = b_2 + w_2 * x_cp 
if x_s = caterpie: y = b_3 + w_3 * x_cp 
if x_s = eevee: y = b_4 + w_4 * x_cp 
这仍是一个线性模型，因为它可以写作 
y = 
b_1 * δ(x_s = pidgey) + w_1 * δ(x_s = pidgey) * x_cp + 
b_2 * δ(x_s = weedle) + w_2 * δ(x_s = weedle) * x_cp + 
b_3 * δ(x_s = caterpie) + w_3 * δ(x_s = caterpie) * x_cp + 
b_4 * δ(x_s = eevee) + w_4 * δ(x_s = eevee) * x_cp 
上式中的粗体项都是linear model y = b + Σw_i * x_i 中的feature x_i。 
这个模型在测试集上有更好的表现。如果同时考虑宝可梦的其它属性，选一个很复杂的模型，结果会overfitting。

对线性模型来讲，希望选出的best function 能 smooth一些，也就是权重系数小一些，因为这样的话，在测试数据受噪声影响时，预测值所受的影响会更小。 
所以在损失函数中加一个正则项 λΣ(w_i)^2。 
越大的λ，对training error考虑得越少。 
我们希望函数smooth，但也不能太smooth。 
调整λ，选择使testing error最小的λ。

Lecture 2: Where does the error come from?

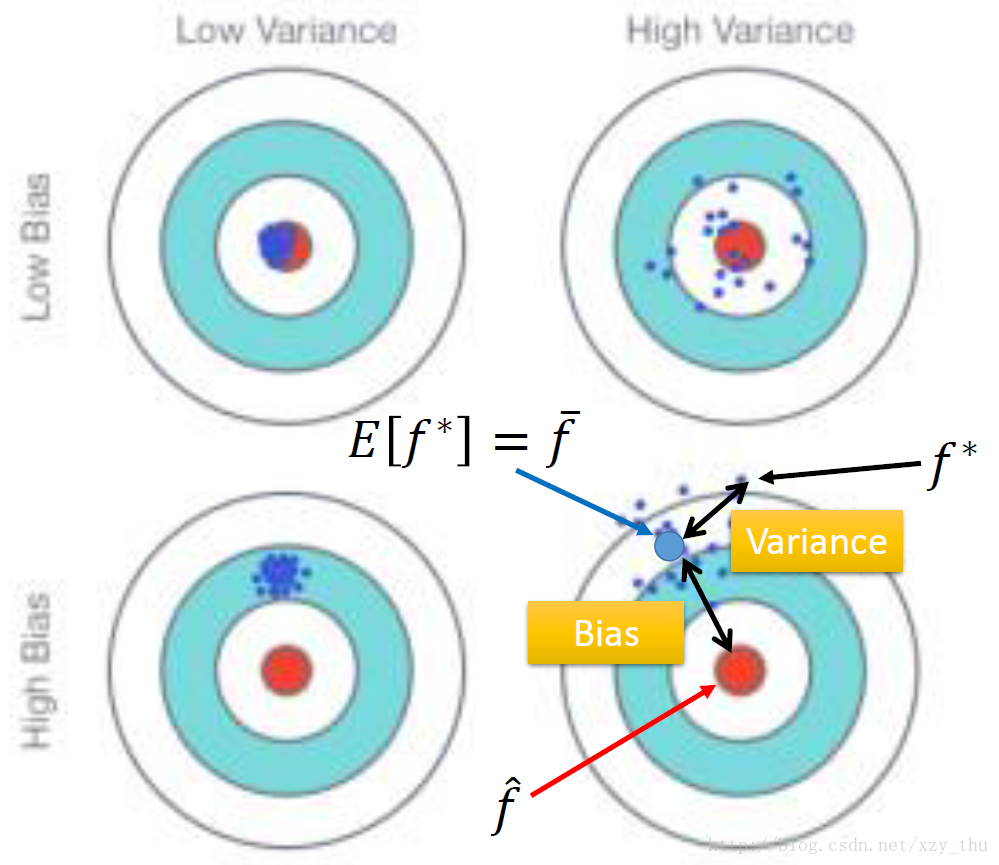
error有两种来源，分别是bias和variance，诊断error的来源，可以挑选适当的方法improve model。

以进化前的宝可梦为输入，以进化后的真实CP值为输出，真实的函数记为 f^ 。（在上帝视角才能知道 f^ ） 
从训练数据，我们找到  f∗ ，  f∗ 是对 f^ 的一个估计。

简单模型，variance小。复杂模型，variance大。（简单模型更少受训练数据影响。复杂模型会尽力去拟合训练数据的变化。） 
bias代表 f¯  与  f^  的距离。简单模型，bias大。复杂模型，bias小。 
simple model的model space较小，可能没有包含target。

在underfitting的情况下，error大部分来自bias。 
在overfitting的情况下，error大部分来自variance。

如果model连训练样本都fit得不好，那就是underfitting, bias大。 
如果model可以fit训练样本，但是testing error大，那就是overfitting, variance大。

在bias大的情况下，需要重新设计model，比如增加更多的feature，或者让model更complex。而此时more data是没有帮助的。 
在variance大的情况下，需要more data，或者regularization。more data指的是，之前100个 f∗ ，每个 f∗ 抓10只宝可梦，现在还是100个 f∗ ，每个 f∗ 抓100只宝可梦。more data很有效，但不一定可行。regularization希望曲线平滑，但它可能伤害bias，造成model space无法包含target  f^ 。

在选择模型时，要考虑两种error的折中，使total error最小。

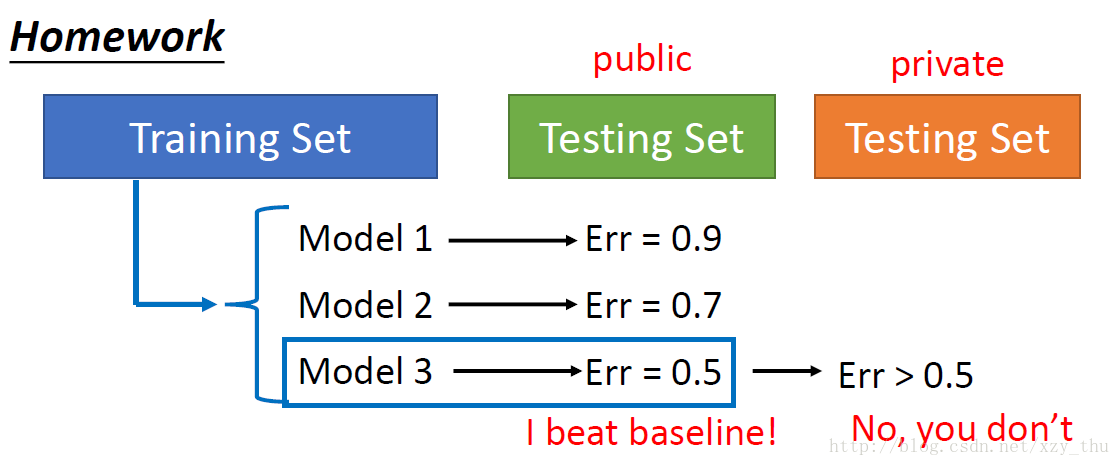
不应该这样做： 

因为这样做，在public testing set上的error rate，并不代表在private testing set上的error rate。 
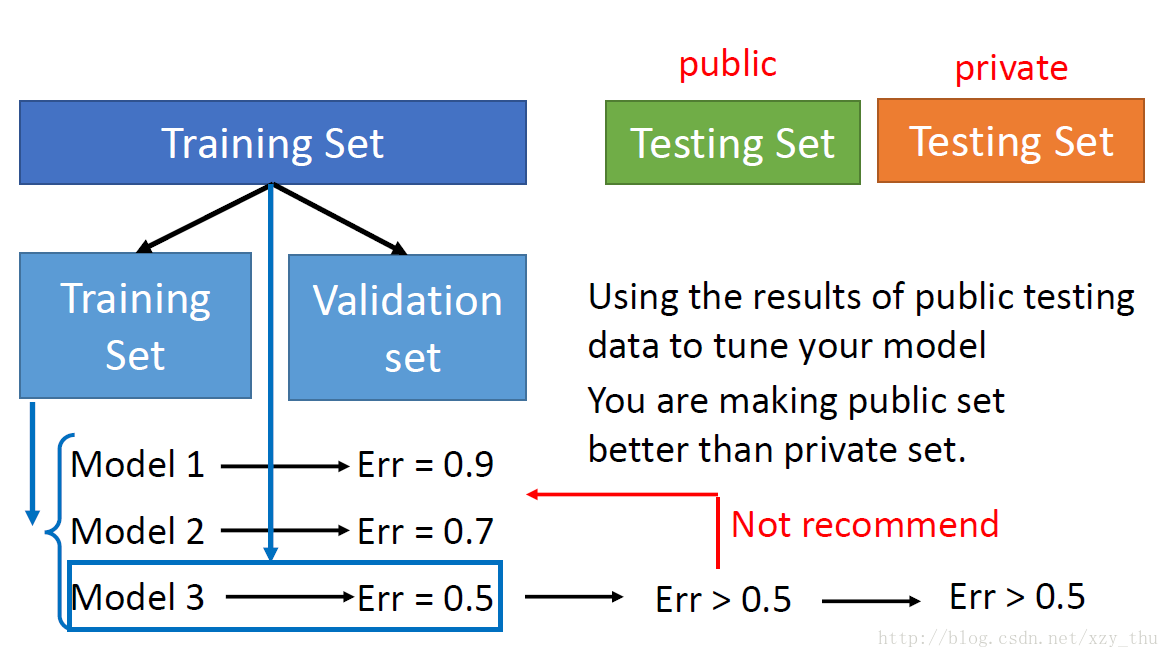
应该采用cross validation的方法！ 

将training set分成training set 和 validation set，在training set上训练model 1-3，选择在validation set 上error rate最小的model。 
如果嫌training set中data少的话，可以在确定model后在全部training data上再train一遍该model。 
这样做，在public testing set上的error rate才会代表在private testing set上的error rate。 
不能用public testing set去调整model。

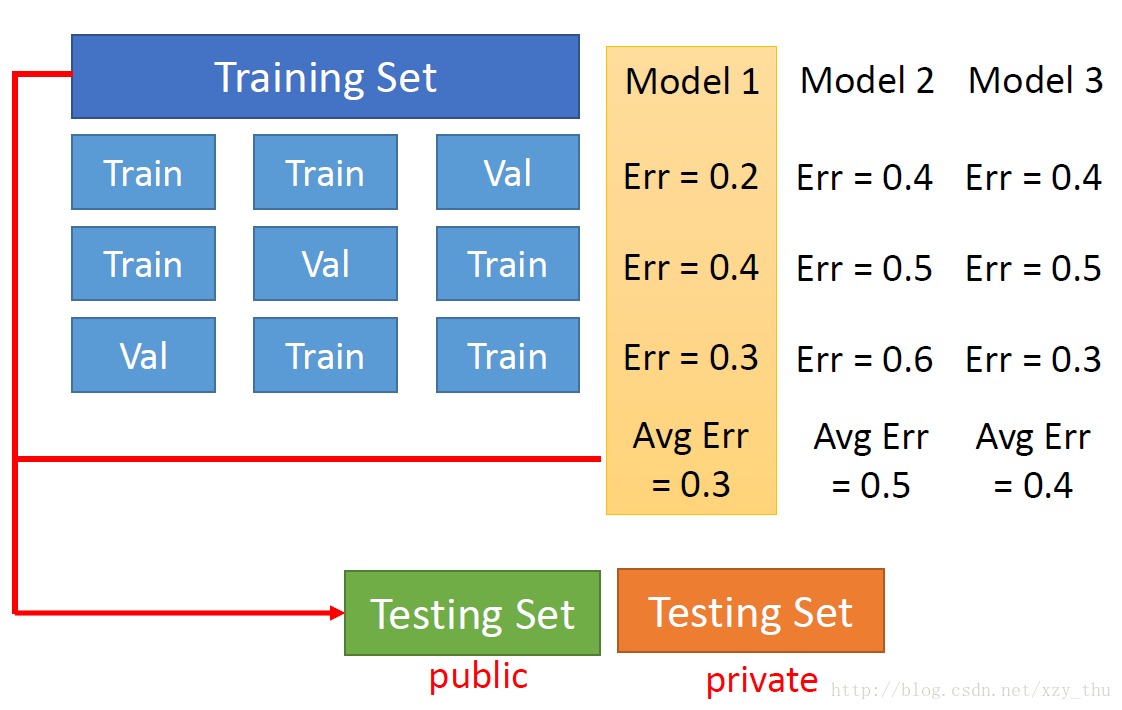
N折交叉验证 

将training set分成N折，每次只有一折作为validation set，其它折作为training set，在各model中选择N次训练得到的N个validation error rate的均值最小的model。

Lecture 3: Gradient Descent

Tip 1: Tuning your learning rates

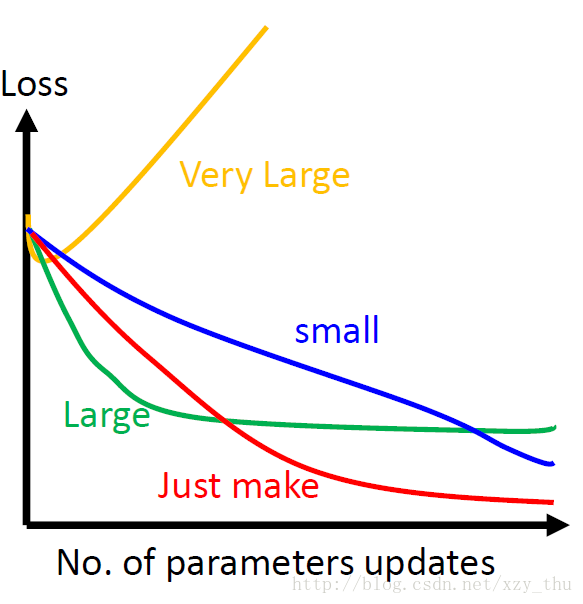
在用梯度下降时要画出loss随更新参数次数的曲线（如下图），看一下前几次更新参数时曲线的走法如何。 

调整学习率的一个思路是：每几个epoch之后就降低学习率（一开始离目标远，所以学习率大些，后来离目标近，学习率就小些），并且不同的参数有不同的学习率。

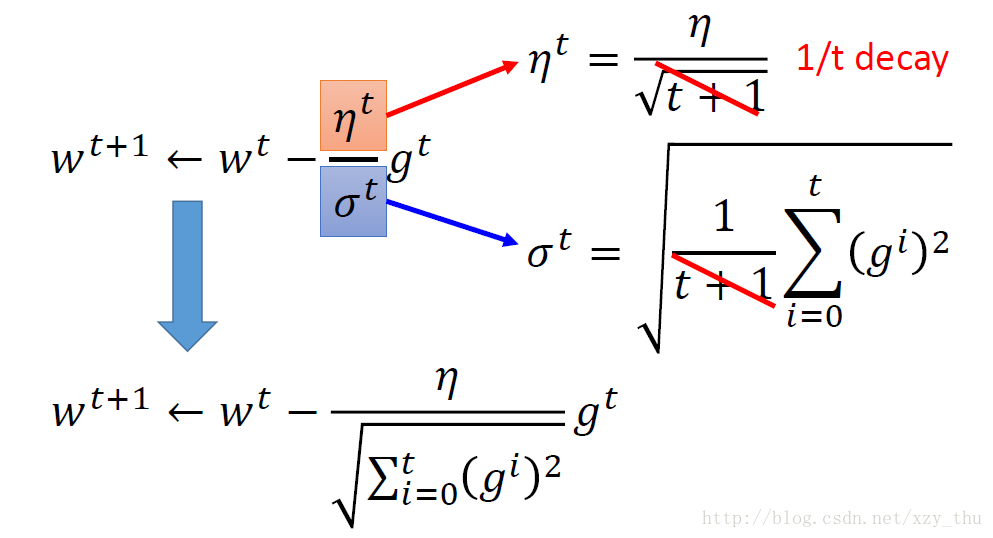
Adagrad

如何理解Adagrad的参数更新式子呢？以一元二次函数为例，参数更新的best step是 

在参数更新式子中， gt  代表first derivative，分母中的根号项反映了second derivative（用first derivative去估计second derivative）。

Tip 2: Stochastic Gradient Descent

SGD让训练过程更快。普通GD是在看到所有样本（训练数据）之后，计算出损失L，再更新参数。而SGD是每看到一个样本就计算出一个损失，然后就更新一次参数。

Tip 3: Feature Scaling

如果不同参数的取值范围大小不同，那么loss函数等高线方向（负梯度方向，参数更新方向）不指向loss最低点。feature scaling让不同参数的取值范围是相同的区间，这样loss函数等高线是一系列共圆心的正圆，更新参数更容易。 
feature scaling的做法是，把input feature的每个维度都标准化（减去该维度特征的均值，除以该维度的标准差）。

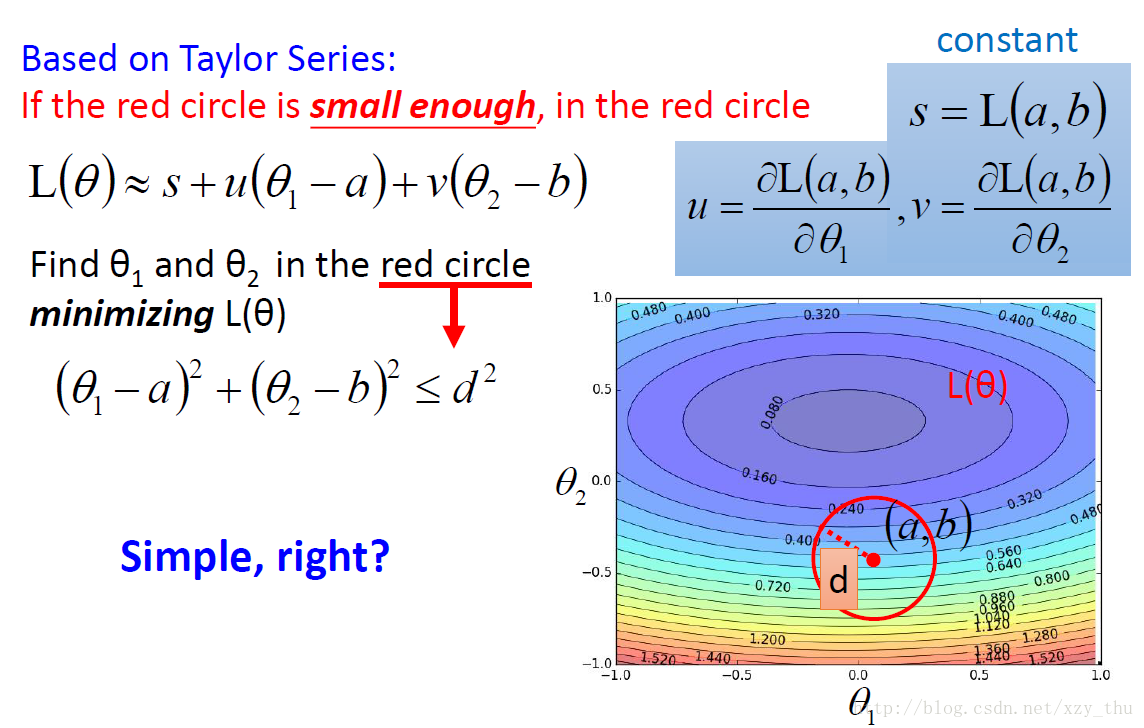
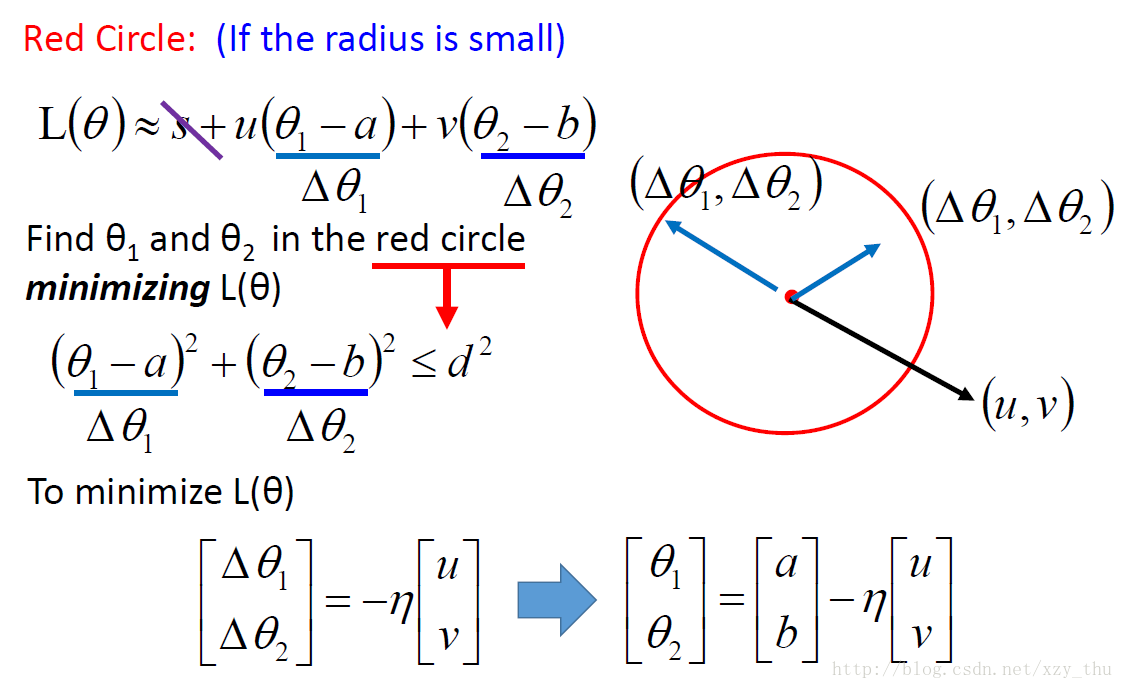
Gradient Descent的理论推导（以两个参数为例）

约等式的成立需要the red circle is small enough这个条件，如果 η  没有设好，这个约等式可能不成立，从而loss不会越来越小。

也可以考虑Taylor Series中的二阶项，要多很多运算，一般不划算。