容斥原理 博弈论（多种Nim游戏解法）

---

容斥原理

容斥原理的简介

容斥原理是组合数学中的一个重要原理，讨论了满足某些条件的元素个数问题。

对于 $n$ 个集合 $A_1,A_2,...A_n$，定义他们的并集包含的元素个数为 $|A_1\cup A_2\cup ...\cup A_n|$，那么根据容斥原理，有：

$|A_1\cup A_2\cup \cdots \cup A_n|$
$=|A_1|+|A_2|+\cdots +|A_n|$
$-|A_1\cap A_2|-\cdots -|A_{n-1}\cap A_n|$
$+|A_1\cap A_2\cap A_3|+\cdots +(-1{)}^{n+1}|A_1\cap A_2\cap \cdots \cap A_n|$

（奇数项为正 偶数项为负）

例如：

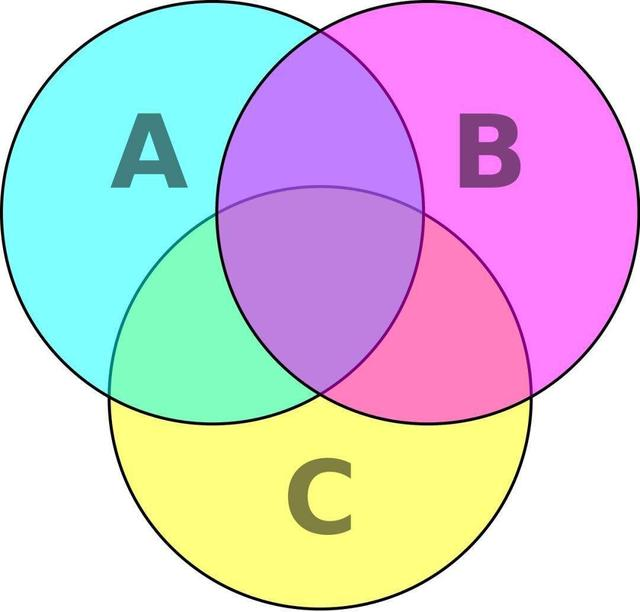
根据上图可得
$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|A\cap C|+|A\cap B\cap C|$

对于 $n$ 个集合 $A_1,A_2,...A_n$，其项数可以表示为 $C_n^1+C_n^2+\cdots +C_n^n$ 通过数学计算可得 $C_n^1+C_n^2+\cdots +C_n^n=2^n-1$，用此再乘以每项的时间复杂度便可以得到整体时间复杂度。

另外也可以通过数学计算得到 $C_n^1-C_n^2+\cdots +(-1{)}^{n-1}{C}_n^n=1$。

能被整除的数（典型例题）

给定一个整数 $n$ 和 $m$ 个不同的质数 $p_1,p_2,\dots ,p_m$。

请你求出 $1$ ~ $n$ 中能被 $p_1,p_2,\dots ,p_m$ 中的至少一个数整除的整数有多少个。

输入格式：
第一行包含整数 $n$ 和 $m$。

第二行包含 $m$ 个质数

输出格式：
输出一个整数，表示满足条件的整数的个数。

数据范围：
$1\le m\le 16$
$1\le n,p_i\le 10^9$

输入样例：

10 2
2 3

输出样例：

7

实现思路

计算 $1$ ~ $n$ 中能被 $p_i$ 一个数整除的整数的方法为 $\lfloor \frac{n}{p_i}\rfloor$。

由于不同质数间存在相同的可被整除的整数情况，这时候直接计算就会导致重叠部分计算多次，因此需要将重复的部分剔除出去，这里使用容斥原理来进行剔除操作。

计算 $1$ ~ $n$ 中能被 $p_i,p_j,p_k$ 多个数整除的整数（类似于重叠部分）的方法为 $\lfloor \frac{n}{p_i\ast p_j\ast p_k}\rfloor$。

将 $m$ 个质数看作 $m$ 个集合， 由于 $m$ 较小，我们可以使用int类型的二进制形式（32 bit）的变量来表示对每个集合的选取情况，1代表选用，0代表未选用。

比如：1110 可看作为选用集合 1 2 3，而集合 0 未选用，这样便可以通过一个int类型遍历来表示当前的集合选用情况。

通过二进制数模拟所有集合选用情况，再利用遍历对二进制数进行解码操作，而后进行正负性相加减便可以得到最终结果。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

const int N = 20;
int p[N];

int main()
{
	int n, m, res = 0;
	cin >> n >> m;
	for (int i = 0; i < m; ++i) cin >> p[i];

	// 模拟对所有集合的每一种选用情况
	for (int i = 1; i < 1 << m; ++i) // 从1开始模拟
	{
		int t = 1, cnt = 0;
		for (int j = 0; j < m; ++j) // 将二进制数所表示的选用情况提取出来（解码）
		{
			if (!(i >> j & 1)) continue;
			if ((long long)t * p[j] > n)
			 // 当质数间的乘积大于n时，对应的质数重叠情况只有0个
			{
				t = -1;
				break;
			}
			t *= p[j];
			cnt++;
		}
		if (t != -1)
		{
			int sign = (cnt & 1) ? 1 : -1; // 判断奇偶性
			res = res + n / t * sign;
		}
	}
	cout << res << endl;
	return 0;
}

时间复杂度：$O(2^m\ast m)$

通过公式 $C_n^1+C_n^2+\cdots +C_n^n=2^n-1$ 可得遍历所有项的时间复杂度为 $O(2^m)$， 对单独一项的时间复杂度为 $O(m)$，这是因为使用二进制数来表示情况，所以需要时间复杂度为 $O(m)$ 的遍历来进行解码操作，提取其中的选取信息。

扩展：用DPS实现

const int N = 20;
int n, m, p[N], res;

// num-代表当前质数乘积 
// cur-代表指向质数数组的指针
// cnt-代表所选用集合的总数
void dfs(int num, int cur, int cnt)
{
	if (cur == m) // 当cur把质数数组都遍历一遍之后代表该种选用情况的结束
	{
		if (cnt) // 排除一个质数都不选的选用情况
		{
			if (cnt % 2) res += n / num;
			else res -= n / num;
		}
		return;
	}
	dfs(num, cur + 1, cnt); // 不选用当前质数的集合
	dfs(num * p[cur], cur + 1, cnt + 1); // 选用当前质数的集合
}
int main()
{
	cin >> n >> m;
	for (int i = 0; i < m; ++i) cin >> p[i];
	dfs(1, 0, 0);
	cout << res << endl;
	return 0;
}

时间复杂度：$O(2^m)$

由于不用二进制数来模拟选取情况，所以也就不需要时间复杂度为 $O(m)$ 的遍历来从二进制数中提取出选取情况的解码操作。

博弈论

博弈论(Game Theory) 是研究 多方参与者 在某种竞争或合作情况下进行的策略选择和相互作用的一门数学理论。它主要研究参与者如何通过各种策略最大化自己的收益。

博弈论中的相关性质

公平组合游戏(Impartial Combinatorial Game, ICG)是组合博弈论中的一个重要概念。

所谓公平组合游戏，是指具有以下特征：

1. 游戏中只有两个玩家，分先手和后手。
2. 两者地位完全对等，有同样的可选行动。
3. 每个位置要么先手必胜，要么后手必胜，不存在平局。
4. 参与者都会采取最优策略。

注：城建棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不符合公平组合游戏。

一些典型的公平组合游戏包括：

• Nim游戏：从几堆物品中拿走任意数量的游戏。
• 威佐夫游戏：在图上移动棋子吃掉对方的游戏。
• 没有后效应的游戏：当前行动不会对之后可行动产生影响。

通过对这类游戏规律的研究，发展出了一套完整的理论体系，建立了组合博弈论这一独立的学科分支。公平组合游戏抽象化地反映了很多现实世界的竞争情况。

博弈论的相关结论

先手必胜状态：

• 在这个游戏状态下，先手玩家有一个必胜策略，可以通过采取相应的游戏行动最终获胜，不论对手如何行动。
• 即先手玩家可以保证自己赢得游戏。这个游戏状态对先手玩家有利。

先手必败状态：

• 在这个游戏状态下，先手玩家无论采取何种行动最终都会输，后手玩家存在必胜策略。
• 即该状态下无论先手玩家如何行动，后手玩家都可以通过相应的行动获取最终的胜利。这个状态对后手玩家有利。
• 后手玩家可以保证自己赢得游戏。

对于NIM游戏，在两名选手都足够聪明，每一步都是最优解的情况下：

$a_1\oplus a_2\oplus \cdots \oplus a_n=0$ 先手必败

$a_1\oplus a_2\oplus \cdots \oplus a_n\ne 0$ 先手必胜

就是把所有堆的石子个数异或起来，结果是零，先手必败，不是零，先手必胜。

先手必败必胜的证明

①当 $a_1\oplus a_2\oplus \cdots \oplus a_n=0$ 时，先手必败：

这个结论实际上是基于一个性质，即对于任意一个非负整数 $x$，有 $x\oplus x=0$。基于这个性质，我们可以证明在这种情况下，先手必败。

假设初始状态下，有 $a_1\oplus a_2\oplus \cdots \oplus a_n=0$。考虑以下情况：

• 如果先手选择 $a_1$，那么剩下的异或和就变为 $(a_2\oplus \cdots \oplus a_n)$。
• 如果先手选择 $a_2$，那么剩下的异或和就变为 $(a_1\oplus a_3\oplus \cdots \oplus a_n)$。
• 以此类推，如果先手选择 $a_i$，剩下的异或和就变为 $(a_1\oplus \cdots \oplus a_{i-1}\oplus a_{i+1}\oplus \cdots \oplus a_n)$。

在这些情况下，无论先手如何选择，剩下的异或和都会变成一个非零值。由于异或满足交换律和结合律，这些选择的结果最终都会导致剩余的异或和为一个非零值。因此，无论先手如何操作，最终的游戏状态都会变为一个不满足条件的状态。

②当 $a_1\oplus a_2\oplus \cdots \oplus a_n\ne 0$ 时，先手必胜：

在这种情况下，异或和不为零。证明先手必胜需要使用归纳法。对于$n=1$的情况，只有一个数，先手直接取走即可。

假设对于 $n=k$，当 $a_1\oplus a_2\oplus \cdots \oplus a_k\ne 0$ 时，先手必胜。现在考虑 $n=k+1$ 的情况。

将 $a_1\oplus a_2\oplus \cdots \oplus a_{k+1}$ 分成两部分：$x=a_1\oplus a_2\oplus \cdots \oplus a_k$ 和 $a_{k+1}$。根据归纳假设，当 $x\ne 0$ 时，先手必胜。此时，先手可以执行以下操作：

• 如果先手选择取走 $a_{k+1}$，那么剩下的异或和变为 $x$，根据归纳假设，先手必胜。
• 如果先手选择取走 $a_i$（$1\le i\le k$），剩下的异或和变为 $x\oplus a_i$。由于 $x\ne 0$，$x\oplus a_i$ 也不为零，那么根据归纳假设，先手也必胜。

因此，无论哪种情况，先手都有必胜策略。综上所述，当 $a_1\oplus a_2\oplus \cdots \oplus a_n\ne 0$ 时，先手必胜。

Nim游戏（典型例题）

题目描述：
给定 $n$ 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式：
第一行包含整数 $n$。

第二行包含 $n$ 个数字，其中第 $i$ 个数字表示第 $i$ 堆石子的数量。

输出格式：
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围：
$1\le n\le 10^5,1\le$每堆石子数$\le 10^9$

输入样例：

2
2 3

输出样例：

Yes

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

int main()
{
	int n, res = 0;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int tmp;
		cin >> tmp;
		res ^= tmp;
	}
	if (res) cout << "Yes" << endl;
	else cout << "No" << endl;
	return 0;
}

台阶-Nim游戏（典型例题）

题目描述：
现在，有一个 $n$ 级台阶的楼梯，每级台阶上都有若干个石子，其中第 $i$ 级台阶上有 $a_i$ 个石子（$i\ge 1$）。

两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。

已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式：
第一行包含整数 $n$。

第二行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 级台阶上的石子数 $a_i$。

输出格式：
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围：
$1\le n\le 10^5,1\le a_i\le 10^9$

输入样例：

3
2 1 3

输出样例：

Yes

实现思路

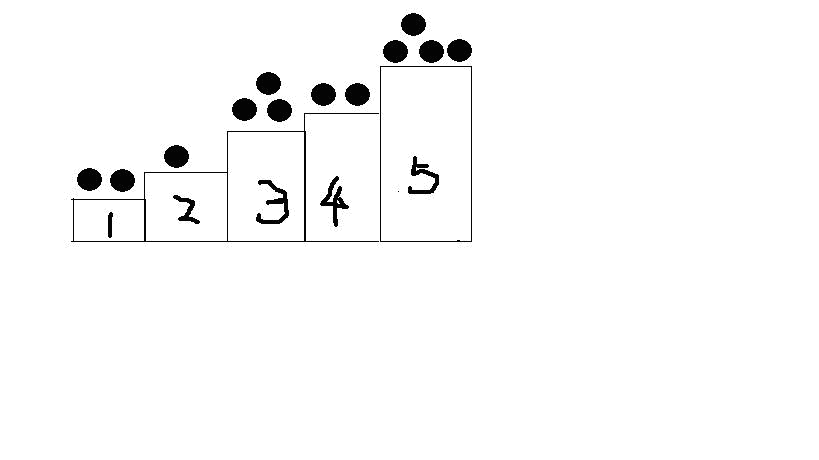
模拟每次只能向下挪动至下一级台阶的行动，我的想法是将高于台阶1的堆分成多个堆，例如图中台阶5的堆，将这个堆分为5份石子数量相等的台阶1的堆，模拟需要至少5次才能将台阶5的堆拿至地面。

因此可以得到： $$\underset{台阶1}{\underbrace{2}}\oplus \underset{台阶2}{\underbrace{1\oplus 1}}\oplus \underset{台阶3}{\underbrace{3\oplus 3\oplus 3}}\oplus \underset{台阶4}{\underbrace{2\oplus 2\oplus 2\oplus 2}}\oplus \underset{台阶5}{\underbrace{4\oplus 4\oplus 4\oplus 4\oplus 4}}$$

由于异或(xor)的特性，相同的数异或等于0，便可以进行优化，当阶数为偶数时，异或结果必定为0，奇数时，异或结果直接就等于台阶上的石子数。

从而可以推导出结论：

• 如果 奇数 阶台阶的石子个数 异或值不是零，则 先手必胜。

• 如果 奇数 阶台阶的石子个数 异或值是零， 则 先手必败。

代码实现

未利用异或特性优化前：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

int main()
{
	int n, res = 0;
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		int tmp, cnt = i;
		cin >> tmp;
		while (cnt--)	res ^= tmp; // 由台阶数分堆
	}
	if (res) cout << "Yes" << endl;
	else cout << "No" << endl;
	return 0;
}

利用异或特性优化后：

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
using namespace std;

int main()
{
	int n, res = 0;
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		int tmp;
		cin >> tmp;
		if (i & 1) res ^= tmp; // 利用异或特性优化
	}
	if (res) cout << "Yes" << endl;
	else cout << "No" << endl;
	return 0;
}

Mex函数与SG函数

有向图游戏的概念：

• 节点和边：有向图游戏由一组节点和连接节点的有向边组成。每个节点表示游戏的一个状态，而有向边表示从一个状态到另一个状态的合法转移。

• 玩家轮流移动：在有向图游戏中，玩家轮流进行移动。每一步玩家可以从当前状态转移到某个后继状态，选择的后继状态必须遵循游戏的规则。

• 游戏终止状态：每个有向图游戏都有终止状态，到达终止状态后游戏结束。终止状态可能是获胜状态或失败状态，这取决于游戏的规则。

• SG 函数和 Mex 函数：SG 函数（Sprague-Grundy 函数）和 Mex 函数是解决有向图游戏的关键工具。SG 函数为每个节点赋予一个非负整数值，表示该节点的状态价值。Mex 函数返回集合中没有出现的最小非负整数。通过 SG 函数和 Mex 函数，可以计算出游戏的最佳策略。

• 必胜策略（先手必胜）和必败策略（先手必败）：在有向图游戏中，存在必胜策略和必败策略。如果一个玩家始终能够采取最佳策略，并且可以确保在有限步内获胜，那么该玩家有必胜策略。相反，如果玩家无论如何都无法避免失败，那么该玩家有必败策略。

• Nim 游戏和其他变体：Nim 游戏是有向图游戏的一个著名例子，它涉及在堆中取石子。还有许多其他变体的有向图游戏，如拈游戏、Grundy’s Game 等。

Mex(Minimum Excluded value)函数，是一个常见的组合游戏和集合论中的概念。它通常用来解决一类博弈问题，其中两个玩家轮流从一个集合中取元素，每次取一个元素，并且不能重复取已经被取走的元素。当某一玩家无法继续操作时，该玩家输掉游戏。

Mex 函数的定义：对于一个给定的非负整数集合，它返回一个非负整数，表示在这个集合中，不属于集合的最小非负整数。

mex ( S ) = min ⁡ { x ∣ x ∈ N 0 , x ∉ S } \text{mex}(S) = \min \{ x \mid x \in \mathbb{N}_0, x \notin S \} mex(S)=min{x∣x∈N0​,x∈/S}

例如：

S = { 0 , 1 , 2 , 4 } ⇒ m e x ( S ) = 3 S=\{0,1,2,4\} ⇒ mex(S)=3 S={0,1,2,4}⇒mex(S)=3

$mex$函数和$sg$函数用于计算有向图游戏的答案，主要思路是:

• $mex$函数返回集合 $S$ 中没有出现的最小非负整数。
• $sg$函数定义为 $sg(n)=mex(sg(i_1),sg(i_2)...)$，其中 $i_1,i_2...$ 是节点 $n$ 的后继节点。
• 对于图 $G$，定义$sg(G)=sg(head)$，其中head是G的头节点。
• 对于 $n$ 个图 $G_1,G_2,...G_n$，它们的$sg$函数值的异或和就是这个有向图游戏的答案。

假设有 $n$ 个独立局面，它们的 $SG$ 值分别为 $sg(G1),sg(G2),...,sg(Gn)$，其中 $G_i$ 表示第 $i$ 个局面。那么整个组合游戏的 $SG$ 值 $sg(G)$ 可以表示为这些局面 $SG$ 值的异或和：

$$sg(G)=sg(G_1)\oplus sg(G_2)\oplus ...\oplus sg(G_n)$$

例如：

以NIM游戏为例，数量为7个石子的一堆，每人抽取轮流只能抽取2或5个石子，不能不抽取，判断先手必胜还是先手必败。

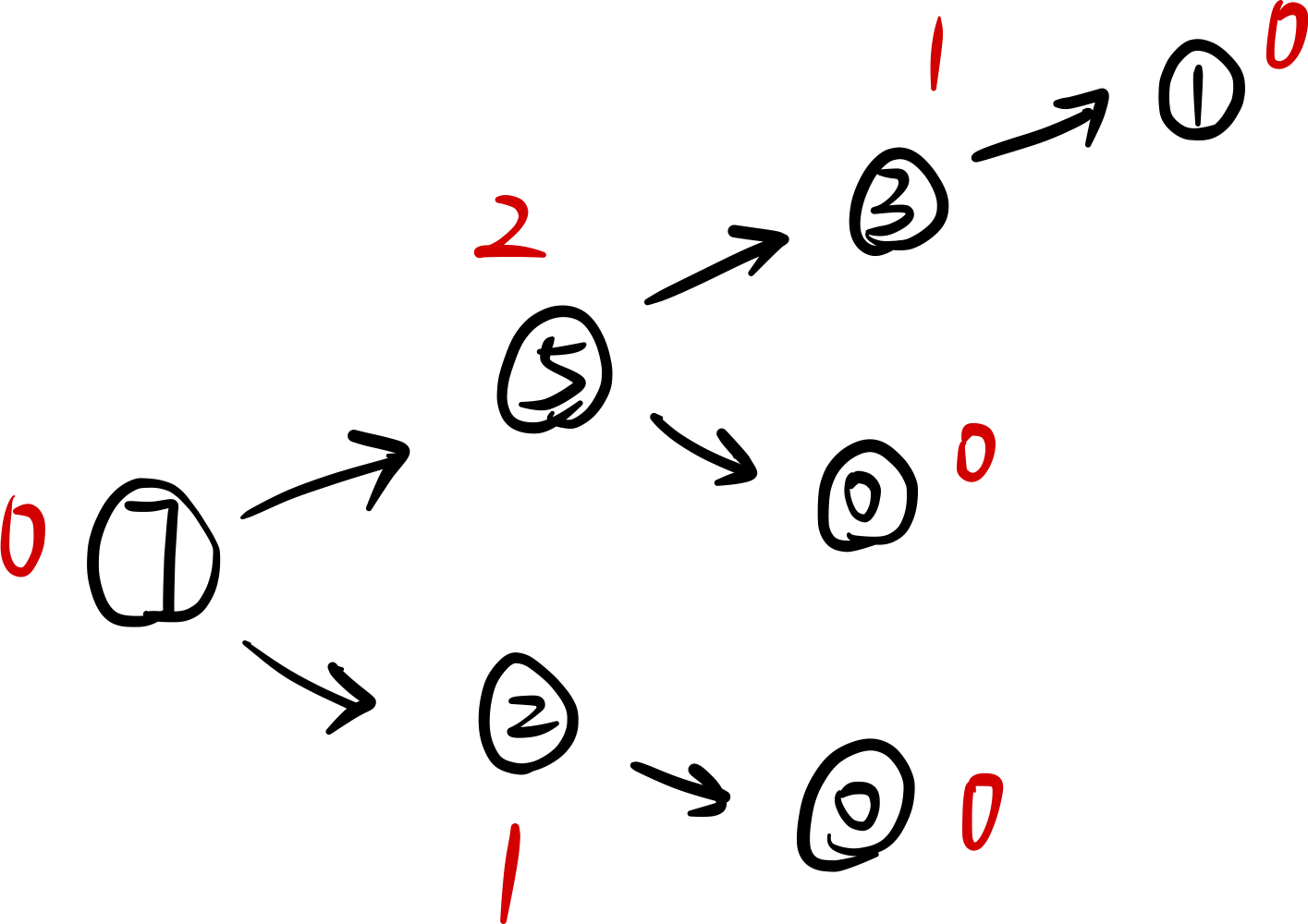
从末尾开始计算，可以得到$sg(head)=0$，由于此时只有一堆，即只存在一个有向图，所以 $sg(head)=0$ 得到结果先手必败。

对多个有向图的情况（例如多个堆的情况），将每个有向图的sg(head)异或到一起，再根据先手必胜必败的条件，得出对应的结论。

对$G_1,G_2,G_3,\dots ,G_n$的 $n$ 个有向图，结论为：

先手必败：
$$sg(G_1)\oplus sg(G_2)\oplus sg(G_3)\oplus \cdots \oplus sg(G_n)=0$$
先手必胜：
$$sg(G_1)\oplus sg(G_2)\oplus sg(G_3)\oplus \cdots \oplus sg(G_n)\ne 0$$

集合-Nim游戏（典型例题）

题目描述：
给定 $n$ 堆石子以及一个由 $k$ 个不同正整数构成的数字集合 $S$。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 $S$，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式：
第一行包含整数 $k$，表示数字集合 $S$ 中数字的个数。

第二行包含 $k$ 个整数，其中第 $i$ 个整数表示数字集合 $S$ 中的第 $i$ 个数 $s_i$。

第三行包含整数 $n$。

第四行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 堆石子的数量 $h_i$。

输出格式：
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围：
$1\le n,k\le 100,1\le s_i,h_i\le 10000$

输入样例：

2
2 3

输出样例：

Yes

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<unordered_set>
using namespace std;

const int N = 110, M = 10010;
int a[N], f[M], k, n;

int sg(int x)
{
	if (~f[x]) return f[x]; // 记忆化搜索：保证每种状态只会被算一次
	unordered_set<int> s; // 用哈希表存储当前节点的集合所存有的非负数的元素
	for (int i = 0; i < k; ++i)
	{
		int num = a[i];
		if (x >= num) s.insert(sg(x - num)); // 将新的状态加进来
	}
	for (int i = 0;; i++) if (!s.count(i)) return f[x] = i; // 找出不存在集合当中的最小值并返回
}
int main()
{
	int res = 0;
	memset(f, -1, sizeof f);
	cin >> k;
	for (int i = 0; i < k; ++i) cin >> a[i];
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int x;
		cin >> x;
		res ^= sg(x); // 求出每堆石子的SG值将其异或
	}
	if (res) cout << "Yes" << endl;
	else cout << "No" << endl;
	return 0;
}

拆分-Nim游戏（典型例题）

题目描述：
给定 $n$ 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆 规模更小 的石子（新堆规模可以为 $0$，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式：
第一行包含整数 $n$。

第二行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 堆石子的数量 $a_i$。

输出格式：
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围：
$1\le n,a_i\le 100$

输入样例：

2
2 3

输出样例：

Yes

实现思路

取走其中的一堆石子，然后放入两堆 规模更小 的石子，相当于将一个局面拆分成了两个局面，由SG函数理论：多个独立局面的SG值，等于这些局面SG值的 异或和。

$$sg(G)=sg(G_1)\oplus sg(G_2)\oplus ...\oplus sg(G_n)$$

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<unordered_set>
using namespace std;

const int N = 110, M = 10010;
int f[N], n;

int sg(int x)
{
	if (~f[x]) return f[x];
	unordered_set<int> s;
	for (int i = 0; i < x; ++i)
	{
		for (int j = 0; j <= i; ++j)
			s.insert(sg(i) ^ sg(j));
	}
	for (int i = 0;; i++) if (!s.count(i)) return f[x] = i;
}
int main()
{
	memset(f, -1, sizeof f);
	cin >> n;
	int res = 0;
	while (n--)
	{
		int x;
		cin >> x;
		res ^= sg(x);
	}
	if (res) cout << "Yes" << endl;
	else cout << "No" << endl;
	return 0;
}