理论--一文了解bspline曲线的理论知识，学会手撸代码

简介：

在规划领域，表达path的方式有离散点，五次多项式，贝塞尔曲线，B样条曲线，螺旋线。作为从业者，掌握一种曲线，对于做轨迹优化是非常有必要的。如果自己想要做一些轨迹优化的项目，能够自己手写一个曲线，还是很有用的。因为搬轮子虽然也可以，但如果如果需要利用曲线特有的性质做一些事儿，就得很了解才行。

B样条曲线性质和代码示例

参考文献：

https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/

1.B样条的优势

天然分段，分段之间是天然C2连续的，这对于运动规划是很好的性质，是分段多项式和分段贝塞尔不具备的性质。
二阶连续的特性，使得B样条在拼接处，只需保持控制点不变，就可达到曲率连续，而对于离散点，很难约束拼接处曲率连续，对于五次多项式，倒是可以，但不如b样条方便。

2.理论知识

$$C(u)=\sum _0^n{N}_{i,p}(u)P_i(2.1)$$
三大元素：基函数$N_{i,p}$，控制点$P_i$，节点向量knot vector U = { u 0 , u 1 , . . . , u m } U = \{u_0,u_1,...,u_m\} U={u0​,u1​,...,um​}

数量关系：控制点个数n+1，节点个数m+1，阶数p，m = n + p + 1

三种类型：open, clamped, closed B-spline curve
曲线起点不过第一个控制点；曲线起点通过第一个控制点；曲线闭合。

2.1 节点向量和基函数

2.1.1 基本概念

有一些概念需要分清楚：

1. p阶bezier曲线：共有p+1个控制点，只有一段轨迹
2. p阶b-spline曲线：控制点不限，最少p+1个，多段C2连续的轨迹（段之间天然C2连续）
3. 分段(peicewise)p阶bezier曲线：控制点不限，多段C2连续的轨迹（段之间C2连续需要边界约束）
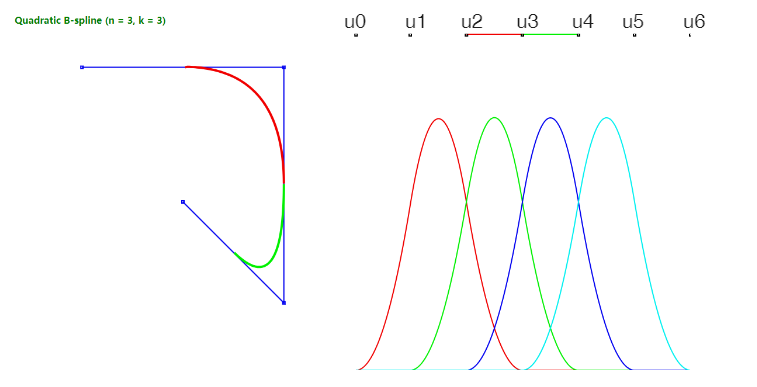
   这里需要搞清楚一个问题，每一小段曲线，由相应的p+1个控制点加相应的p+1个基函数确定，那b-样条曲线是如何自动分段，自动选取相应的相应的基函数和控制点的呢？如下图所示：

1. 红色控制点生成红色曲线，蓝色控制点生成蓝色曲线，其中由p个控制点是重复使用的。
2. $N_{i,p}(u)$是一个关于的分段函数，对于指定的$i$来说，$N_{i,p}$仅在某一段u的取值范围内是非零的，其他都是0。
3. 通过$N_{i,p}$是否为零，达到指定控制点的目的。根据不同的$u$，假设3阶，得到3+1个非零的基函数$N_{i,p},N_{i+1,p},N_{i+2,p},N_{i+3,p}$
4. 对于红色曲线，其曲线方程可以看作：
   $$C(u)=N_{0,3}(u)P_0+N_{1,3}(u)P_1+N_{2,3}(u)P3+N_{3,3}(u)P_3+0\ast P_4+0\ast P_5+0\ast P_6+0\ast P_7...$$
5. 对于蓝色曲线，其曲线方程可以看作：
   $$C(u)=0\ast P_0+N_{1,3}(u)P_1+N_{2,3}(u)P3+N_{3,3}(u)P_3+N_{4,3}{P}_4+0\ast P_5+0\ast P_6+0\ast P_7...$$

2.1.2 节点向量knot vector

在上一节中提到，根据不同的u，可以确定哪几个基函数是非零的，哪些是0。可以直观感受到，$N_{i,p}(u)$是关于u的分段函数，这里的分段，其实就是不同的节点之间的分段。
一些基本名词：

1. 节点向量knot vector: U = { u 0 , u 1 , u 2 , . . . u m } U=\{u_0, u_1, u_2, ... u_m\} U={u0​,u1​,u2​,...um​}
2. 节点knot: $u_i$
3. knot span: $[u_i,u_{i+1})$, 称为第i个knot span
4. 均匀和非均匀: knot span间隔相等则为均匀b样条
5. multiple knot: $u_i=u_{i+1}=...u_{i+k-1},k>1$，即两个或以上重复knot，k称为multiplicity
6. simple knot: 没有相同的knot，则该kont为simple knot

(1) 节点向量生成

本文讨论范围为均匀b样条，因此节点是均匀的，且$u_0<=u_1<=u_2...<=u_m$

节点个数：假设n+1个控制点，p阶，$m=n+p+1$，节点个数为$m+1$

取值范围：$[u_0,u_m]$,常见的是取$u_0=0,u_m=1$，当然也可以任意取值，[0,7]，然后进行归一化即可

(2) open curve和clamped curve

根据knot vector是否满足$u_0=u_1=u_2,...=u_p=0$且$u_{m-p}=u_{m-p+1},...=u_m=1$区分，下边以p=3为例：

open curve

曲线的起点不经过第一个控制点，其节点向量如为$[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]$

clampled curve

曲线起点经过第一个控制点，其节点向量为$[0,0,0,0,0.4,0.5,0.6,1.0,1.0,1.0,1.0]$
原因在后边基函数三角形那里在讲 #三角形

2.1.3 基函数定义

b-spline的基函数，没有明确的公式可以直接计算，只有Cox-de Boor递推形式公式，通过0阶基函数，递推到p阶基函数.

(1) Cox-de Boor递推公式

假设节点向量 U = { 0 , 1 , 2 , 3 , 4 , 5 , 6... } , p = 3 U=\{0,1,2,3,4,5,6...\},p=3 U={0,1,2,3,4,5,6...},p=3

$$N_{i,0}=\{\begin{array}{llccccccc}1& \text{if }{u}_i\le u<u_{i+1}& & & & & & & \\ & & & & & & & & (2.3)\\ 0& \text{otherwise}& & & & & & & \end{array}$$

$$N_{i,p}(u)=\frac{(u-u_i)}{u_{i+p}-u_i}{N}_{i,p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}(u)(2.4)$$

0阶基函数$N_{i,0}$是已知的，是分段函数

$$\begin{array}{rlrlrlrlrlrlrlrlrlr}{N}_{0,0}& & & & & & & & & & & & & & & & & & \\ & & N_{0,1}& & & & & & & & & & & & & & & & \\ N_{1,0}& & & & N_{0,2}& & & & & & & & & & & & & & \\ & & N_{1,1}& & & & N_{0,3}& & & & & & & & & & & & \\ N_{2,0}& & & & N_{1,2}& & & & N_{0,4}& & & & & & & & & & \\ & & N_{2,1}& & & & N_{1,3}& & & & N_{0,5}& & & & & & & & (2.6)\\ N_{3,0}& & & & N_{2,2}& & & & N_{1,4}& & & & & & & & & & \\ & & N_{3,1}& & & & N_{2,3}& & & & & & & & & & & & \\ N_{4,0}& & & & N_{3,2}& & & & & & & & & & & & & & \\ & & N_{4,1}& & & & & & & & & & & & & & & & \\ N_{5,0}& & & & & & & & & & & & & & & & & & \end{array}$$
$N_{i,0}$的是0阶基函数，它是关于$u$的分段函数，只有0阶基函数可以通过判断u所在的knot span来确定其值为1还是0。更高阶(1,2,3…)的基函数只能通过低阶基函数递推计算

• 0阶基函数计算

$$N_{0,0}=\{\begin{array}{ll}1& \text{if }{u}_0\le u<u_1\\ 0& \text{if }{u}_1\le u<u_2\\ 0& \text{if }{u}_2\le u<u_3\\ 0& \text{otherwise}\end{array}(2.7)$$
$$N_{1,0}=\{\begin{array}{ll}1& \text{if }{u}_1\le u<u_2\\ 0& \text{otherwise}(2.8)\end{array}$$

$$N_{2,0}=\{\begin{array}{ll}1& \text{if }{u}_1\le u<u_2\\ 0& \text{otherwise}(2.9)\end{array}$$

$$N_{3,0}=\{\begin{array}{ll}1& \text{if }{u}_1\le u<u_2\\ 0& \text{otherwise}(2.10)\end{array}$$

• 1阶基函数计算

由公式2.4，递推计算$N_i,1$:
$$N_{0,1}(u)=\frac{u-u_0}{u_1-u_0}{N}_{0,0}(u)+\frac{u_2-u}{u_2-u_1}{N}_{1,0}(u)$$

将$u_0=0,u_1=1,u_2=2$带入上式，得到：

$$N_{0,1}(u)=u{N}_{0,0}(u)+(2-u)N_{1,0}(u)$$

当$u\in [0,1)时，N_{0,0}=1,否则为0$，当$u\in [1,2)时，N_{1,0}=1,否则为0$，因此可以得到$N_0,1$的分段函数为：

$$\begin{array}{c}{N}_{0,1}=\{\begin{array}{rlr}u{N}_{0,0}(u)& & 0<=u<1\\ (2-u)N_{1,0}(u)& & 1<=u<2\\ 0& & otherwise\end{array}\end{array}$$
$N_{1,1},N_{2,1},N_{3,1}...同理可得，不再赘述$

• 2阶基函数计算
  同理可以推导出2阶基函数：

$$N_{0,2}(u)=\frac{u-u_0}{u_2-u_0}{N}_{0,1}(u)+\frac{u_3-u}{u_3-u_1}{N}_{1,1}(u)$$
$$N_{0,2}(u)=0.5u{N}_{0,1}(u)+0.5(3-u)N_{1,1}(u)$$
$$\begin{array}{c}{N}_{0,2}=\{\begin{array}{rlr}0.5u{N}_{0,1}(u)& & 0<=u<1\\ 0.5u{N}_{0,1}(u)+0.5(3-u)N_{1,1}(u)& & 1<=u<2\\ 0.5(3-u)N_{1,1}(u)& & 2<=u<3\\ 0& & otherwise\end{array}\end{array}$$

• 3阶基函数计算

https://www.ibiblio.org/e-notes/Splines/basis.html
$$N_{0,3}(u)=\frac{u-u_0}{u_3-u_0}{N}_{0,2}(u)+\frac{u_4-u}{u_4-u_1}{N}_{1,2}(u)$$

总结递推规律如下图所示。
需要注意一个特点，基函数的非零区间，随着阶数增加，逐步增加。

• 如0阶基函数$N_{i,0}$的非零区间为$[u_i,u_{i+1})$
• 1阶基函数$N_{i,1}$的非零区间为$[u_i,u_{i+2})$
• 即p阶基函数$N_{i,p}$的非零区间为$[u_i,u_{i+p+1})$

2.1.4 重要性质

下边性质是非常重要的，想要自己写一个b样条曲线，必须要明白，其中性质2和性质3是写出基函数的关键，必须要理解。

性质1：$N_{i,p}(u)$关于u的是p阶多项式，准确说是分段多项式函数 #性质1

性质2：$N_{i,p}(u)$的非零区间为$[u_i,u_{i+p+1})$ #性质2

以三阶基函数为例，$N_{1,3}$是由$N_{1,2}、N_{2,2}$递推得到，以此类推，$N_{1,0},N_{2,0},N_{3,0},N_{4,0}$是递推的初始值，其u所在区间为$[u_1,u_5)$,该区间即为$N_{1,3}$的非零区间
#三角形1

性质3：任意span $[u_i,u_{i+1})$的非零基函数是：$N_{i-p,p}(u),N_{i-p+1,p}(u),N_{i-p+2,p},...,N_{i,p}(u)$ #性质3
#三角形2
以3次b样条为例，对于任意$u$，如何确定该它属于哪一段b样条，即如何确定哪四个控制点和基函数控制着该段曲线呢，通过下边的三角形可以找到答案
$$C(u)=\sum _0^n{N}_{i,p}(u)P_i$$
假设$u\in [u_3,u_4)$，向右做三角形，如橙色三角形，三角形包含的三阶基函数$N_{0,3},N_{1,3},N_{2,3},N_{3,3}$，即$[u_3,u_4)$上非零3阶基函数只有$N_{0,3},N_{1,3},N_{2,3},N_{3,3}$。

性质4：open curve类型，b样条的有效knot为$[u_p,u_{m-p}]$ #性质4
假设p=3，knot个数为m+1，m=7，则有效knot为$[u_3,u_4)$，如下图所示。

思考一下，如果u取在$[u_0,u_3)$，意味着什么？
由 #三角形2 可知，在$[u_2,u_3)$上，无法找到4个非零基函数，也就无法计算b样条；
另一个解释是，只有在$[u_3,u_4)$，才能使得b样条的二阶导数存在，这个求导性质后边会讲。

性质5：在span $[u_i,u_{i+1})$上，所有非零基函数之和为1 #性质5

性质6：knots的个数为$m+1$，基函数个数=控制点个数=$n+1$，$p$阶，则$m=n+p+1$ #性质6

性质7：在一个multiplicity为k的knot，基函数$N_{i,p}(u)$是 $C^{p-k}$连续的 #性质7

1. 对于simple knot，其multiplicity k = 1.

2. 举个例子，二阶基函数$N_{0,2}$是在$[u_2,u3)$上是$C^1$连续的；

3. 注意到，根据性质2，可知$N_{0,2}(u)$在$[u_0,u_3)$上都是非零的，为什么只有在$[u_2,u_3)$上$C^1$连续呢？这个问题在后边讲完‘两个三角形’后就可以明白 #三角形 先说结论，$N_{0,2},N_{1,2},N_{2,2}$三个基函数加上$P_0,P_1,P_2$三个控制点，共同表示第一段曲线(假设为open curve)。该曲线的u区间为$[u_2,u_3)$。即其实的u并不是$u_0$，而是$u_{0+p}$。

2.2 求值方法（Evalute）

已知控制点和节点向量的情况下，给定u求b样条上的点，即求值(Evalute)操作。De boor算法是一种快速且数值稳定的方法。这里按我理解，b样条求值(Evalute)由三种方式。

2.2.1 de boor算法计算$C(u)$

https://en.wikipedia.org/wiki/De_Boor%27s_algorithm#cite_note-4

de boor算法需要用到一个性质：knot的重复度增加，这个knot对应的非零基函数就会减少，当节点的重复度为$p$时（p阶b样条），将只剩下一个非零基函数，那么$C(u)=N_{i,p}(u)=P_i$。
通过不断插入u，使得u对应的非零基函数只有一个，那对应的控制点就是B样条曲线上的点。(注意这里的控制点，会随着插入knot u而重新生成)。
下边举例说明：

Eigen::Vector3d NonUniformBspline::evaluateDeBoor(double t)
{
  if (t < this->u_(this->p_) || t > this->u_(this->m_ - this->p_))
  {
    if (t < this->u_(this->p_))
      t = this->u_(this->p_);
    if (t > this->u_(this->m_ - this->p_))
      t = this->u_(this->m_ - this->p_);
  }
  // determine which [ui,ui+1] lay in
  int k = this->p_;
  while (true)
  {
    if (this->u_(k + 1) >= t)
      break;
    ++k;
  }
  /* deBoor's alg */
  vector<Eigen::Vector3d> d;
  for (int i = 0; i <= p_; ++i)
  {
    d.push_back(control_points_.row(k - p_ + i));
  }
  for (int r = 1; r <= p_; ++r)
  {
    for (int i = p_; i >= r; --i)
    {
      double alpha = (t - u_[i + k - p_]) / (u_[i + 1 + k - r] - u_[i + k - p_]);
      d[i] = (1 - alpha) * d[i - 1] + alpha * d[i];
    }
  }
  return d[p_];
}

2.2.2 de boor递推公式，求出所有的非零基函数（重点掌握）

确定u所处的knot span，挑选相应的基函数和控制点，根据b样条表达式求出$C(u)$。这里需要用到的时基函数的递推公式。
下边举例说明：

2.2.3 计算矩阵表达形式

带入不同的u和控制点，计算$C(u)$。这里需要推导b样条的矩阵表达形式。

本文讨论的是均匀B样条，即节点矢量沿参数轴均匀等距分布。${\Delta }_i=u_{i+1}-u_i$是一个常数。每一个节点区间$[u_i,u_{i+1})$对应着一段b样条曲线，通过归一化将u归一化到$t\in [0,1]$，可以用整体的u来表示b样条。
1.归一化
$$u=u(t)=(1-t)u_i+t{u}_{i+1},t\in [0,1],i=p,p+1,...n$$

2.分段表达式
$$C_i(t)=C(u(t))=\sum _{j=i-k}^i{P}_j{N}_{j,p}(u(t)),t\in [0,1],i=p,p+1,...n$$
矩阵表达式如下：
$$C_i(t)=\left[\begin{array}{ccccc}1& t& t^2& ...& t^p\end{array}\right]M_p\left[\begin{array}{c}{p}_{i-p}\\ p_{i-p+1}\\ ⋮\\ p_i\end{array}\right],t\in [0,1],i=p,p+1,...n$$
对于二次b样条，$p=2$，系数矩阵为
$$M_2=\left[\begin{array}{ccc}1& 1& 0\\ -2& 2& 0\\ 1& -2& 1\end{array}\right]$$
对于三次b样条，$p=3$，系数矩阵为
$$M_3=\left[\begin{array}{cccc}1& 4& 1& 0\\ -3& 0& 3& 0\\ 3& -6& 3& 0\\ -1& 3& -3& 1\end{array}\right]$$
三次均匀b样条曲线方程的矩阵形式为：
$$C_i(t)=\left[\begin{array}{cccc}1& t& t^2& t^3\end{array}\right]\left[\begin{array}{cccc}1& 4& 1& 0\\ -3& 0& 3& 0\\ 3& -6& 3& 0\\ -1& 3& -3& 1\end{array}\right]\left[\begin{array}{c}{p}_{i-3}\\ p_{i-2}\\ p_{i-1}\\ p_i\end{array}\right],t\in [0,1],i=p,p+1,...n$$
下边举例说明：

Vector2d GetPos(int span_index){
	MatrixXd M3(4,4);
	M3 << -1,  3, -3,  1,
	       3, -6,  3,  0,
	      -3,  0,  3,  0,
	       1,  4,  1,  0;
	
	MatrixXd tm(4,4);
	tm  << tf*tf*tf*tf, tf*tf, tf, 1;
	
	MatrixXd control_points; //记录了所有控制点
	MatrixXd pm(4,2);
	pm = control_points.block(span_index,0,4,2);
	//根据knot span, 从control_points中选取4个控制点
	
	MatrixXd pos = tm*M3*pm;
	return Vector2d(pos(0,0), pos(0,1))；
}

2.3 曲率和求导

2.3.1 曲率计算公式：

$$k=\frac{|x^{{}^{\prime }}{y}^{{}^{\prime \prime }}-y^{{}^{\prime }}{x}^{{}^{\prime \prime }}|}{(x^{{}^{\prime }2}+y^{{}^{\prime }2}{)}^{\frac{3}{2}}}$$
对于b样条来说，假设曲线为2维的，xy坐标系，则$C(u)$是一个二维的点($C(u).x,C(u).y$)。
为了求得曲率，需要求出曲线的一阶$C^{{}^{\prime }}(u)$和二阶导数$C^{{}^{\prime \prime }}(u)$

2.3.2 b样条求导

注：这里不讨论clamped curve，仅讨论open curve
p阶b样条的导数为p-1阶b样条。假设p阶b样条定义为：
$$C(u)=\sum _0^n{N}_{i,p}(u)P_i$$
b样条的三大元素，节点向量，控制点，基函数，下边分别介绍求导后的b样条的三大元素。
新的基函数：
$$\frac{\mathrm{d}}{\mathrm{d}u}{N}_{i,p}(u)=N_{i,p}^{{}^{\prime }}(u)=\frac{p}{u_{i+p}-u_i}{N}_{i,p-1}(u)-\frac{p}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}(u)$$
曲线求导公式：
$$\frac{\mathrm{d}}{\mathrm{d}u}C(u)=C^{{}^{\prime }}(u)=\sum _{i=0}^{n-1}{N}_{i+1,p-1}(u)Q_i$$
新的控制点$Q_i$：
(新的控制点$Q_i$的个数会比旧的控制点$P_i$的个数少一个)
$$Q_i=\frac{p}{u_{i+p+1}-u_{i+1}}(P_{i+1}-P_i),i=0,1,2,...n-1$$

新节点向量：
原始的节点向量去除首和尾的两个节点，得到新的节点向量。

原始的节点向量： { u 0 , u 1 , u 2 , . . . u m } \{u_0,u_1,u_2,...u_m\} {u0​,u1​,u2​,...um​}

新的节点向量： { u 1 , u 2 , . . . u m − 1 } \{u_1,u_2,...u_{m-1}\} {u1​,u2​,...um−1​}

更多内容，请关注公众号 哎嗨人生