Leetcode 1105：填充书架（超详细的解法！！！）

附近的家居城促销，你买回了一直心仪的可调节书架，打算把自己的书都整理到新的书架上。

你把要摆放的书 books 都整理好，叠成一摞：从上往下，第 i 本书的厚度为 books[i][0]，高度为 books[i][1]。

按顺序 将这些书摆放到总宽度为 shelf_width 的书架上。

先选几本书放在书架上（它们的厚度之和小于等于书架的宽度 shelf_width），然后再建一层书架。重复这个过程，直到把所有的书都放在书架上。

需要注意的是，在上述过程的每个步骤中，摆放书的顺序与你整理好的顺序相同。 例如，如果这里有 5 本书，那么可能的一种摆放情况是：第一和第二本书放在第一层书架上，第三本书放在第二层书架上，第四和第五本书放在最后一层书架上。

每一层所摆放的书的最大高度就是这一层书架的层高，书架整体的高度为各层高之和。

以这种方式布置书架，返回书架整体可能的最小高度。

示例：

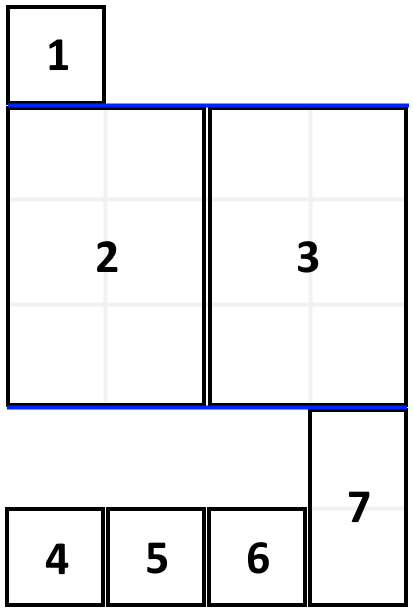
输入：books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelf_width = 4
输出：6
解释：
3 层书架的高度和为 1 + 3 + 2 = 6 。
第 2 本书不必放在第一层书架上。

提示：

• 1 <= books.length <= 1000
• 1 <= books[i][0] <= shelf_width <= 1000
• 1 <= books[i][1] <= 1000

解题思路

典型的动态规划问题啊。我们思考一下子问题，我们定义一个函数f(i)表示放置前i本书的最小高度，那么怎么然这个高度尽量小呢？很容易想到，我们当前的书books[i]要尽量和前面的书放到一排呀！这就是子问题，到底该怎么放呢？知道和前面书的宽度加起来不超过shelf_width，那么我们就可以放。那么转移方程

• $f(i)=min(f(j)+h)$

其中j表示books[j+1:i+1]这几本书可以放到一排，h则表示这些书的最大高度。

class Solution:
    def minHeightShelves(self, books: List[List[int]], shelf_width: int) -> int:
        n = len(books)
        mem = [float("inf")] * (n + 1)
        mem[0] = 0
        
        for i in range(1, n + 1):
            w, h = 0, 0
            for j in range(i-1, -1, -1):
                w += books[j][0]
                h = max(h, books[j][1])
                if w > shelf_width:
                    break
                mem[i] = min(mem[i], mem[j] + h)
        return mem[-1]

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！