机器学习:常用的矩阵向量求导公式

最新推荐文章于 2025-03-04 16:56:16 发布

Rookiekk

最新推荐文章于 2025-03-04 16:56:16 发布

阅读量4.9k

点赞数 6

分类专栏：机器学习中的数学文章标签：机器学习矩阵向量求导

本文链接：https://blog.csdn.net/qq_18888869/article/details/82814258

版权

机器学习中的数学专栏收录该内容

5 篇文章

订阅专栏

学习机器学习的时候有很多线性代数的知识，其中有一些矩阵向量求导的东西不是很熟悉，今天查了很久决定做一个总结。

定义1.梯度（Gradient） [标量对列向量微分]

设 f(x) 是一个变量为的标量函数，其中 $x=(x_{1}...x_{n})^{T}$ 。那么定义 f(x) 对的梯度为 $\frac{\mathrm{d} f(x)}{\mathrm{d} x}$ :

定义2. 海森矩阵（Hessian matrix）[海森矩阵是二阶梯度]

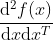设 f(x) 是一个变量为的二阶可微分的标量函数，其中 $x=(x_{1}...x_{n})^{T}$ 。那么定义 f(x) 对的海森矩阵为 $\frac{\mathrm{d} ^{2}f(x)}{\mathrm{d} x\mathrm{d} x^{T}}$ :

海森矩阵是对称阵。

定义3. 雅可比矩阵（Jacobian matrix）[雅可比矩阵本质上是一阶梯度，向量对向量微分]

设 f(x) 是一个K*1的列向量函数

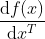其中 $x=(x_{1}...x_{n})^{T}$ 。那么定义 f(x) 对的雅可比矩阵为 $\frac{\mathrm{d} f(x)}{\mathrm{d} x^{T}}$ :

è¿éåå¾çæè¿°

定义4. [矩阵对标量微分]

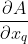$M\times N$ 的矩阵A的元素是一个向量的元素 $x_{q}$ 的函数，定义 $\frac{\partial A}{\partial x_{q}}$ 为：

矩阵的二阶微分：

因为机器学习（这里指的是有监督的机器学习）的一般套路是给定输入X，选择一个模型f作为决策函数，由f(X)预测出Y'。而得到f的参数θ（往往是向量），需要定义一个loss函数（一般都是实值函数），描述当前f预测值Y'与实际的Y值的接近程度。模型学习的过程就是求使得 loss函数 L(f(X),Y)最小的参数θ。这是一个最优化问题，实际应用中都是用和梯度相关的最优化方法，如梯度下降，共轭梯度，拟牛顿法等等。

其实只要掌握上面这个公式，就能搞定很多问题了。

为了方便推导，下面列出一些机器学习中常用的求导公式，其中andrew ng那一套用矩阵迹的方法还是挺不错的，矩阵的迹也是实值的，而一个实数的迹等于其本身，实际工作中可以将loss函数转化成迹，然后在求导，可能会简化推导的步骤。

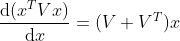证明：二次函数 $f(x) = x^{T}Vx$ ，其中 $x=(x_{1}...x_{n})^{T}$ ， $k\times k$ 矩阵。则 f(x) 对 $k\times 1$ 的列向量的微分为: $\frac{\mathrm{d} (x^{T}Vx)}{\mathrm{d} x} = (V+V^{T})x$ ,以 k=3 的情况举例说明：