浅探Winograd量化

原文链接：浅探Winograd量化 | Hey~YaHei!

上一篇文章《Winograd卷积原理 | Hey~YaHei!》已经介绍过Winograd卷积的基本原理，但终究是理论上的推导，在实际应用的时候其实有些耐人寻味的地方：数学推导假设的是无限的精度和数值范围，但实际计算机的运算精度与数值范围都是有限的，不过按照论文《Fast algorithms for convolutional neural(CVPR2016)》的报告，Winograd在浮点运算上的表现都不错：

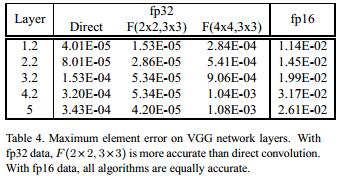
• $F(2\times 2,3\times 3)$的fp32精度损失甚至比Direct Convolution还小，这主要得益于乘法次数的减少，以及简单的变换矩阵（没有非常大或者非常小的数值）
• $F(4\times 4,3\times 3)$的fp32精度损失就比较大了，但似乎也还能接受
• fp16精度损失这三者表现的差不多

浮点运算的Winograd确实不错，但它却似乎也没那么轻易能套上量化——整型可没有浮点这么大的动态范围，如何保证运算过程整型不会溢出将是个令人头疼的问题。

溢出

假设将网络量化成int8，int8的权重和int8的输入，那么得益于int8 * int8，无论是Direct Convolution还是im2col+GEMM，这都能带来可观的加速。但在Winograd里可就不是这么回事了！
注意：im2col也没有对数值的大小进行变换

$F(2,3)$

回顾一下$F(2,3)$的变换矩阵：
$$B^T=\left[\begin{array}{rrrr}1& 0& -1& 0\\ 0& 1& 1& 0\\ 0& -1& 1& 0\\ 0& 1& 0& -1\end{array}\right],G=\left[\begin{array}{rrr}1& 0& 0\\ \frac{1}{2}& \frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& -\frac{1}{2}& \frac{1}{2}\\ 0& 0& 1\end{array}\right],A^T=\left[\begin{array}{rrrr}1& 1& 1& 0\\ 0& 1& -1& -1\end{array}\right]$$
g = [ g 0 g 1 g