一个小的UGM的Demo

翻译自【https://www.cs.ubc.ca/~schmidtm/Software/UGM/small.html】

在这个demo中，我们使用一个非常简单的无向图模型（UGM）来表示一个简单的概率场景，来说明怎样把模型应用于无向图中，怎样在模型里实现解码，推理以及采样。

学生作弊案

这里有四个学生需要做两场多项选择的测试，Cathy,Heather,Mark和Allison。第一场测试中，四名学生被分在了不同的房间。由于Heather和Alllison平时学习认真，因此在这场测试中获得了90%的正确率；而学习不认真的Cathy和Mark则只有25%的准确率。

我们可以假设，学生答对某个题目的概率是和该题无关的（学生答题准确率并非因为题目难度不同，Allison和Heather也并没有因为平时总是一起学习而犯下相同的错误）。如果我们假设在该情况下有100道独立的题目，那么结果有可能如下所示：

这里每一行代表一个题目，每一列代表学生中的某一个，从左到右顺序分别是Cathy(1)，Heather(2)，Mark(3)和Allison(4)。蓝色表示答案正确，红色表示答案错误。

在第二场考试中，这四名学生被分到了同一个考场。座位顺序为Cathy-Heather-Mark-Allison，相邻的学生之间可以看到彼此的答案。Cathy和Mark认为Allison和Heather认真准备了该厂考试（确实如此），Allison和Heather认为Cathy和Mark也认真学习了（实际上并没有），因此，每个人都认为身边的同学的答案都可能是正确的。下面是我们为该模型构建的图：

由于每个人都可以看见自己临近同学的答案，并且认为该答案包含了一些和该问题相关的信息，因此，该学生的答案不再独立，有了依赖。世界死啊好难过，所有学生的答案都是相互依赖的。尽管Mark和Cathy并不相邻，但是由于他们都坐在Heather附近，因此他们的答案也是相互历来的，因此在图中存在这一条连接这两个节点的路径。在UGMs中，我们说，如果两个节点中存在一条路径，那么这两个变量就是互相依赖的。因此在当前问题中（实际上在很多实际应用中），没有变量是独立的。

但是，尽管没有一个变量是独立的，但是问题中仍然存在条件独立性。比如，如果我们知道了Heather的答案作为给定条件，那么Mark和Cathy的答案会独立于这个给定的信息。在UGMs中，如果我们移除了某个条件变量之后这两个变量互相独立，那么我们说两个变量是条件独立的。在当前问题中，我们移除了Heather这个节点之后，Mark和Cathy之间就再无关联了。

成对的无向图模型

考虑到上文所述依赖和条件依赖，我们使用成对的UGM构建一个模型。

在成对的UGMs中，对于某个特定任务中的所有变量x_i的联合概率可以使用一组非负势函数的归一化乘积来表示如下：

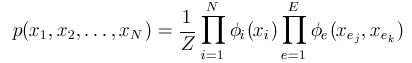
对于每一个节点i，和每一条边e，都有一个势函数。在该例中，节点表示独立的学生（‘Cathy’,‘Heather’,‘Mark’,‘Allison’），在相邻节点之间则定义了边连接(‘Cathy-Heather’,‘Heather-Mark’,‘Mark-Allison’)。注意，这里仅在有直接连接的节点之间设置了边，通过中间变量进行连接的节点之间没有边连接。

节点势函数${\varphi }_i$，对于每一个随机变量$X_i$的可能值都给出了一个非负的权值。比如我们可以设定${\varphi }_i{(}^{\prime }wron{g}^{\prime })=0.75$，${\varphi }_i{(}^{\prime }righ{t}^{\prime })=0.25$，这表示节点1为‘wrong’的状态的相比于为‘right’的状态有着更高的势。同样，边势函数${\varphi }_e$给出了对于边$X_{e_j}$和$X_{e_k}$的所有组合的非负权重。比如在上述案例中，相邻的学生之间有着更高的可能性会给出相同的答案，因此，当$X_{e_j}$和$X_{e_k}$相同时我们会给出该边更大的势。

归一化常数项$Z$是个标量值，使得该联合概率分布和为1，即

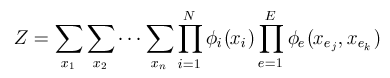
该归一化常数项保证了模型定义了一个有效的概率分布。

给定了图结构和势，UGM包含了三个任务的函数：
1.Decoding解码：找到有着最高概率的变量联合配置
2.Inference推理：计算归一化项$Z$，以及每种状态下每个变量的概率
3.Sampling采样：根据概率分布生成每个变量的联合配置

UGM同样也包括了参数

估计函数，计算势的任务能够最大化数据集的似然。后面的demo中会对其进行介绍，本demo中我们假设势函数已经给定。

边结构

在使用任何UGM姐都的第一步都是定义边结构，因为边结构保存了图结构的信息。为了生成边结构，我们简单将该函数命名为UGM_makeEdgeStruct，有两个参数：邻接矩阵以及每个变量的状态数。在该案例中，我们有4个节点，每个节点有两种状态(‘right’和’wrong’)。邻接矩阵为对称矩阵，如果节点i和节点j之间有连接的话，那么矩阵中的元素(i,j)值置为1。在Matlab里，我们定义边缘结构如下：

//construct the edgeStruct
nNodes = 4;
nStates = 2;
adj = zeros(nNodes,nNodes);
adj(1,2) = 1;
adj(2,1) = 1;
adj(2,3) = 1;
adj(3,2) = 1;
adj(3,4) = 1;
adj(4,3) = 1;
edgeStruct = UGM_makeEdgeStruct(adj,nStates);

edgeStruct的定义是为了解决以下三个问题：
1.通过edgeStruct.nStates查找一个节点的关联状态数
2.通过edgeStruct.edgeEnds查找一条边关联的所有节点
3.通过UGM_getEdges查找一个节点关联的所有边
edgeStruct.nStates是一个简单矢量，用于表示每个节点的状态数。在该案例中，该矢量表示为：

//状态矢量
edgeStruct.nStates
ans =
    2
    2
    2
    2

即每个节点都有两种状态。

edgeStruct.edgeEnds矩阵是一个边数x2的矩阵，每一行给出了每条边的两个节点。在该案例中，该矩阵表示如下：

edgeStruct.edgeEnds
ans =
     1     2
     2     3
     3     4

指定边2，可以获得与其相关的节点，即

edge = 2;
edgeStruct.edgeEnds(edge,:)
ans =
     2     3

函数UGM_getEdges使用edgeStruct.V 和edgeStruct.E矢量指针来快速实现相反操作。即我们可以根据给定节点来找到与其相连的边：

n = 3;
edges = UGM_getEdges(n,edgeStruct)
edges =
     2
     3

由上述说明，我们可以使用下述操作来获得某个节点的相邻节点：

nodes = edgeStruct.edgeEnds(edges,:);
nodes(nodes ~= n)
ans =
     2
     4

上述说明和节点3相邻的节点是2和4。

nodePot

在无向图模型中，节点势是存储在一个nNodes x nStates的矩阵中的，该矩阵叫做nodePot。

edgePot

UGM代码中使用一个nStates x nStates的矩阵来表示边势函数，该矩阵叫做edgePot。对于每条边，edgePot给出了一个nStates x nStates的表格来说明两个节点的状态混合表示。在该案例中，我们认为相邻的两个节点有着相同状态的势是不同状态的势的两倍，如下：

n1\n2	right	wrong
right	2/6	1/6
wrong	1/6	1/6

和节点势类似，我们可以对其进行全局归一化，将其写为如下形式：

maxState = max(edgeStruct.nStates);
edgePot = zeros(maxState,maxState,edgeStruct.nEdges);
for e = 1:edgeStruct.nEdges
   edgePot(:,:,e) = [2 1 ; 1 2]; 
end

Decoding

decoding任务是找到最有可能的配置。
对应于表格中的prodPot列里最大的值。即根据几个势能够得到的具有最大概率的节点状态排列。这个最大概率是通过对于所有排列进行归一化计算所得的。

Inference

inference任务则是找到归一化常量Z，以及独立节点为某个独立状态时的边界概率。

比如，我们这里定义一个inference任务为计算Mark得到正确答案的频率（how often）？第一次测试中，这个数值为25%。在第二次测试中，我们将所有Mark答案正确的排列的prodPot值相加然后除以Z来进行归一化。这里得到的值为0.49/因此，Mark在测试2中得到正确答案的概率是测试1中的将近2倍。Cathy也一样，她的边界概率增长到0.36。她没能达到和Mark一样大的增长是因为她只有一个学霸邻居，同理，Allison和Heather的边界概率均有所下降。

这里我们需要理解decoding和inference的区别。在decoding的计算中，四人最可能的答案排列中，Mark是得到了正确的答案，但是，在inference中，我们知道，Mark是有51%的概率出错的。这说明，最可能的结果排列可能并不总是和最可能出现的状态一致的。