数值优化学习——wolfe条件里的线搜索算法

最新推荐文章于 2024-03-07 14:15:16 发布
VIP文章 最新推荐文章于 2024-03-07 14:15:16 发布
阅读量1.5w 收藏 24
点赞数 4
分类专栏： 算法基础 文章标签： 优化
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_22201697/article/details/69890748
版权

翻译自numerical optimization Chapter3 Line Search Methods
【没写完，可参考http://blog.csdn.net/fangqingan_java/article/details/46405669】
Wolfe条件（或强Wolfe条件）是广泛使用并且较为有效的终止条件。

下面描述一个一维的线搜索过程，该过程确保对于给定的任意参数c1，c2（1>c2>c>0），能够找到一个能够满足强Wolfe条件的步长。 首先，我们假设方向p是下降方向，函数f沿着该方向在下面是有界的。

算法分为两个步骤，第一步首先开始于一个对于步长α的估计值α1，然后后续不断扩大其大小，直到找到一个合适的步长或者一个包含目标步长的区间。如果是后者的话（找到区间），就需要不断调用第二步，称为zoom的函数，来不断缩小区间大小，直到找到合适步长。

line search算法的一个形式说明如下。公式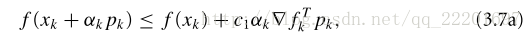这里写图片描述为足够的下降条件，公式

最低0.47元/天 解锁文章
没有头像的宝宝
关注
  • 4
    点赞
  • 踩
  • 24
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
MATLAB 最优化算法合集
05-06
matlab最优化程序包括：无约束一维极值问题、进退法、黄金分割法、斐波那契法、牛顿法基本牛顿法、全局牛顿法、割线法、抛物线法、三次插值法、可接受搜索法、Goidstein法、Wolfe Powell法、单纯形搜索法、Powell法、最速下降法、共轭梯度法、牛顿法、修正牛顿法、拟牛顿法、信赖域法、显式最速下降法、Rosen梯度投影法、罚函数法、外点罚函数法、內点罚函数法、混合罚函数法、乘子法、G－N法、修正G－N法、L－M法、线性规划、单纯形法、修正单纯形法、大M法、变量有界单纯形法、整数规划、割平面法、分支定界法、0-1规划、二次规划、拉格朗曰法、起作用集算法、路径跟踪法、粒子群优化算法、基本粒子群算法、带压缩因子的粒子群算法、权重改进的粒子群算法、线性递减权重法、自适应权重法、随机权重法、变学习因子的粒子群算法、同步变化的学习因子、异步变化的学习因子、二阶粒子群算法、二阶振荡粒子群算法 (matlab optimization process includes Non-binding one-dimensional extremum problems Advance and retreat method Golden Section Fibonacci method of basic Newton s method Newton s method Newton s Law of the global secant method parabola method acceptable to the three interpolation search method Goidstein France Wolfe.Powell France Simplex search method Powell steepest descent method Conjugate gradient method Newton s method Newton s method to amend Quasi-Newton Method trust region method explicitly steepest descent method, Rosen gradient projection method Penalty function method outside the penalty function method within the penalty function method Mixed penalty function multiplier method G-N was amended in G-N method L-M method Of linear programming simplex method, revised simplex method Big M method variables bounded simplex method, Cutting Plane Method integer programming branch and bound method 0-1 programming quadratic programming )
最优化算法wolfe搜索
06-04
本程序为matlab编写的最优化一维搜索方法wolfe
不精确一维搜索：Armijo-Goldstein准则&Wolfe-Powell准则
最新发布
try_trying_try的博客
03-07 644
line search（一维搜索，或线搜索）：精确；不精确(Armijo-Goldstein准则 ＆ Wolfe-Powell准则)的下降量不够充分，以至于算法无法收敛到极小值点，必须引入一些更合理的线搜索准则来。为了解决这个问题，Wolfe-Powell准则应运而生。为了防止迭代过程中函数值。
Wolfe线搜索下一类新的结构拟牛顿算法
07-09
将结构正割法应用到拟牛顿算法中,利用目标函数的梯度信息和函数值信息,引入拟牛顿方程,采用Wolfe线搜索准则,给出了求解无约束优化问题的一个新算法,并在一定条件下证明了新算法的收敛性和超线性收敛性。
Griewank_solve(1)_线搜索案例_优化算法_
09-30
使用线搜索求函数的局部最小值，线搜索的条件是Wolfe 条件
数值最优化第三章线搜索方法
10-19
数值最优化课程中，第三章，线搜索方法知识点讲解，部分证明过程已略去
Armijo条件，Wolfe条件，Goldstein条件
muyuu的博客
09-04 5028
目录线搜索非精确线搜索（Armijo条件，Wolfe条件，Goldstein条件）强Wolfe条件线搜索算法 线搜索 对于迭代式xk+1=xk+αpkx_{k+1} = x_k +\alpha p_kxk+1​=xk​+αpk​，其中pkp_kpk​是由梯度法，牛顿法，CG法等方法计算出的下降方向，α\alphaα是下降的步长。 寻找最优值α=min⁡αf(xk+αpk)\alpha = {\underset {\alpha}{\operatorname {min} }} f(x_k + \alpha p
Armijo线搜索
热门推荐
u011584941的专栏
09-01 2万+
用“人话”解释不精确线搜索中的Armijo-Goldstein准则及Wolfe-Powell准则 line search（一维搜索，或线搜索）是最优化（Optimization）算法中的一个基础步骤/算法。它可以分为精确的一维搜索以及不精确的一维搜索两大类。 在本文中，我想用“人话”解释一下不精确的一维搜索的两大准则：Armijo-Goldstein准则 ＆ Wolfe-Powell准
线搜索weak wolfe条件与Armijo条件
weixin_44623330的博客
07-24 298
见：https://zhuanlan.zhihu.com/p/118443321。与weak wolfe条件的区别就在与曲率设置了绝对值的要求，可以抑制震荡。、结束条件：当梯度值过小。适用性强，收敛速率慢。
数值计算之 线搜索法，Armijo，Wolfe，Goldstein条件，回溯法
qq_41035283的博客
12-19 4899
数值计算之 线搜索法，Wolfe conditions前言梯度法的步长线搜索法非精确线搜索法Armijo条件Wolfe条件Goldstein条件回溯法后记 前言 本篇是基于梯度的优化方法的补充篇 梯度法的步长 梯度下降法、牛顿法、拟牛顿法的主要目的都是求出增量方向。求出增量方向后，如果使用固定步长进行更新，当步长太大导致优化函数与其泰勒展开偏差太大时，可能出现优化函数不降反增的情况，导致迭代不收敛。 因此在获得增量方向后，还需要确定迭代的步长。常用的方法是线搜索法。 线搜索法 线搜索法在求出优化函数f(x)
基于二阶矩阵的最优化问题（二）（附matlab代码）
qq_42035274的博客
05-31 1779
基于二阶矩阵的优化问题（二）非精确搜索确定步长沃尔夫（wolfe）条件Armijo条件曲率下降条件强沃尔夫（wolfe）条件Goldstein条件回溯法（backtracking） 非精确搜索确定步长 在之前的文章中，我们已经讨论了如何从XkX_kXk​更新到Xk+1X_{k+1}Xk+1​，这篇文章我们主要不精确搜索中确定步长的方法 沃尔夫（wolfe）条件 wolfe条件分为Armijo条件和曲率下降条件，只要函数f有下界，所求的α就满足wolfe和强wolfe条件。 Armijo条件 Armijo条件
不精确一维搜索wolfe算法
06-10
不精确一维搜索wolfe算法。C++环境编译
最速下降法 （wolfe）
11-07
Wolfe 条件下的最速下降法的matlab程序
Wolfe线搜索充分下降的修正DY共轭梯度法
07-09
基于DY和DL共轭梯度法,给出一个新的βk公式,在...基于新参数公式建立了采用Wolfe线搜索的共轭梯度算法,证明了算法满足充分下降性和全局收敛性,初步的数值试验结果表明该方法是有效的,适合于求解非线性无约束优化问题.
MATLAB语言书写的优化算法代码
03-12
代码较全，目录如下MATLAB最优化算法集合 1 一、无约束一维极值问题 2 1、进退法 2 2、黄金分割法 3 3、斐波那契法 5 4、牛顿法 7 5、割线法 9 6、抛物线法 10 7、三次插值法 11 8、Goldstein法 13 9、Wolfe-Powell...
一类新的带线搜索的非单调自适应信赖域算法
05-26
对无约束最优化问题提出了一类新的带线搜索的非单调自适应信赖域算法.新算法采用自适应技术,当试验步不成功时,不重解信赖域子问题,而采用Wolfe线搜索,故相对于原有的算法减少了计算量.并在适当的条件下,证明了算法的...
梯度算法大合集——程序实现7种常用的梯度优化算法、5种线搜索方法，并与Pytorch的torch.optim对比结果
06-03
梯度下降法是最著名的优化算法之一，本文基于Python和Pytorch编写了梯度优化程序Gradient_optim，并将...3.可选择的一维线搜索法：黄金分割法、Armijo准则、强Wolfe条件等； 4.动态减小回溯系数/步长最大值/学习率。
最优化 一维不精确搜索wolfe matlab
06-10
就是 最优化教材 上面wolfe准则的不精确一维搜索。完全是书上的步骤。还有一个计算梯度的子程序grad。
Frank-Wolfe算法 matlab程序.zip
03-30
Frank-Wolfe算法 matlab程序(Frank-Wolfe （matlab）)
满足Wolfe条件的线搜索算法的MATLAB例程
06-08
以下是一个简单的MATLAB例程，演示了如何实现满足Wolfe条件的线搜索算法： ```matlab function [alpha, num_evals] = wolfe_search(f, g, x, p, alpha_init) % Set the initial values of alpha and other constants alpha = alpha_init; c1 = 1e-4; c2 = 0.9; max_evals = 100; num_evals = 0; % Evaluate the objective function and its gradient at the starting point f0 = f(x); g0 = g(x); % Loop until the Wolfe conditions are satisfied or the maximum number of % evaluations is reached while num_evals < max_evals % Evaluate the objective function and its gradient at the new point f1 = f(x + alpha*p); g1 = g(x + alpha*p); % Check the Armijo condition if f1 > f0 + c1*alpha*g0'*p break; end % Check the curvature condition if g1'*p < c2*g0'*p break; end % If both conditions are satisfied, return the current alpha value alpha_prev = alpha; alpha = 0.5*(alpha + alpha_init); num_evals = num_evals + 1; end % Return the number of function evaluations used if num_evals == max_evals fprintf('Maximum number of function evaluations reached\n'); end end ``` 该例程采用了传统的回溯线搜索算法，在每次迭代中计算一个新的alpha值，然后检查是否满足Armijo条件和曲率条件。如果两个条件都得到满足，就返回当前的alpha值。如果没有满足，则将alpha值减半并继续迭代，直到达到最大迭代次数或满足条件为止。 请注意，此代码仅为演示目的。在实际应用中，您可能需要根据您的需求进行修改。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值