多项式回归2（Polynomial regression）

1、有了特征，构造出多项式特征，常用工具：PolynomialFeatures（）

#生成由所有多项式组合组成的新特征矩阵度小于或等于指定度的特性的
#如：[a, b]的二次多项式特征为[1,a, b, a^2, ab, b^2]
#PolynomialFeatures(degree=2, interaction_only=False, include_bias=True, order='C')，默认degree是2
from sklearn.preprocessing import PolynomialFeatures
a = [[3, 4], 
     [2, 3]]  
model = PolynomialFeatures(include_bias=False)#为1的那列没了，否则有一列1作为偏置项
b = model.fit_transform(a)
print(b)
'''
[[ 3.  4.  9. 12. 16.]
 [ 2.  3.  4.  6.  9.]]
'''
mode2 = PolynomialFeatures(interaction_only=True)#各自平方项没了，只有交叉项和偏置项,2*3=6,3*4=12
c = mode2.fit_transform(a)
print(c)
'''
[[ 1.  3.  4. 12.]
 [ 1.  2.  3.  6.]]
'''

2、使用多项式回归预测矩阵面积

2.1问题描述

假定现在你知道矩形的面积公式，而不知道求解梯形的面积公式，且同时你手上有若干个类似下图的梯形块儿。已知上底和下底，并且上底均等于高。现在让你建立一个模型，当给定一个上述梯形时你能近似的给出其面积。该如何建模呢？

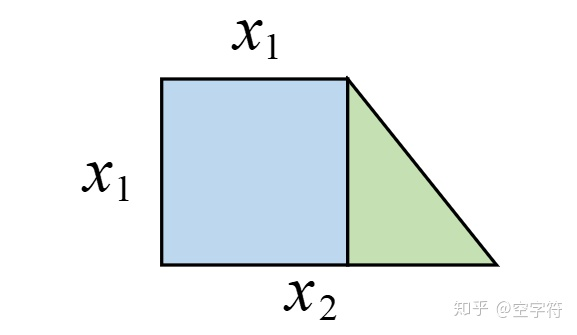
2.2 建模

用多特征线性回归建模也可以，但是不太好。​$h(x)=w_1{x}_1+w_2{x}_2+b$，毕竟我们学过梯形面积公式，需要有底边乘以高，仅仅只用多变量线性去拟合，估计不行，因为没交叉项和高次项。对于这个梯形：左边可以看成是正方形，所以可以人为的构造第三个特征$(x_1{)}^2$；而整体可以看成是长方形的一部分，又可以认为的构造出$x_1\ast x_2$；最后，整体还可以看成是大正方形的一部分，因此可以构造出$(x_2{)}^2$。故，我们便可以得到如下模型：

$h(x)=x_1{w}_1+x_2{w}_2+{\left(x_1\right)}^2{w}_3+x_1{x}_2{w}_4+{\left(x_2\right)}^2{w}_5+b$

这样特征比较多，有从左侧方形去计算的特征，有从长方形入手计算的特征，有人可能会问，有的部分重复加了，计算出来的面积岂不大于实际面积？但这当然不会，因为每一项都有一个权重参数[公式]做系数。同时，可以看出$h(x)$中包含了$x_1\ast x_2$，$(x_1{)}^2$，$(x_2{)}^2$这些项（其次数高于1），因此我们将其称之为多项式回归（Poloniumial Regression）。
但是，只要我们做如下替换，便又回到了普通的线性回归：
$h(x)=x_1{w}_1+x_2{w}_2+x_3{w}_3+x_4{w}_4+x_5{w}_5+b$
其中$x_3={\left(x_1\right)}^2,x_4=x_1{x}_2,x_5={\left(x_2\right)}^2$，只是在实际建模时我们先要将原始两个特征的数据转化为五个特征的数据；同时在做正式预测时，输入给模型$h(x)$也将是包含五个特征的数据。

2.3导入包并构造数据集

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

def make_data():
    np.random.seed(10)
    x1 = np.random.randint(5, 10, 50).reshape(50, 1)
    x2 = np.random.randint(10, 16, 50).reshape(50, 1)
    x = np.hstack((x1, x2))
    # 在这里我们便得到了一个50行2列的样本数据，
    #其中第一列为上底，第二列为下底
    y = 0.5 * (x1 + x2) * x1
    return x, y
    
x,y=make_data()

查看数据形式，x1，x2，y

x1=x[:,0]
x2=x[:,1]
ax = plt.subplot(projection = '3d')  # 创建一个三维的绘图工程
ax.set_title('3d_image_show')  # 设置本图名称
ax.scatter(x1, x2, y, c = 'r')   # 绘制数据点 c: 'r'红色，'y'黄色，等颜色
ax.set_xlabel('x1')  # 设置x1坐标轴
ax.set_ylabel('x2')  # 设置x2坐标轴
ax.set_zlabel('y')  # 设置y坐标轴

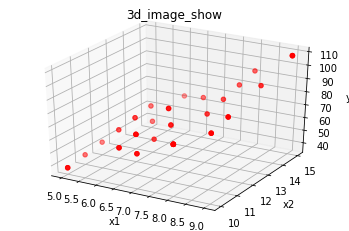
如果用平面​$h(x)=w_1{x}_1+w_2{x}_2+b$去拟合上图数据，其实不妥，最好用曲面。

求解数据，暂时只有x1、x2，建立交互项与高次方项，使用工具PolynomialFeatures()

poly = PolynomialFeatures(include_bias=False)#删除偏置项，这里加不加偏置项均可，最终计算回归模型时模型都会计算偏置项b。
x_mul = poly.fit_transform(x)

假设的公式，上面代码中偏置项没用上，所以x_mul为：
$xmul=x_1{w}_1+x_2{w}_2+{\left(x_1\right)}^2{w}_3+x_1{x}_2{w}_4+{\left(x_2\right)}^2{w}_5$

我们需要计算的是参数与偏置项，构建回归模型：

poly = PolynomialFeatures(include_bias=False)
x_mul = poly.fit_transform(x)
model = LinearRegression()
model.fit(x_mul, y)
print("权重为：", model.coef_)
print("偏置为：", model.intercept_)

求得权重为： [[-6.12180555e-15 4.55191440e-15 5.00000000e-01 5.00000000e-01
5.55111512e-17]]
偏置为： [-4.26325641e-14]
这里的-6.12180555e-15这种数据实在是太小，近乎0了。带入公式得：
$\begin{array}{rl}h(x)& =x_1\cdot 0+x_2\cdot 0+x_3\cdot 0.5+x_4\cdot 0.5+x_5\cdot 0+b\\ & =0.5\cdot {\left(x_1\right)}^2+0.5\cdot x_1\cdot x_2\\ & =0.5\cdot x_1\left(x_1+x_2\right)\end{array}$
至此，模型自己总结出了计算面积的公式，和我们已知的面积计算公式一致。

利用真实数据验证，例如：

print("上底 {}，下底 {}梯形真实面积：{}".format(5, 8, 0.5 * (5 + 8) * 5))
x_mul = poly.transform([[5, 8]])
print(x_mul)
print("上底 {}，下底为 {}梯形预测面积：{}".format(5, 8, model.predict(x_mul)))

上底 5，下底 8梯形真实面积：32.5
[[ 5. 8. 25. 40. 64.]]
上底 5，下底为 8梯形预测面积：[[32.5]]