Matlab基本命令练习

1.创建三维数组:

>> A4=[1,2;3,4]
>>A5=[5,6;7,8];
>> A6=cat(3,A4,A5)

结果：
A6(:,:,1) =

 1     2
 3     4

A6(:,:,2) =

 5     6
 7     8

2.利用reshape定义三维数组:

 reshape(1:12,[2,2,3])

结果:
ans(:,:,1) =

 1     3
 2     4

ans(:,:,2) =

 5     7
 6     8

ans(:,:,3) =

 9    11
10    12

3.利用cell函数定义元胞数组:

>> c2=cell(2,4)

c2 =

[]    []    []    []
[]    []    []    []

c2{2,3}=[1 2 3 4 5]

c2 =

[]    []              []    []
[]    []    [1x5 double]    []

4.数组转换函数

A1=rand(60,50);
B1=mat2cell(A1,[10 20 30],[25,25]) %将矩阵分块，转为元胞数组

B1 =

[10x25 double]    [10x25 double]
[20x25 double]    [20x25 double]
[30x25 double]    [30x25 double]

C1=cell2mat(B1);%将元胞数组转为矩阵
isequal(A1,C1)

ans =

 1

除此之外，还有几个常用的命令：
num2cell,将数值型数组转为元胞数组
cell2struct,将元胞型数组转为结构数组
struct2cell,将结构数组转为元胞数组
num2str,将数值型数组转为字符型数组
str2num,将字符型数组转为数值型数组

5.矩阵的点乘方不要求矩阵为方阵，有以下两种情况:
(1)A为矩阵，x为标量，A.^x表示对矩阵中的每一个元素求x次方；
(2)A和x为同型矩阵，A.^x表示对矩阵A中的每一个元素求x中对应元素次方。

6.(1)det()函数计算矩阵的行列式，inv()计算逆矩阵,pinv()可计算广义伪逆矩阵。
(2)eig()计算方阵的特征向量，trace()计算矩阵的迹，rank()计算矩阵的秩。

7.建立5×5矩阵A，A的第一行乘以1，第二行乘以2，…,第五行乘以5.

A=[12,13,14,15,13;44,54,56,23,54;98,54,12,67,45;44,65,12,76,23;54,23,76,32,90];
D=diag(1:5);
D*A

8.求矩阵上三角阵的函数是triu(A),triu(A,k)功能是提取矩阵第k条对角线以上的元素。同理，下三角矩阵的函数为tril()。将矩阵左右翻转的函数是fliplr(),上下反转为flipud()。

9.MATLAB绘制图形。

>> x=logspace(-1,2);
>> loglog(x,exp(x),'-s')
>> grid on
>> xlabel('X');
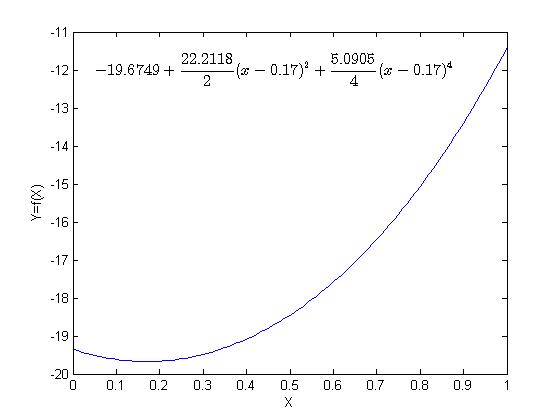
>> ylabel('Y');

画一个复杂的函数图像：

>> fun=@(a,x)[a(1)+a(2)/2*(x-0.17).^2+a(3)/4*(x-0.17).^4];
>> x=0:00.01:1;
>> y=fun(a,x);
>> xlabel('X');
>> ylabel('Y=f(X)');
>> text('Interpreter','latex',...
'String',['$$-19.6749+\frac{22.2118}{2}(x-0.17)^2'...
'+\frac{5.0905}{4}(x-0.17)^4$$'],'Position',[0.05,-12],...
'FontSize',12)

效果图：

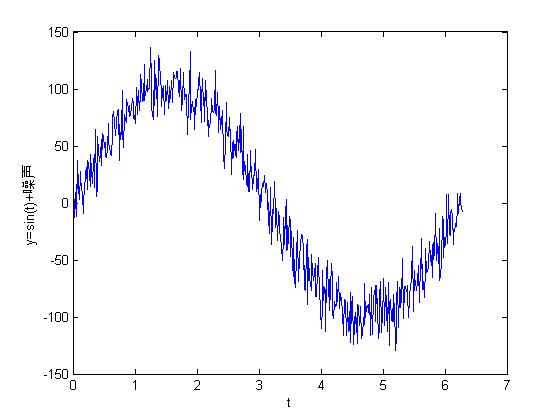
10.产生一列正弦波信号，然后调用smooth函数对加入的噪声进行滤波(平滑处理):

>> t=linspace(0,2*pi,500)';
>> y=100*sin(t);
>> noise=normrnd(1,15,500,1);
>> y=y+noise;
>> figure;
>> plot(t,y);
>> xlabel('t');
>> ylabel('y=sin(t)+噪声');
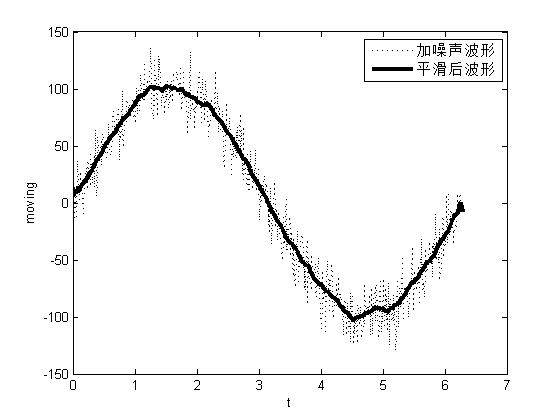
>> yy1=smooth(y,30);
>> figure;
>> plot(t,y,'k:');
>> hold on;
>> plot(t,yy1,'k','linewidth',3);
>> xlabel('t');
>> ylabel('moving');
>> legend('加噪声波形','平滑后波形');

效果图:

11.用不同方法求解f(x)的数值导数，并在坐标系中画出f’(x)的图像。

>> f=inline('sqrt(x.^3+2*x.^2-x+12)+(x+5).^(1/6)+5*x+2');
>> g=inline('(3*x.^2+4*x-1)./sqrt(x.^3+2*x.^2-x+12)/2+1/6./(x+5).^(5/6)+5');
>> x=-3:0.01:3;
>> p=polyfit(x,f(x),5);
>> dp=polyder(p);
>> dpx=polyval(dp,x);
>> dx=diff(f([x,3.01]))/0.01;
>> gx=g(x);
>> plot(x,dpx,x,dx,'.',x,gx,'-');

结果图：