互补集合模态分解

互补集合模态分解（complementary ensemble empirical mode decomposition）

参考文献：
Yeh, Jia-Rong, Jiann-Shing Shieh, and Norden E. Huang. “Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method.” Advances in Adaptive Data Analysis 2.02 (2010): 135-156.
下载链接：https://pdfs.semanticscholar.org/0eba/2c94147ea971be5cfbeaf13278ef0d61248a.pdf

CEEMD的提出

EMD分解常常因为混叠模态问题使这个分解出现问题，后来提出了EEMD，通过引入噪声来协助分析方法，平均值的思想很好地解决了混叠模态的问题（mode mixing）。然而，没有缺陷的东西是不存在的。由于引入噪声协助分析，集合求均值的处理过程复杂，便带来了计算复杂和耗时的问题；同时，噪声的引入对原始信号存在一定程度的破坏，而且引入的噪声会有残余。
互补集合模态分解（complementary ensemble empirical mode decomposition）时引入的是互补的噪声。这些噪声是独立同分布的，完美地负相关。由于引入的是互补噪声，所以在重构信号的时候冗余噪声很大程度上被消除。

噪声的产生和添加

使用下面的矩阵产生两个信号，其中S表示原始信号，N表示白噪声。M1表示添加了“正噪声”的混合信号，M2表示添加了“负噪声”的混合信号。

$${\left[\begin{array}{cc} M_1\\ M_2 \end{array}\right]}={ \left[ \begin{array}{cc} 1 & 1\\ 1 & -1 \end{array} \right ]}{ \left[ \begin{array}{cc} S\\ N \end{array} \right ]}$$

分解过程

CEEMD的分解过程与EEMD分解过程是相同的。区别在CEEMD要处理的信号有两个，添加了“正噪声”的混合信号M1，添加了“负噪声”的混合信号M2。 按照EMD分解的步骤分别将两个混合信号分解成两组本征模态函数（IMFs），然后让对应的每一阶本征模态函数（IMF）求集合平均值。该平均值就是最终所求的分解结果。

CEEMD的优点

（1）节省处理时间
（2）随着添加的噪声的数量增加，最终重构的数据中噪声的残余量减小，最终残余量几乎可以忽略。
（3）使用均方根误差（RMS error）比较EEMD和CEEMD时发现两者差别不大。

原始信号固有噪声的影响

由于CEEMD是一个噪声协助分析方法，需要添加噪声到信号中。如果信号本身的噪声已经足够大，那么再添加噪声对该方法会有什么影响就是现在要探究的问题。

决定信号的主要成分

蒙特卡罗(Monte Carlo)验证法可以根据本征模态函数的能量密度分布和平均周期确定其特性。
Wu 和 Huang提出了一种测试未知噪声等级的信号中真实信号含量的方法。通过这个测试，我们可以得到一个判断本征模态函数是有效信号主导的还是噪声主导的。

$$E_n=\frac{1}{N}\times{\sum_{j=0}^n |C_n(j)|^2}$$
$$\bar T_n=\int S_{lnT,n}dlnT(\int S_{lnT,n} \frac {dlnT}{T})^{-1}$$
$E_n$ 第n阶本征模态函数的能量密度；
$S_{lnT,n}$是第n阶本征模态函数的傅里叶频谱。
T是周期， $T_n$是是第n阶本征模态函数的平均周期。

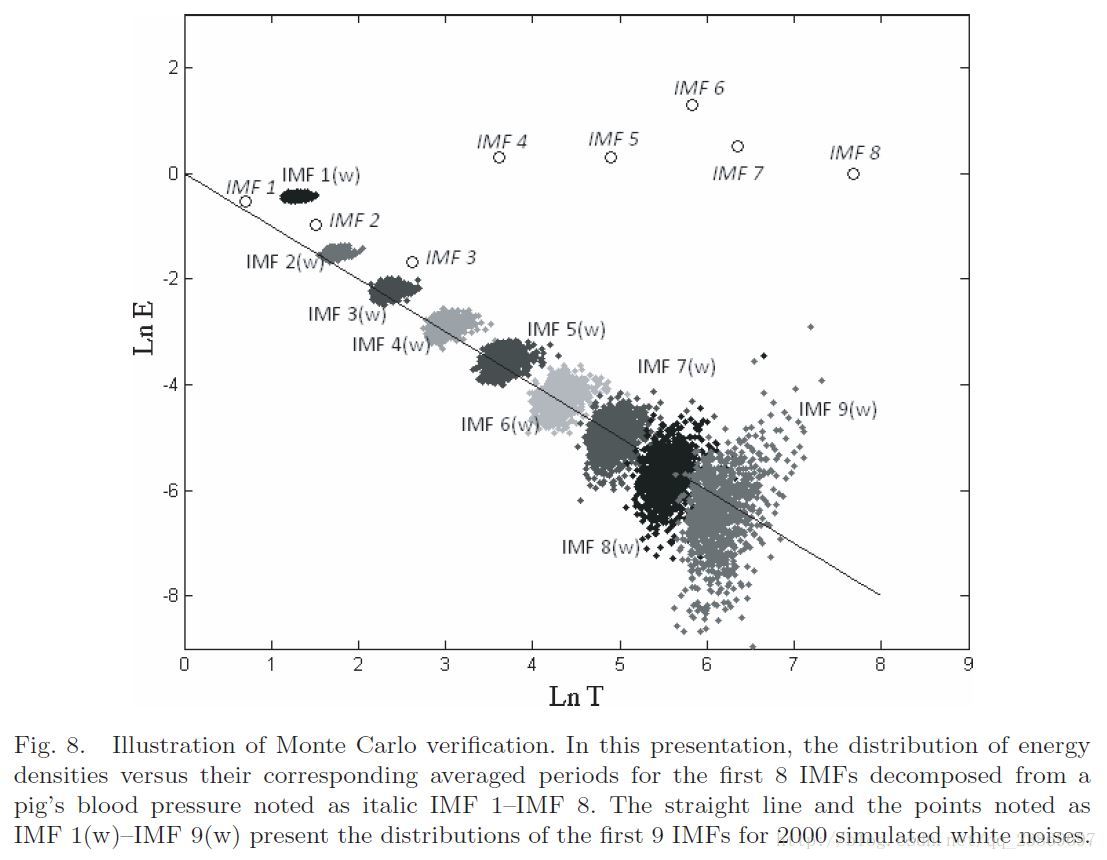
图8 是从原文截取的。在直线上的点被认为是噪声为主导的本征模态函数。 在重构信号时，丢弃这些函数使用剩余的函数进行重构。在重构的时候，为了进一步分开信号和噪声，先使用中值滤波消除起伏。

使用非稳态正弦信号作为仿真信号

未完