谱聚类（Spectral Clustering）算法介绍

最新推荐文章于 2025-03-20 11:19:41 发布

Y学习使我快乐V

最新推荐文章于 2025-03-20 11:19:41 发布

阅读量6.9w

点赞数 67

分类专栏：机器学习文章标签： Spectral Clustering 谱聚类

本文链接：https://blog.csdn.net/qq_24519677/article/details/82291867

版权

本文详细介绍了谱聚类的基本原理，包括谱的概念、谱聚类算法的步骤，以及拉普拉斯矩阵的重要属性。文章通过图论的角度，探讨了谱聚类与切图的关系，如最小切、RatioCut和Ncut。谱聚类的优势在于处理高维数据和非凸形状的聚类问题，但对相似度矩阵和参数选择敏感。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一. 前言

本来想写关于聚类系列算法的介绍，但是聚类系列的其它几个算法原理比较简单，网上有大量的教程可以查阅。这里主要是介绍一下谱聚类算法，做一个学习笔记，同时也希望对想要了解该算法的朋友有一个帮助。关于聚类的其他系列算法，这里推荐一个写的很不错的博客。

谱聚类在最近几年变得受欢迎起来，主要原因就是它实现简单，聚类效果经常优于传统的聚类算法（如K-Means算法）。刚开始学习谱聚类的时候，给人的感觉就是这个算法看上去很难，但是当真正的深入了解这个算法的时候，其实它的原理并不难，但是理解该算法还是需要一定的数学基础的。如果掌握了谱聚类算法，会对矩阵分析，图论和降维中的主成分分析等有更加深入的理解。

本文首先会简单介绍一下谱聚类的简单过程，然后再一步步的分解这些过程中的细节以及再这些过程中谱聚类是如何实现的，接着总结一下谱聚类的几个算法，再接着介绍谱聚类算法是如何用图论知识来描述，最后对本文做一个总结。下面我们就来介绍一下谱聚类的基本原理。

二. 谱聚类的基本原理介绍

2.1 谱和谱聚类

2.1.1 谱

方阵作为线性算子，它的所有特征值的全体统称为方阵的谱。方阵的谱半径为最大的特征值。矩阵A的谱半径是矩阵 $A^TA$ 的最大特征值。

2.1.2 谱聚类

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的母的。谱聚类可以理解为将高维空间的数据映射到低维，然后在低维空间用其它聚类算法（如KMeans）进行聚类。

2.2 谱聚类算法简单描述

输入：n个样本点 $X=\left \{ x{_{1}},x{_{2}},...,x{_{n}} \right \}$ 和聚类簇的数目k；

输出：聚类簇 $A{_{1}},A{_{2}},...,A{_{k}}$

（1）使用下面公式计算 n*n 的相似度矩阵W；

$s{_{ij}}=s(x{_{i}},x{_{j}})=\sum_{i=1,j=1}^{n}exp\frac{-||x{_{i}}-x{_{j}}||^2}{2\sigma ^2}$

W为 $s{_{ij}}$ 组成的相似度矩阵。

（2）使用下面公式计算度矩阵D；

$d{_{i}}=\sum_{j=1}^{n}w{_{ij}}$ ，即相似度矩阵W的每一行元素之和

D为 $d{_{i}}$ 组成的 n*n 对角矩阵。

（3）计算拉普拉斯矩阵 L=D-W ；

（4）计算L的特征值，将特征值从小到大排序，取前k个特征值，并计算前k个特征值的特征向量 $u{_{1}},u{_{2}},...,u{_{k}}$ ；

（5）将上面的k个列向量组成矩阵 $U=\left \{ u{_{1}},u{_{2}},...,u{_{k}} \right \}$ ， $U\in R^{n*k}$ ；

（6）令 $y{_{i}}\in R^k$ 是的第行的向量，其中 i=1,2,...,n ；

（7）使用k-means算法将新样本点 $Y=\left \{ y{_{1}},y{_{2}},...,y{_{n}} \right \}$ 聚类成簇 $C{_{1}},C{_{2}},...,C{_{k}}$ ；

（8）输出簇 $A{_{1}},A{_{2}},...,A{_{k}}$ ，其中， $A{_{i}}=\left \{ j|y{_{j}} \in C{_{i}}\right \}$ .

上面就是未标准化的谱聚类算法的描述。也就是先根据样本点计算相似度矩阵，然后计算度矩阵和拉普拉斯矩阵，接着计算拉普拉斯矩阵前k个特征值对应的特征向量，最后将这k个特征值对应的特征向量组成 n*k 的矩阵U，U的每一行成为一个新生成的样本点，对这些新生成的样本点进行k-means聚类，聚成k类，最后输出聚类的结果。这就是谱聚类算法的基本思想。相比较PCA降维中取前k大的特征值对应的特征向量，这里取得是前k小的特征值对应的特征向量。但是上述的谱聚类算法并不是最优的，接下来我们一步一步的分解上面的步骤，总结一下在此基础上进行优化的谱聚类的版本。

2.3 谱聚类算法中的重要属性

2.3.1 相似度矩阵介绍

相似度矩阵就是样本点中的任意两个点之间的距离度量，在聚类算法中可以表示为距离近的点它们之间的相似度比较高，而距离较远的点它们的相似度比较低，甚至可以忽略。这里用三种方式表示相似度矩阵：一是 $\epsilon$ -近邻法（ $\epsilon$ -neighborhood graph），二是k近邻法（k-nearest nerghbor graph），三是全连接法（fully connected graph）。下面我们来介绍这三种方法。

（1） $\epsilon$ -neighborhood graph：

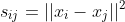$s{_{ij}}=||x{_{i}}-x{_{j}}||^2$ ，表示样本点中任意两点之间的欧式距离

用此方法构造的相似度矩阵表示如下：

$W{_{ij}}=\begin{cases} 0& \text{ if } s{_{ij}}>\epsilon \\ \epsilon & \text{ if } s{_{ij}}\leq \epsilon \end{cases}$

该相似度矩阵由于距离近的点的距离表示为 $\epsilon$ ，距离远的点距离表示为0，矩阵种没有携带关于数据集的太多的信息，所以该方法一般很少使用，在sklearn中也没有使用该方法。

（2）k-nearest nerghbor graph：

由于每个样本点的k个近邻可能不是完全相同的，所以用此方法构造的相似度矩阵并不是对称的。因此，这里使用两种方式表示对称的knn相似度矩阵，第一种方式是如果 $v{_{i}}$ 在 $v{_{j}}$ 的k个领域中或者 $v{_{j}}$ 在 $v{_{i}}$ 的k个领域中，则 $w{_{ij}}=w{_{ji}}$ 为 $v{_{i}}$ 与 $v{_{j}}$ 之间的距离，否则为<

最低0.47元/天解锁文章