机器学习技术（5）---- 最大期望算法Expectation-Maximum

一、模型证明基础

1.1 Jensen不等式：

如果函数f为凸函数，那么存在下列公式：

• f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)

若θ1,⋯,θk≥0,θ1+⋯+θk=1θ1,⋯,θk≥0,θ1+⋯+θk=1；则：

• f(θ1x1+⋯+θkxk)≤θ1f(x1)+⋯+θkf(xk)f(θ1x1+⋯+θkxk)≤θ1f(x1)+⋯+θkf(xk)
• f(E(x))≤E(f(x))f(E(x))≤E(f(x))
• 当且仅当 p(x=E(X))=1p(x=E(X))=1,即XX是常量时，等号成立

Jensen不等式应用于凹函数时，不等号方向反向。

1.2 EM 推导过程（离散值）

1. 给定的 m 个训练样本{x(1),x(2),⋯,x(m)}{x(1),x(2),⋯,x(m)}，样本间独立，找出样本模型参数θθ，极大化参数模型分布的对数似然函数如下：

• 对数似然函数：l(θ)=∑mi=1log(P(xi;θ))l(θ)=∑i=1mlog(P(xi;θ))

θ=argθmax∑mi=1log(P(xi;θ))θ=argθmax∑i=1mlog(P(xi;θ))

1. 假定样本数据中存在隐含数据z={z(1),z(2),⋯,z(k)}z={z(1),z(2),⋯,z(k)}，此时极大化模型分布的对数似然函数如下：

   θ=argθmax∑mi=1log(P(xi;θ))θ=argθmax∑i=1mlog(P(xi;θ))

   =argθmax∑mi=1log(∑z(i)P(z(i))P(x(i)|z(i);θ))=argθmax∑i=1mlog(∑z(i)P(z(i))P(x(i)|z(i);θ))

   =argθmax∑mi=1log(∑z(i)P(x(i),z(i);θ)=argθmax∑i=1mlog(∑z(i)P(x(i),z(i);θ)

2. 假设z的分布为Q(z;θ)Q(z;θ)，且∑zQ(z;θ)=1∑zQ(z;θ)=1，Q(z;θ)≥0Q(z;θ)≥0（如果z为连续性，那么Q是概率密度函数，需要将求和符号换成积分符号）；那么有如下公式：

• l(θ)=∑mi=1log(∑z(i)P(x(i),z(i);θ)l(θ)=∑i=1mlog(∑z(i)P(x(i),z(i);θ)
• =∑mi=1log(∑z(i)Q(z(i);θ)P(x(i),z(i);θ)Q(z(i);θ)=∑i=1mlog(∑z(i)Q(z(i);θ)P(x(i),z(i);θ)Q(z(i);θ)

1. 根据凹函数的Jensen不等式
   • l(θ)≥∑mi=1∑z(i)Q(z(i);θ)log(P(x(i),z(i);θ)Q(z(i);θ)l(θ)≥∑i=1m∑z(i)Q(z(i);θ)log(P(x(i),z(i);θ)Q(z(i);θ)
2. 根据Jensen不等式性质,且∑zQ(z;θ)=1∑zQ(z;θ)=1：
   • p(x,z;θ)Q(z,θ)=cp(x,z;θ)Q(z,θ)=c
   • ⇒Q(z;θ)=p(x,z;θ)c=p(x,z;θ)c∑zQ(z;θ)⇒Q(z;θ)=p(x,z;θ)c=p(x,z;θ)c∑zQ(z;θ)
   • =p(x,z;θ)∑zp(x,z;θ)=p(x,z;θ)∑zp(x,z;θ)
   • =p(x,z;θ)p(x;θ)=p(x,z;θ)p(x;θ)
   • =p(z|x;θ)=p(z|x;θ)
     • 从概率的角度而言，p(z|x;θ)p(z|x;θ)表示为在θ参数的模型中，在xi的条件下，取到zi的概率。
3. 将上式结果带入l(θ)l(θ)
   • l(θ)=∑mi=1log(∑z(i)p(z|x;θ)P(x(i),z(i);θ)p(z|x;θ)l(θ)=∑i=1mlog(∑z(i)p(z|x;θ)P(x(i),z(i);θ)p(z|x;θ)
   • θ=argθmaxl(θ)

1.3 最大似然估计

根据贝叶斯法则，我们可以通过条件概率P（x|w）和先验概率P（w）,计算得到后验概率P（w|x），那么这里有一个重要的假设条件就是：条件概率和先验概率都是已知的，但是很多情况下，先验概率和条件概率是未知的，而先验概率往往可以通过①训练样本中各类出现的频率估计；②经验；③每个样本所属的自然状态都是已知的（有监督学习）等途径获知.

但是对于条件概率而言，我们往往很难得到条件概率，这主要是由于：①条件概率密度函数包含了一个随机变量的全部信息，我们无法准确评估；②样本数据可能不多，或者缺失数据，导致我们无法估计；③特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度P（x|wi）转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。

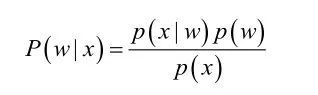
极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

 由于样本集中的样本都是独立同分布的，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：

那么，似然函数（linkehood function）：联合概率密度函数称为相对于的θ的似然函数。如下式：

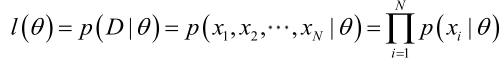
如果是参数空间中能使似然函数最大的θ值，则应该是“最可能”的参数值，那么 

就是θ的极大似然估计量。它是样本集的函数，记作：

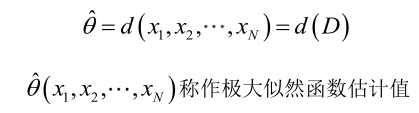
 那么，下面就进行到了求解似然函数的过程，也就是求解下面的式子：

 为了求解方便，两边取对数，得到：

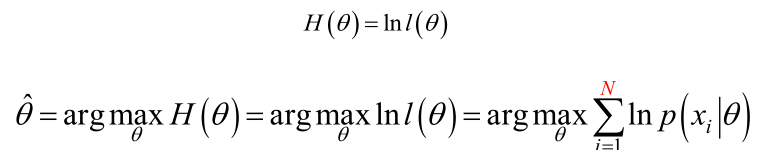
考虑到位置参数可能有多个，因此可以分为两类求解：

(1)未知参数只有一个（θ为标量）

        在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：

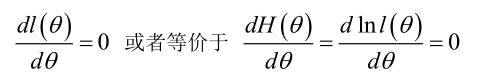
(2)未知参数有多个（θ为向量）

        则θ可表示为具有S个分量的未知向量：

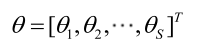
         记梯度算子：

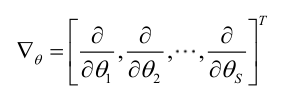
         若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。

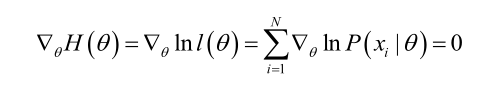
         尤其需要注意的是：样本的估计值仅仅是一个估计值，它是建立在一定的样本数据基础上的，只有在样本数趋于无限多的时候，它才会接近于真实值。

  最大似然估计的特点：

        1.比其他估计方法更加简单；

        2.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；

        3.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。

二、EM算法细节

上面的极大似然参数估计方法假设条件就是：样本数据是可以观测到的，如观测到样本数据服从正态分布，估计正态分布的两个参数，但是往往样本数据是不可能观测到的，里面含有不可观测的隐变量，这就需要用到EM方法。

 考虑带有隐变量 Z (观测值为 z )的参数估计问题。将观测数据（亦称不完全数据）记为 Y=(y1,...,yN)Y=(y1,...,yN) ，不可观测数据记为 Z=(z1,...,zN)Z=(z1,...,zN) ， Y 、Z 合在一起称为完全数据。那么观测数据的似然函数为：

为了方便求解，仍然转换为对数似然函数：

所有的证明过程可以通过上面获得。

也就是说类似于似然估计方法，EM方法仍然是要求极值的，但是所不同的是，EM算法是迭代算法，通过迭代的方式求取目标函数 L(θ)=lnP(Y|θ)L(θ)=ln⁡P(Y|θ) 的极大值。因此，希望每一步迭代之后的目标函数值会比上一步迭代结束之后的值大。设当前第 nn 次迭代后参数取值为 θnθn ，我们的目的是使 L(θn+1)>L(θn)L(θn+1)>L(θn) 。那么考虑：

 使用琴生不等式（Jensen inequality）：

 

 

 那么，就可以得到下面的EM算法过程：

 因此，EM算法的原理是似然估计方法和迭代求解方法的结合，其关键点在于下面

①参数预计过程中，某些是可以观测到的变量（比如投币过程中的投币结果可以观测到），某一些是不可以直接观测到的（投币的过程），但是不可观测的变量存在可能性的取值。见下面的这一个例子：

假设有三枚硬币A、B、C，这些硬币正面出现的概率分别是 ππ 、pp 、qq 。进行如下掷硬币试验： 先掷A，如果A是正面则再掷B，如果A是反面则再掷C。对于B或C的结果，如果是正面则记为1，如果是反面则记为0。进行 NN 次独立重复实验，得到结果。现在只能观测到结果，不能观测到掷硬币的过程，估计模型参数 θ=(π,p,q)θ=(π,p,q) 。        在这个问题中，实验结果是可观测数据 Y=(y1,...,yN)Y=(y1,...,yN) ，硬币A的结果是不可观测数据 Z=(z1,...,zN)Z=(z1,...,zN) 且 zz 只有两种可能取值1和0。

②E和M两个迭代过程一定要计算准确。

上面的许多内容参考了下面的这篇文章，感谢大佬。

Determined22 - 博客园