SVM技术详解(下)

最新推荐文章于 2024-05-26 09:49:55 发布

Taolla

最新推荐文章于 2024-05-26 09:49:55 发布

阅读量413

点赞数

分类专栏：数据文章标签： svm 技术

数据专栏收录该内容

9 篇文章 0 订阅

订阅专栏

1. 对偶问题

m a x 1 | | w | | s . t ., y i (w' x i + b) \geq 1, i = 1, . . ., n

$max \frac{1}{||w||} s.t.,y_i(w'x_i+b)\ge1,i=1,...,n$

m i n 1 2 | | w | | 2 s . t ., y i (w' x i + b) \geq 1, i = 1, . . ., n

$min\frac{1}{2}||w||^2 s.t.,y_i(w'x_i+b)\ge1,i=1,...,n$

现在的目标函数是二次的，约束条件是线性的，所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。

二次规划的一般形式：

$min x q (x) = 1 2 x' G x + x' c$ $\min_{x} q(x)=\frac{1}{2}x'Gx+x'c$ $s . t . a' i x \geq b i$ $s.t. a_i'x\ge b_i$
其中 $G是$ Hessian矩阵， $\tau$ 是有限指标集， $c$ ， $x$ 和 $a_i$ ，都是R中的向量。如果Hessian矩阵是半正定的，则我们说 $（1.1）$ 是一个凸二次规划，在这种情况下该问题的困难程度类似于线性规划（如果结果为0，二次规划问题就变成线性规划问题了）。如果有至少一个向量满足约束并且在可行域有下界，则凸二次规划问题就有一个全局最小值。如果是正定的，则这类二次规划为严格的凸二次规划，那么全局最小值就是唯一的。如果是一个不定矩阵，则为非凸二次规划，这类二次规划更有挑战性，因为它们有多个平稳点和局部极小值点。

通过给每一个约束条件加上一个拉格朗日乘子（Lagrange multiplier） $\alpha$ ，定义拉格朗日函数（通过拉格朗日函数将约束条件融合到目标函数里）：

ζ (w, b, a) = 1 2 | | w | | 2 - \sum i = 0 n a i (y i (w' x i + b) - 1)

$\zeta(w,b,a)=\frac{1}{2}||w||^2-\sum_{i=0}^n a_i(y_i(w'x_i+b)-1)$

θ (w) = max a i \geq 0 ζ (w, b, a)

$\theta(w)=\max_{a_i\ge0} \zeta(w,b,a)$
容易验证，当某个约束条件不满足时，例如

yi(w′xi+b)<1 $y_i(w'x_i+b)\lt1$ ,那么显然有

θ(x)=∞ $\theta(x)=\infty$ (只要令

ai=∞ $a_i=\infty$ 即可）。而当所有条件都满足时，则最优解为

θ(w)=12||w||2 $\theta(w)=\frac{1}{2}||w||^2$ ，亦即最初要最小化的量。

min w, b = min w, b max a i \geq 0 ζ (w, b, a) = p *

$\min_{w,b}=\min_{w,b}\max_{a_i\ge0} \zeta(w,b,a)=p^*$
这里用

p∗ $p^*$ ，表示这个问题的最优值，且和最初的问题是等价的。如果直接求解，那么一上来便得面对

w $w$ 和

b $b$ 两个参数，而

αi $\alpha_i$ 又是不等式约束，这个求解过程不好做。不妨把最小和最大的位置交换一下，变成：

max a i \geq 0 min w, b ζ (w, b, a) = d *

$\max_{a_i\ge0}\min_{w,b} \zeta(w,b,a)=d^*$
交换以后的新问题是原始问题的对偶问题，这个新问题的最优值用

d∗ $d^*$ 来表示。而且有

d∗≤p∗ $d^*\le p^*$ ,在满足某些条件的情况下，这两者相等.

2. KTT条件

凸优化的概念： $\chi \subset R^n$ 为一凸集， $f:\chi \to R$ 为一凸函数。凸优化就是要找出一点 $x^*\in \chi$ 使得每一 $x \in \chi$ ，满足 $f(x^*) \le f(x)$ .
KKT条件的意义：它是一个非线性规划（Nonlinear Programming）问题能有最优化解法的必要和充分条件。

原始问题通过满足KKT条件，已经转化成了对偶问题。而求解这个对偶学习问题，分为3个步骤：首先要让 $\zeta(w，b，a)$ 关于 $w$ 和 $b$ 最小化，然后求对的极大，最后利用SMO算法求解对偶问题中的拉格朗日乘子。

3. 线性不可分的推广——引进核函数Kernel

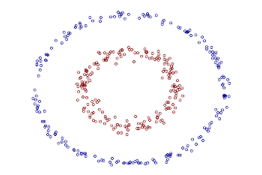
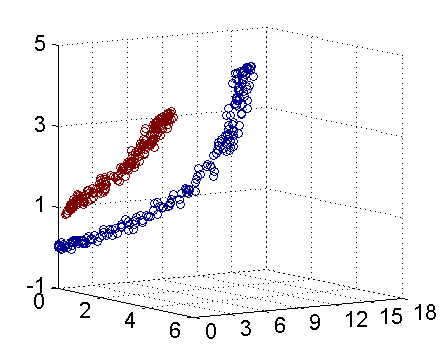
在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开，如下图所示的两类数据，分别分布为两个圆圈的形状，这样的数据本身就是线性不可分的，此时该如何把这两类数据分开呢
kernel

如果我们做一个映射 $\phi:R2 \to R5$ ，将 $X$ 按照上面的规则映射为 $Z$ ，那么在新的空间中原来的数据将变成线性可分的，从而使用之前我们推导的线性分类算法就可以进行处理了。
通过引进从输入空间 $X$ 到另一个高维的 Hilbert 空间 $H$ 的变换将原输入空间 $\lambda$ 的训练集:

T = {(x 1, y 1), (x 2, y 2), . . ., (x l, y l)} \in (X \times Y) l

$T= \{ (x_1,y_1),(x_2,y_2),...,(x_l,y_l)\} \in(X \times Y)^l$
转化为 Hilbert 空间

H $H$ 中的新的训练集：

T ¯ = {(x ¯ 1, y 1), (x ¯ 2, y 2), . . ., (x ¯ l, y l)} = {(θ (x 1), y 1), (θ (x 2), y 2), . . ., (θ (x l), y l)}

$\bar T= \{ (\bar x_1,y_1),(\bar x_2,y_2),...,(\bar x_l,y_l)\}=\{ (\theta(x_1),y_1),(\theta(x_2),y_2),...,(\theta(x_l),y_l)\}$

使其在 Hilbert 空间 $H$ 中线性可分， Hilbert 空间 $H$ 也称为特征空间。然后在空间 $H$ 中求得超平面 $(\omega *\phi(x))+b=0$ ，这个超平面可以硬性划分训练集 T <script type="math/tex" id="MathJax-Element-7511">T</script> ，于是原问题转化为如下的二次规划问题
convert