假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10. 试为这8个字母设计赫夫曼编码.

哈夫曼编码

【问题描述】

假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10. 试为这8个字母设计赫夫曼编码.(要求构造的赫夫曼树中除叶子节点之外的所有节点的左孩子的节点值小于右孩子的节点值)

【输入形式】

输入n=8，输入8个字母；输入按序8个字母出现的频率

【输出形式】

输出编码后的哈夫曼树（先序或者完全二叉树序）

【样例输入】

8
abcdefgh
0.07
0.19
0.02
0.06
0.32
0.03
0.21
0.10

【样例输出】

The a 's Huffman code is:1010
The b 's Huffman code is:00
The c 's Huffman code is:10000
The d 's Huffman code is:1001
The e 's Huffman code is:11
The f 's Huffman code is:10001
The g 's Huffman code is:01
The h 's Huffman code is:1011

代码部分

#include<iostream>
using namespace std;
#include<cstdio>
#include<cstring>
typedef struct node {   //哈夫曼树中单个节点的信息
	int parent;   //父节点
	char letter;   //字母
	int lchild;
	int rchild;
	double weight;   //权值
}*HuffmanTree;
void Select(HuffmanTree& tree, int n, int& s1, int& s2) {   //找到权值最小的两个值的下标，其中s1的权值小于s2的权值
	int min = 0;
	for (int i = 1; i <= n; i++) {
		if (tree[i].parent == 0) {
			min = i;
			break;
		}
	}
	for (int i = min + 1; i <= n; i++) {
		if (tree[i].parent == 0 && tree[i].weight < tree[min].weight)
			min = i;
	}
	s1 = min;   //找到第一个最小值，并赋给s1
	for (int i = 1; i <= n; i++) {
		if (tree[i].parent == 0 && i != s1) {
			min = i;
			break;
		}
	}
	for (int i = min + 1; i <= n; i++) {
		if (tree[i].parent == 0 && i != s1 && tree[i].weight < tree[min].weight)
			min = i;
	}
	s2 = min;  //找到第二个最小值，并赋给s2
}
void CreateHuff(HuffmanTree& tree, char* letters, double* weights, int n) {
	int m = 2 * n - 1;   //若给定n个数要求构建哈夫曼树，则构建出来的哈夫曼树的结点总数为2n-1
	tree = (HuffmanTree)calloc(m + 1, sizeof(node));   //开辟空间顺序储存Huffman树，用calloc开辟的空间初始化的值为0（NULL），符合Huffman树初始化条件（parent、weight、lchild、rchild等初始化应为0），由于tree[0]不存数据（因为任何节点的父节点若为0，会与节点初始化0值相混淆，故不存数据），则要开辟（2n-1）+1个空间（额外开辟一个空间）
	for (int i = 1; i <= n; i++) {   //给节点赋字母及其对应的权值
		tree[i].weight = weights[i - 1];
		tree[i].letter = letters[i];
	}
	for (int i = n + 1; i <= m; i++) {
		int s1 = 0, s2 = 0;
		Select(tree, i - 1, s1, s2);   //每次循环选择权值最小的s1和s2,生成它们的父结点
		tree[i].weight = tree[s1].weight + tree[s2].weight;   //新创建的节点i 的权重是s1和s2的权重之和
		tree[i].lchild = s1;   //新创建的节点i 的左孩子是s1
		tree[i].rchild = s2;   //新创建的节点i 的右孩子是s2
		tree[s1].parent = i;   //s1的父亲是新创建的节点i
		tree[s2].parent = i;   //s2的父亲是新创建的节点i
	}   //Huffman树创建完毕
    //------------打印哈夫曼树中各结点之间的关系（仅供测试使用，上传cg需注释掉此段代码）----------
	/*printf("---------------------------------------\n");
	printf("Huffman树为：\n");
	printf("下标   权值     父节点   左孩子   右孩子\n");
	printf("0\n");
	for(int i=1;i<m+1;i++){
		printf("%-4d   %-6.2lf   %-4d   %-4d   %-4d\n", i, tree[i].weight, tree[i].parent, tree[i].lchild, tree[i].rchild);
	}
	printf("---------------------------------------\n");
	cout << endl;*/
	//------------打印哈夫曼树中各结点之间的关系（仅供测试使用，上传cg需注释掉此段代码）----------
}
void HuffmanCoding(HuffmanTree& tree, char**& HuffCode, int n) {
	HuffCode = (char**)malloc(sizeof(char*) * (n + 1));   //运用char型二级指针，可理解成包含多个char*地址的数组，开n+1个空间，因为下标为0的空间不用
	char* tempcode = (char*)malloc(sizeof(char) * n);
	tempcode[n - 1] = '\0';
	for (int i = 1; i <= n; i++) {
		int start = n - 1;	
		int doing = i;   //doing为正在编码的数据节点
		int parent = tree[doing].parent;   //找到该节点的父结点
		while (parent) {   //直到父结点为0(NULL)，即父结点为根结点时停止
			if (tree[parent].lchild == doing)   //如果该结点是其父结点的左孩子，则编码为0，否则为1
				tempcode[--start] = '0';
			else 
				tempcode[--start] = '1';
			doing = parent;   //继续往上进行编码
			parent = tree[parent].parent;
		}
		HuffCode[i] = (char*)malloc(sizeof(char) * (n - start));   //开辟用于存储编码的内存空间
		strcpy(HuffCode[i], &tempcode[start]);   //将编码拷贝到字符指针数组中的相应位置
	}
	free(tempcode); //释放辅助空间
}
int main() {
	int n = 0;
	cin >> n;   //输入数据个数
	char* letters = (char*)malloc(sizeof(char) * (n + 1));
	for (int i = 1; i <= n; i++)
		cin >> letters[i];
	double* weights = (double*)malloc(sizeof(double) * n);
	for (int i = 0; i < n; i++)
		cin >> weights[i];
	HuffmanTree tree;
	CreateHuff(tree, letters, weights, n);   //构建哈夫曼树
	char** HuffCode;
	HuffmanCoding(tree, HuffCode, n);
	for (int i = 1; i <= n; i++)
		printf("The %c 's Huffman code is:%s\n", tree[i].letter, HuffCode[i]);
	return 0;
}

此解法运用了char型二级指针，此题也可作为二级指针的运用实例。

哈夫曼树的基本概念

在认识哈夫曼树之前，你必须知道以下几个基本术语：

1、什么是路径？

在一棵树中，从一个结点往下可以达到的结点之间的通路，称为路径。

如图，从根结点A到叶子结点I的路径就是A->C->F->I

2、什么是路径长度？

某一路径所经过的“边”的数量，称为该路径的路径长度

如图，该路径经过了3条边，因此该路径的路径长度为3

3、什么是结点的带权路径长度？

若将树中结点赋给一个带有某种含义的数值，则该数值称为该结点的权。从根结点到该结点之间的路径长度与该结点的权的乘积，称为该结点的带权路径长度。

如图，叶子结点I的带权路径长度为 3 × 3 = 9 3\times3=93×3=9

4、什么是树的带权路径长度？

树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

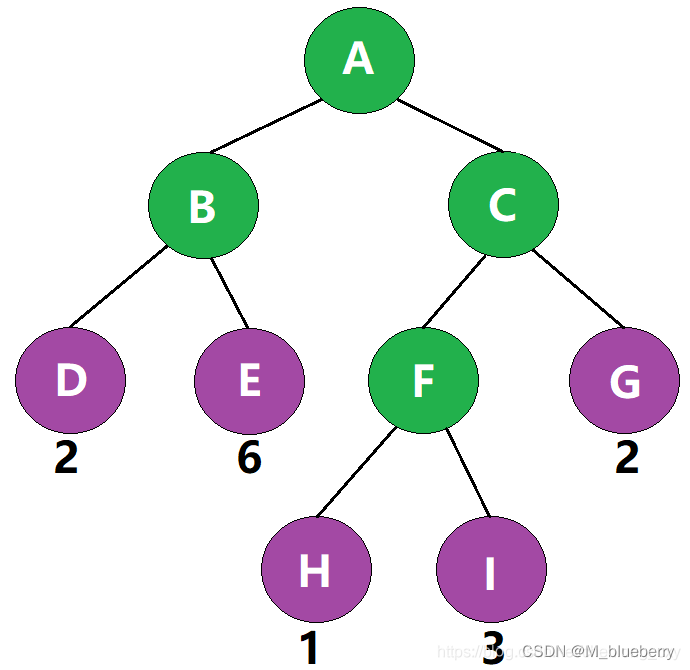
如图，该二叉树的带权路径长度 WPL= 2 × 2 + 2 × 6 + 3 × 1 + 3 × 3 + 2 × 2 = 32

5、什么是哈夫曼树？

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，则称该二叉树为哈夫曼树，也被称为最优二叉树。

根据树的带权路径长度的计算规则，我们不难理解：树的带权路径长度与其叶子结点的分布有关。
即便是两棵结构相同的二叉树，也会因为其叶子结点的分布不同，而导致两棵二叉树的带权路径长度不同。
那如何才能使一棵二叉树的带权路径长度达到最小呢？
根据树的带权路径长度的计算规则，我们应该尽可能地让权值大的叶子结点靠近根结点，让权值小的叶子结点远离根结点，这样便能使得这棵二叉树的带权路径长度达到最小。

哈夫曼树的构建

构建思路

下面给出一个非常简洁易操作的算法，来构造一棵哈夫曼树：
 1、初始状态下共有n个结点，结点的权值分别是给定的n个数，将他们视作n棵只有根结点的树。
 2、合并其中根结点权值最小的两棵树，生成这两棵树的父结点，权值为这两个根结点的权值之和，这样树的数量就减少了一个。
 3、重复操作2，直到只剩下一棵树为止，这棵树就是哈夫曼树。
我们还可以发现，哈夫曼树不存在度为1的结点。因为我们每次都是选择两棵树进行合并，自然不存在度为1的结点。
由此我们还可以推出，若给定n个数要求构建哈夫曼树，则构建出来的哈夫曼树的结点总数为2n-1，因为对于任意的二叉树，其度为0的叶子结点个数一定比度为2的结点个数多1。