两个向量叉乘（定义是类似多项式相乘再求和）和点乘（定义是对应位置的坐标相乘再求和）的定义和证明，以及和四元数乘法的联系和区别。

哈密顿是单位长度的三个方向微分。散度的结果没有IJK（I*I=1特性）是标量

向量叉乘：

两个向量的坐标量积又叫做向量积，用于计算法向量。

游戏内应用：

用于判断物体在自身的左右方位。

还有应用于图形学里，对环境光照于自身顶点或者片元的法向量的夹角来判断光漫反射的强弱。

用于相机视图是否剔除该面的渲染。

等等。

判断方式

图片是截取自百度百科https://baike.baidu.com/item/%E5%90%91%E9%87%8F%E7%A7%AF/4601007?fr=aladdin

顺时针方向从b旋转到a，使用左手定则，四指方向是旋转方向，大拇指方向即为法向量方向。

逆时针方向从a到b，可使用右手定则，上同。

法向量的模定义为：

也就是ab平行四边形面积。

证明

为了更好地推导，我们需要加入三个轴对齐的单位向量i，j，k。

i，j，k满足以下特点：

i=jxk；j=kxi；k=ixj；

kxj=–i；ixk=–j；jxi=–k；

ixi=jxj=kxk=0；（0是指0向量）

由此可知，i，j，k是三个相互垂直的向量。它们刚好可以构成一个坐标系。

这三个向量的特例就是i=（1，0，0）j=（0，1，0）k=（0，0，1）。

对于处于i，j，k构成的坐标系中的向量u，v我们可以如下表示：

u=Xu*i+Yu*j+Zu*k；

v=Xv*i+Yv*j+Zv*k；

那么uxv=（Xu*i+Yu*j+Zu*k）x（Xv*i+Yv*j+Zv*k）

=Xu*Xv*（ixi）+Xu*Yv*（ixj）+Xu*Zv*（ixk）+Yu*Xv*（jxi）+Yu*Yv*（jxj）+Yu*Zv*（jxk）+Zu*Xv*（kxi）+Zu*Yv*（kxj）+Zu*Zv*（kxk）

由于上面的i，j，k三个向量的特点，所以，最后的结果可以简化为

uxv=（Yu*Zv–Zu*Yv）*i+（Zu*Xv–Xu*Zv）*j+（Xu*Yv–Yu*Xv）*k。 [1]

https://baike.baidu.com/item/%E5%90%91%E9%87%8F%E7%A7%AF/4601007?fr=aladdin

要计算向量积，我们需要引用几个公式

代数规则

1、反交换律：a×b=-b×a

2、加法的分配律：a×（b+c）=a×b+a×c。

3、与标量乘法兼容：（ra）×b=a×（rb）=r（a×b）。

4、不满足结合律，但满足雅可比恒等式：a×（b×c）+b×（c×a）+c×（a×b）=0。

5、分配律，线性性和雅可比恒等式别表明：具有向量加法和叉积的R3构成了一个李代数。

6、两个非零向量a和b平行，当且仅当a×b=0

且当我们设坐标系三个单位向量为i，j，k可得：

比百度百科更清晰的证明为了更好地推导，我们需要加入三个轴对齐的单位向量i，j，k。

i，j，k满足以下特点：

i=jxk；j=kxi；k=ixj；

kxj=–i；ixk=–j；jxi=–k；

ixi=jxj=kxk=0；（0是指0向量）

由此可知，i，j，k是三个相互垂直的向量。它们刚好可以构成一个坐标系。

关于ijk的特点应该和四元数中ijk三个量中的彼此两两相乘等于-1有联系的2023.3.10

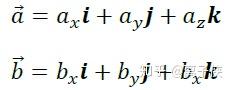
根据以上几个代数规则可得

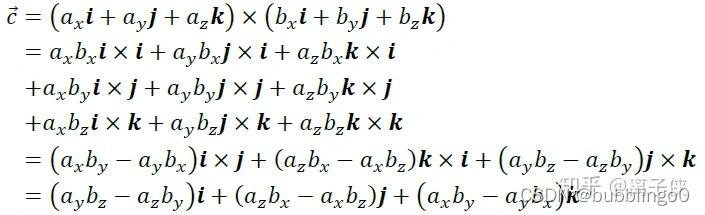
则a×b=[a2b3-a3b2，a3b1-a1b3，a1b2-a2b1]

————————————————

版权声明：本文为CSDN博主「bubblingo0」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/qq_39329287/article/details/121847740

两个向量的点积

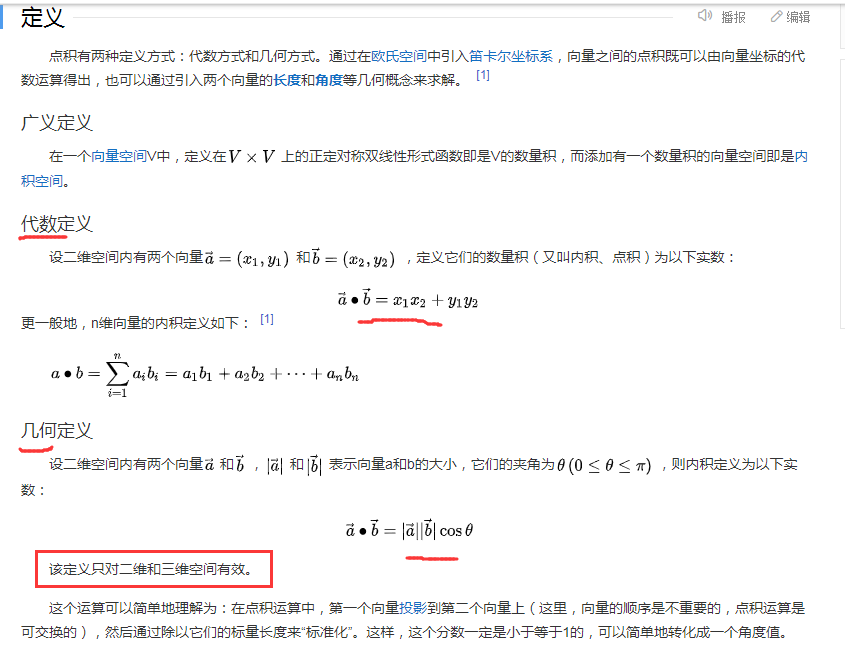
点积在数学中，又称数量积（dot product; scalar product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。 [1]

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：

a·b=a1b1+a2b2+……+anbn。

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

a·b=（a^T）*b，这里的a^T指示矩阵a的转置。

https://baike.baidu.com/item/%E7%82%B9%E7%A7%AF/9648528?fromModule=lemma_inlink

======点乘======

推导公式1:

a•b = ax*bx + ay*by

= (|a|*sinθ1) * (|b| * sinθ2) + (|a| * cosθ1) * (|b| * cosθ2)

= |a||b|(sinθ1*sinθ2 + cosθ1*cosθ2)

=|a||b|(cos(θ1-θ2))

= |a||b|cosθ

推导公式2:

几何意义是：算角度，算投影

======叉乘======:

几何意义是:算方向,算面积

为什么叉乘能代表方向 因为叉乘是 a X b = |a||b|sinθ,（原因是叉乘结果平行四边形面积） 点乘的 a . b = |a||b|conθ（原因是点乘结果a在b的投影再和a相乘）

https://blog.csdn.net/weixin_30363817/article/details/101945982