机器学习 —— 神经网络（matlab）

最新推荐文章于 2025-03-13 16:41:43 发布

洋洋菜鸟

最新推荐文章于 2025-03-13 16:41:43 发布

阅读量2w

点赞数 20

分类专栏：机器学习文章标签：神经网络数据预测体育数据训练算法模型验证

本文链接：https://blog.csdn.net/qq_25990967/article/details/125067858

版权

一、介绍

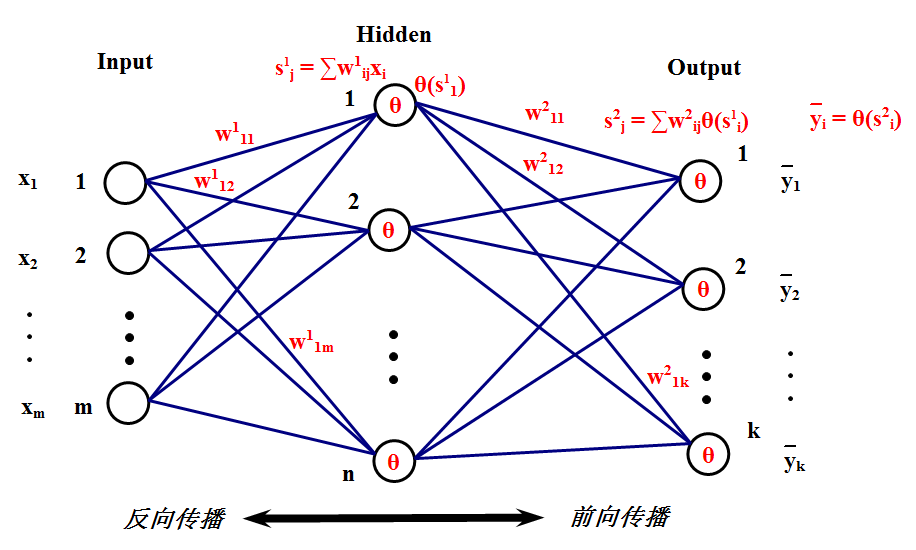
神经网络是一种运算模型，由大量的节点（或称“神经元”，或“单元”）和之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。人工神经网络通常是通过一个基于数学统计学类型的学习方法（Learning Method）得以优化，所以人工神经网络也是数学统计学方法的一种实际应用，通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间，另一方面在人工智能学的人工感知领域，我们通过数学统计学的应用可以来做人工感知方面的决定问题(也就是说通过统计学的方法，人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力)，这种方法比起正式的逻辑学推理演算更具有优势。

二、实验数学原理

三、实验算法和实验步骤

步骤：

1.准备训练网络的样本，并对数据进行标准化处理。

2.初始化网络的参数，包括最大训练次数，隐含层神经元数量，网络学习速率，训练的目标误差

3.对训练集样本进行训练，找到拟合模型

4.用该模型对训练集进行预测

5.对训练集的预测结果进行还原

6.对训练集的预测结果进行验证

7.用模型对对预测集进行预测

8.对预测集的结果进行还原并输出

四、实例分析

数据来源：

样本	跳高成绩(m)	30行进跑(s)	立定三级跳远(m)	助跑摸高(m)	助跑4—6步跳高(m)	负重深蹲杠铃(kg)	杠铃半蹲系数	100(s)	抓举(kg)
序号
1	2.24	3.2	9.6	3.45	2.15	140