HDU 1506 Largest Rectangle in a Histogram 动态规划

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 16137    Accepted Submission(s): 4735

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

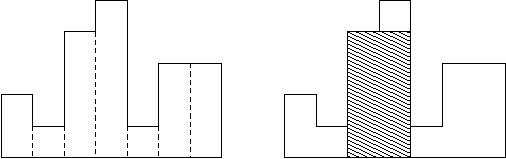
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

Sample Input

  
  

   
   7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
  
  

 

Sample Output

  
  

   
   8
4000
  
  

 

Source

University of Ulm Local Contest 2003

 

Recommend

LL

 

    题意：柱状图中n个柱体，求最大的连续的矩形的面积，单调栈类型题目。题目很容易看懂，不赘述。

    分析：很容易理解，求取每个数的左右能够延展到达区间并记录，最后遍历所得最大的结果即可。问题的关键是求取左右延展区间的过程，遍历肯定很耗时间，可使用动态规划处理。

    理解：当确认左边界时，如果它相邻左边数大于它，那么左边的数能到达的延展边界，该数也能够到达，直接跳至左边数的延展区间的下标所指的数的左边一个数重复过程即可，这样可以大大缩短时间。同理，当确认右边界时，如果相邻的右边数大于它，那么右边数可到达的范围该数也能够到达，跳至右边数右边区间所指下标数的右一个数再进行判断。左右边界数组需要初始化，且需要标记a[0]和a[n+1]为-1防止数组出界导致死循环。其他具体可根据代码理解。

    见AC代码：

#include<stdio.h>
#include<algorithm>
#define  ll long long
using namespace std;
const int maxn=100005;
ll a[maxn];
int l[maxn],r[maxn];
int main()
{
	int  n;
	while(~scanf("%d",&n))
	{
		if(!n)
			break;
		for(int i=1; i<=n; i++)
		{
			scanf("%I64d",&a[i]);
			l[i]=i;
			r[i]=i;
		}
		a[0]=a[n+1]=-1;
		for(int i=2; i<=n; i++)
		{
			while(a[i]<=a[l[i]-1])
				l[i]=l[l[i]-1];
		}
		for(int i=n-1; i>0; i--)
		{
			while(a[i]<=a[r[i]+1])
				r[i]=r[r[i]+1];
		}
		ll res=0;
		for(int i=1; i<=n; i++)
			res=max(res,(r[i]-l[i]+1)*a[i]);
		printf("%I64d\n",res);
	}
}

    最关键的还是得多敲多练，不要急于求成。打好基础方是正道。

    特记下，以备后日回顾。