《统计学习方法（第2版）》李航第十章隐马尔可夫模型思维导图笔记及课后习题答案（使用python3编写算法）

ML--小小白

于 2022-04-17 19:51:46 发布

阅读量2k

点赞数 1

分类专栏：统计学习方法笔记文章标签： python 人工智能机器学习

本文链接：https://blog.csdn.net/qq_26928055/article/details/124235031

版权

统计学习方法笔记专栏收录该内容

26 篇文章 20 订阅

订阅专栏

《统计学习方法（第2版）》李航第十章隐马尔可夫模型思维导图笔记

10.1

import numpy as np
from collections import Counter

A = np.array([[0.5, 0.2, 0.3],
              [0.3, 0.5, 0.2], 
              [0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5],
              [0.4, 0.6], 
              [0.7, 0.3]])
pi = np.array([[0.2, 0.4, 0.4]]).reshape(-1, 1)
O = np.array([0.0, 1.0, 0.0, 1.0]).reshape(-1, 1)  # red: 0.0; white: 1.0
M = len(Counter(O.flatten()))
N = len(A)
T = len(O)
beta = np.zeros((T, N))

# 迭代法给出后向概率的值
def backward_prob(t, i, T, A, B, O):
    N = len(A)
    if t==T-1:
        return 1.0
    elif t<=(T-1):
        result = A[i] * B[:, int(O[t+1])]
        for j in range(N):
            result[j] *= backward_prob(t+1, j, T, A, B, O)
        return result.sum()
    else:
        print('backward_prob with error')

# 计算后向概率矩阵：
for t in range(T):
    for i in range(N):
        beta[t, i] = backward_prob(t, i, T, A, B, O)

# 最终的序列出现概率为：
(pi.flatten() * B[:, int(O[0])] * beta[0, :]).sum()

0.06009079999999999

beta

array([[0.112462, 0.121737, 0.104881],
       [0.2461  , 0.2312  , 0.2577  ],
       [0.46    , 0.51    , 0.43    ],
       [1.      , 1.      , 1.      ]])

beta矩阵为后向概率矩阵，其中的第t行第i列的含义为，t时刻，为i态的后向概率。

10.2

请添加图片描述

A = np.array([[0.5, 0.1, 0.4],
              [0.3, 0.5, 0.2], 
              [0.2, 0.2, 0.6]])
B = np.array([[0.5, 0.5],
              [0.4, 0.6], 
              [0.7, 0.3]])
pi = np.array([[0.2, 0.3, 0.5]]).reshape(-1, 1)
O = np.array([0, 1, 0, 0, 1, 0, 1, 1]).reshape(-1, 1)  # red: 0.0; white: 1.0
M = len(Counter(O.flatten()))
N = len(A)
T = len(O)
beta = np.zeros((T, N))  # 后向概率矩阵
alpha = np.zeros((T, N)) # 前向概率矩阵
gamma = np.zeros((T, N)) # 某时刻处于某状态的概率矩阵，参见书10.2.4节

# 迭代法给出前向概率的值
# 返回的是t+1时刻的前向概率
def forward_prob(t, i, T, A, B, pi, O):
    N = len(A)
    if t==0:
        return pi[i] * B[i, int(O[0])]
    elif 0<t<T:
        result = A[:, i] * B[i, int(O[t])]
        for j in range(N):
            result[j] = result[j] * forward_prob(t-1, j, T, A, B, pi, O)
        return result.sum()
    else:
        print('froward_prob with error')

# 迭代法给出后向概率的值
def backward_prob(t, i, T, A, B, O):
    N = len(A)
    if t==T-1:
        return 1.0
    elif t<T:
        result = A[i] * B[:, int(O[t+1])]
        for j in range(N):
            result[j] *= backward_prob(t+1, j, T, A, B, O)
        return result.sum()
    else:
        print('backward_prob with error')

# 计算前向概率矩阵：
for t in range(T):
    for i in range(N):
        alpha[t, i] = forward_prob(t, i, T, A, B, pi, O)

# 计算后向概率矩阵：
for t in range(T):
    for i in range(N):
        beta[t, i] = backward_prob(t, i, T, A, B, O)

beta

array([[0.00632569, 0.00684706, 0.00577855],
       [0.01482964, 0.01227214, 0.01568294],
       [0.02556442, 0.02343448, 0.02678985],
       [0.04586531, 0.05280909, 0.04280618],
       [0.105521  , 0.100883  , 0.111934  ],
       [0.1861    , 0.2415    , 0.1762    ],
       [0.43      , 0.51      , 0.4       ],
       [1.        , 1.        , 1.        ]])

alpha

array([[0.1       , 0.12      , 0.35      ],
       [0.078     , 0.084     , 0.0822    ],
       [0.04032   , 0.026496  , 0.068124  ],
       [0.0208668 , 0.01236192, 0.04361112],
       [0.0114321 , 0.01019392, 0.01109573],
       [0.00549669, 0.00338373, 0.00928834],
       [0.00281056, 0.00245952, 0.00253453],
       [0.00132502, 0.00121063, 0.00094105]])

# 计算gamma矩阵
gamma = alpha * beta
gamma = gamma / gamma.sum(axis=1, keepdims=True)

# 要求的即为gamma矩阵的第4行3列的元素
gamma[3, 2]

0.5369518160647323

10.3

在习题10.1中，试用维特比算法求最优路径

A = np.array([[0.5, 0.2, 0.3],
              [0.3, 0.5, 0.2], 
              [0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5],
              [0.4, 0.6], 
              [0.7, 0.3]])
pi = np.array([[0.2, 0.4, 0.4]]).reshape(-1, 1)
O = np.array([0.0, 1.0, 0.0, 1.0]).reshape(-1, 1)  # red: 0.0; white: 1.0
M = len(Counter(O.flatten()))
N = len(A)
T = len(O)
beta = np.zeros((T, N))

上面已知条件取自10.1

# 定义最优路径最大概率矩阵和最优路径状态矩阵
delta = np.zeros((T, N))
psi = np.zeros((T, N))

# 最优路径最大概率迭代计算
def optimal_loop_prob(t, i, A, B, O, pi, T):
    N = len(A)
    if t==0:
        return pi[i] * B[i, int(O[0])], 0
    elif 0<t<T:
        result1 = A[:, i] * B[i, int(O[t])]
        for j in range(N):
            result1[j] *= optimal_loop_prob(t-1, j, A, B, O, pi, T)[0]
        result2 = result1.argmax()
        result1 = result1[result2]
        return result1, result2
    else:
        print('optimal_loop_prob with error')

# 计算最优路径最大概率矩阵和最优路径状态矩阵
for t in range(T):
    for i in range(N):
        delta[t, i] = optimal_loop_prob(t, i, A, B, O, pi, T)[0]
        psi[t, i] = optimal_loop_prob(t, i, A, B, O, pi, T)[1]

# 找到总体最优路径,及末尾时刻最优路径中的状态
optimal_loop_probability = delta[T-1, :].max()
optimal_loop_final_state = delta[T-1, :].argmax()

# 回溯最优路径中各个时刻的状态
optimal_loop_states = [optimal_loop_final_state]
for t in np.arange(T-2, -1, -1):
    state = psi[t+1, int(optimal_loop_states[-1])]
    optimal_loop_states.append(state)
optimal_loop_states.reverse() # 将顺序变为从初始时刻到T时刻
print(f'最优状态序列：{optimal_loop_states}')

最优状态序列：[2.0, 1.0, 1.0, 1]

注意这里三种状态分别为0态、1态和2态。

看一下最优路径的概率：

optimal_loop_probability

0.0030239999999999993

10.4

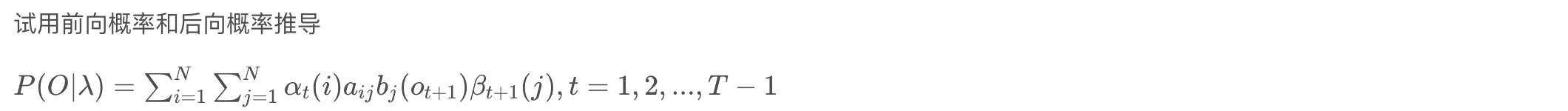
请添加图片描述

证明：
$\begin{aligned} P(O \mid \lambda) &=P\left(o_{1}, o_{2}, \ldots, o_{T} \mid \lambda\right) \\ &=\sum_{i=1}^{N} P\left(o_{1}, \ldots, o_{t}, I_{t}=q_{i} \mid \lambda\right) P\left(o_{t+1}, \ldots, o_{T} \mid I_{t}=q_{i}, \lambda\right) \\ &=\sum_{i=1}^{N} \sum_{j=1}^{N} P\left(o_{1}, \ldots, o_{t}, I_{t}=q_{i} \mid \lambda\right) P\left(o_{t+1}, I_{i+1}=q_{j} \mid I_{t}=q_{i} \lambda\right) P\left(o_{t+2}, \ldots, o_{T} \mid I_{t+1}=q_{j}, \lambda\right) \\ &=\sum_{i=1}^{N} \sum_{j=1}^{N} P\left(o_{1}, \ldots, o_{t}, I_{t}=q_{i} \mid \lambda\right) P\left(o_{t+1} \mid I_{i+1}=q_{j}, \lambda\right) P\left(I_{t+1}=q_{j} \mid I_{t}=q_{i}, \lambda\right) P\left(o_{t+2}, \ldots, o_{T} \mid I_{t+1}=q_{j}, \lambda\right) \\ &=\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{t}(i) a_{i j} b_{j}\left(o_{t+1}\right) \beta_{t+1}(j), \quad t=1,2, \ldots, T-1 \end{aligned}$

10.5

比较维特比算法中变量 $\delta$ 的计算和前向算法中变量 $\alpha$ 的计算的主要区别.

单纯从计算上，每一步递归， $\alpha$ 都涉及之前时刻自身的求和运算，而 $\delta$ 是求最大值运算。这也是容易理解的，以为 $\alpha$ 计算的是造成t时刻前面所有观测序列的可能性，因此有相对于状态的求和，而 $\delta$ 求的是最佳路径，其要考虑前面观测序列得到过程中，最可能经历的一组状态序列，因此要遍历状态来求最值，因此其实也容易知道，同一时刻， $\delta$ 一定是比 $\alpha$ 小的。

ML--小小白

关注

1
点赞
踩
5

收藏

觉得还不错? 一键收藏
打赏
0
评论
《统计学习方法（第2版）》李航第十章隐马尔可夫模型思维导图笔记及课后习题答案（使用python3编写算法）

10.1import numpy as npfrom collections import CounterA = np.array([[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]])B = np.array([[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]])pi = np.array([[0.2, 0..
复制链接

扫一扫